两条直线的位置关系

A卷

一、选择题

1、直线A₁x + B₁y + C₁ = 0，(A₁B₁≠0)与直线A₂x + B₂y + C₂ = 0，(A₂B₂≠0)垂直的充要条件是(　　　 )

A、C₁ C₂≠0　　　B、A₁B₁+ A₂B₂= 0　　 C、A₁ A₂+ B₁ B₂= 0　　 D、A₁ B₂－A₂ B₁= 0

2、两直线斜率相等是两直线平行的(　　　 )

A、充分不必要条件　　　　　　　　　　 B、必要不充分条件

C、充分必要条件　　　　　　　　　　 D、即不充分也不必要条件　

3、直线l₁：x + my + 6 = 0和直线l₂：(m－2)x + 3y + 2m = 0互相平行，则m的取值为(　　　 )

A、－1或3　　　B、－1　　　　 C、－3　　　　D、－1或－3

4、点A(a，b) 关于直线l：x－y = 0的对称点是(　　　 )

A、(－a，－b)　　　B、(a，－b)　　　C、(b，a)　　　　D、(－b，－a)

5、点M(3，－2)到直线2x + 3y +5 = 0的距离是(　　　 )

A、5　　　　　 B、　　　　C、　　　　 D、

6、两直线x²－xy－6y² = 0所夹的锐角是(　　　 )

A、30⁰　　　　 B、45⁰　　　　 C、60⁰　　　　 D、135⁰

7、两条直线3x+ 2y + n = 0和2x－3y + 1 = 0的位置关系是(　　　 )

A、平行　　　 B、垂直　　　 C、相交但不垂直　　　 D、与n的值有关

二、填空题

8、已知直线x + ky + 2 = 0经过两直线3x + 2y －9 = 0和x －1 = 0的交点，则k的值等于　　　　　。

9、两条平行线3x + 4y－12 = 0和6x + 8y + 11 = 0的距离是　　　　　　。

10、过原点的直线与直线的夹角为30⁰，则其方程是　　　　　　　　。

11、直线ax + by + 4 = 0过(－1，1)且与直线(a－1)x + y + b = 0垂直，则a = 　　　，

b = 　　　　　。

12、直线x + my + 6 = 0与(m－2)x + 3y + m = 0相交，则m的范围是　　　　　　。

13、直线mx + 10y = 3与3x + (n－1)y = －1 重合，则m = 　　　　，n = 　　　　　。

三、解答题

14、求垂直于3x－4y = 7且与两坐标轴围成的三角形周长为10的直线方程。

15、求经过点A (－2，2)且在第二象限与两坐标轴围成的三角形面积最小时的直线方程。

16、两平行线l₁，l₂分别过P₁(1，0)与P₂(0，5)，若l₁与l₂的距离为5，求两条直线的方程。

17、已知二次方程x² + xy－6y²－20x－20y + k = 0表示两条直线，试求k的值与两条直线的方程。

18、直线l过点P(3，4)，并且l在两坐标轴上截距相等，求直线l的方程。

B卷

一、综合题

1、求过点A(2，3)，且被两条平行直线3x + 4y－7 = 0和3x + 4y + 8 = 0截得长为的线段的直线方程。

2、已知直线l₁：x + my + 6 = 0，l₂：(m－2)x + 3y + 2m = 0,m取何值时：

(1) l₁ 与l₂相交；　　 (2) l₁ ⊥l₂；　　 (3) l₁ ∥l₂；　　　(4) l₁ 与l₂重合。

3、求过两直线l₁：y = 和l₂：3x－y = 0的交点，并且与原点距离为1的直线方程。

4、以直线l：x + 2y + 1 = 0为对称轴，求与直线l₁：x－y－2 = 0对称的直线l₂的方程。

二、应用题

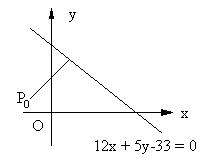5、如图所示，一个动点P(x,y)以P₀(－2,1)为起点,以v = 2m／s的速度沿着直线12x + 5y－33 = 0垂直的方向向着直线作匀速运动,求P点运动路线的方程,并求出到达给定直线所需时间.

三、创新题

6、将直线l沿x轴正向平移3个单位，沿y轴正向平移5个单位，得直线l＇，再将l＇沿x轴正向平移1个单位，沿y轴负向平移2个单位，恰与l重合。

(1)求直l＇与l之间距离；

(2)当l＇与l关于点(2,3)对称时，求l的方程。

四、高考题

7、如果直线ax + 2y + 2 = 0与直线3x－y－2 = 0平行，那么系数a = (　　 )

A、－3　　　　 B、－6　　　　 C、　　　　 D、

8、根据指令(机器人在平面上能完成下列动作:先原地旋转角度为(为正时,按逆时针方向旋转,为负时,按顺时针方向旋转－)，再朝其面对的方向沿直线行走距离r。

(1)现机器人在直角坐标系的坐标原点，且x轴正方向，试给机器人下一个指令，使其移动到点(4.4)。

(2)机器人在完成该指令后，发现在点(17,0)处有一小球正向坐标原点作匀速直线滚动，已知小球滚动速度为机器人行走的确倍，若忽略机器人原地旋转所需的时间，问机器人最快在何处截住小球？共给也机器人截住小球所需的指令（结果精确到小数点后两位）.

9、正方形中心为G(－1,0)，一边民在的直线斜率为3，且正方形的面积为14．4，求此正方形各边所在直线的方程。

参考答案

A卷

一、选择题

1、C　　2、D　　 3、B　　　4、C　　　5、B　　　6、B　　　7、B

二、填空题

8、－1　　 9、3．5　　 10、　　11、2，－2或－2，－6

12、m≠3且m≠－1　　 13、－9，　　

三、解答题

14、4x + 3y±10 = 0　　

15、x－y + 4 = 0

16、l1、l2的方程分别为y = 0，y = 5或5x－12y－5 = 0，5x－12y + 60 = 0

17、x + 3y－8 = 0、x－2y－12 = 0

18、x + y－7= 0，4x－3y = 0

B卷

一、综合题

1、7x + y－17 = 0和x－7y + 19 = 0

2、(1)当

　 (2)

　 (3)l₁∥l₂

(4)

3、x = 1或4x－3y + 5 = 0

4、7x－y－8 = 0

二、应用题

5、2（s）

三、创新题

6、( 1 )距离为　　　　 ( 2 )方程为6x－8y + 1 = 0

四、高考题

7、B　　　8、( 1 )指令为　　 ( 2 )指令为

9、正方形四边的所在直线为y = 3x－3，y = 3x + 9，x + 3y－5 = 0，x + 3y + 7 = 0