聊城市第一学期期中联考高二数学试题
考生注意:请将本试题的第一大题的答案填在答题卡上,其余答案全部按规定位置写在答卷纸上,最后只交答卷和答题卡.时间:100分钟,满分120分.
一、选择题(本题共12个小题,每小题5分,共60分.正确答案唯一)
1.预测人口的变化趋势有多种方法,“直接推算法”使用的公式是![]() ,
,![]() ,其中
,其中![]() 为预测期人口数,
为预测期人口数,![]() 为初期人口数,
为初期人口数,![]() 为预测期内年增长率,
为预测期内年增长率,![]() 为预测期间隔年数.如果在某一时期有
为预测期间隔年数.如果在某一时期有![]() ,那么在这期间人口数( )
,那么在这期间人口数( )
A.呈上升趋势 B.呈下降趋势 C.摆动变化 D.不变
2.在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,则△
,则△![]() 的面积为( )
的面积为( )
A.9 B.![]() C.
C.![]() D.
D.![]()
3.若![]() ,
,![]() ,
,![]() 成等比数列,则函数
成等比数列,则函数![]() 的图象与
的图象与![]() 轴的交点个数是( )
轴的交点个数是( )
A.0个 B.1个 C.2个 D.0个或2个
4.在数列![]() 中
中![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A.49 B
5. △![]() 中,若
中,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.若![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
高二数学试题(共4页)第1页
7. △![]() 中,
中,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.在等比数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.10
B
9.设![]() 是等差数列
是等差数列![]() 的前n项和,若
的前n项和,若![]() ,则
,则![]() 等于( )
等于( )
A.-1
B![]()
10.若不等式![]() 的解集是
的解集是![]() ,则
,则![]() 的值为( )
的值为( )
A.-10
B.
11.某电脑用户计划使用不超过400元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要,软件至少买3片,磁盘至少买2盒,则不同的选购方式共有( )
A.2种 B.3种 C.4种 D.5种
12.已知锐角三角形的边长分别是3、5、![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本题共4个小题,每小题4分,共16分)
13.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做这个数列的公和.已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为4,那么
,公和为4,那么![]() 的值为________,这个数列的前项和
的值为________,这个数列的前项和![]() 的计算公式为____________.
的计算公式为____________.
高二数学试题(共4页)第2页
14.设![]() ,请把
,请把![]() ,
,![]() ,从大到小的顺序排列起来_________.
,从大到小的顺序排列起来_________.
15.在△![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 所对的边,若
所对的边,若![]()
![]() ,
,![]() ,则
,则![]() _________.
_________.
16.已知![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的取值范围是_________.
的取值范围是_________.
三、解答题(本题共4个小题,共44分.解答应写出文字说明、证明过程或推演步骤)
17.(本小题满分10分)
2003年,伊拉克战争初期,美英联军为了准确分析战场形势,由分别位于科威特和沙特的两个相距为![]() 的军事基地
的军事基地![]() 和
和![]() ,测得伊拉克两支精锐部队分别在
,测得伊拉克两支精锐部队分别在![]() 处和
处和![]() 处,且
处,且![]() ,
,![]() ,
,![]() ,
,![]() ,如图所示,求伊军这两支精锐部队的距离.
,如图所示,求伊军这两支精锐部队的距离.

18. (本小题满分10分)
不等式![]() 对任意实数
对任意实数![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
19. (本小题满分12分)
要将两种大小不同的钢板截成![]() 、
、![]() 、
、![]() 三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
高二数学试题(共4页)第3页
| 规格类型 钢板类型 |
|
|
|
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
今需要![]() 、
、![]() 、
、![]() 三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需的三种规格成品,且使所用钢板张数最少?
三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需的三种规格成品,且使所用钢板张数最少?
20. (本小题满分12分)
已知数列![]() 满足
满足![]() ,
,![]() .
.
(1)是否存在一个常数![]() ,使数列
,使数列![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(2)若要使![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
聊城市2005----2006学年度第一学期期中联考
高二数学参考答案及评分标准
一、选择题(本题共12小题,每小题5分,共60分)
1.A 2.D 3.C 4.C 5.C 6.D 7.B 8.D 9.B 10.B 11.B 12.C
二、填空题(本题共4小题,每小题4分,共16分)
13.
2, 2n ; 14. ![]() ; 15. 2; 16.
; 15. 2; 16.![]()
三、解答题(共44分)
17.解:∵![]() 且
且![]()
∴![]()
∴![]() ………………2分
………………2分
在![]() 中,
中,![]()
由正弦定理得 ![]()
又∵![]()
∴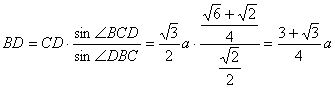 ………………6分
………………6分
在![]() 中,由于弦定理得
中,由于弦定理得
![]()
![]()
∴![]() ………………8分
………………8分
∴伊军这两支精锐部队的距离为![]() . ………………10分
. ………………10分
高二数学答案(共3页)第1页
18.解:(1)当![]() 时,
时,![]() 或
或![]() .
.
若![]() ,则原不等式变为
,则原不等式变为![]() ,显然对任意实数
,显然对任意实数![]() 都成立.
都成立.
若![]() ,则原不等式变为
,则原不等式变为![]() ,即
,即![]() ,显然对任意实数
,显然对任意实数![]() 不都成立.
不都成立.
∴ ![]() ………………4分
………………4分
(2)当![]() 时
时
∵关于![]() 的不等式
的不等式![]() ,对任意实数
,对任意实数![]() 都成立
都成立
∴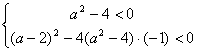 解之得
解之得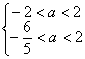
∴![]() ………………8分
………………8分
综上可得:![]() ………………10分
………………10分
19.解:设需截第一种钢板![]() 张,第二种钢板
张,第二种钢板![]() 张,总钢板数为
张,总钢板数为![]() 张. ………………2分
张. ………………2分
则有 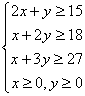 ,且
,且![]() 、
、![]() 都是整数
都是整数
目标函数为 ![]() =
=![]() +
+![]() ………………4分
………………4分
做出可行域如图所示,
平移直线![]() =
=![]() +
+![]() 可知直线经过可行域上的点
可知直线经过可行域上的点![]() 时,截距
时,截距![]() 最小,即
最小,即![]() 最小.
最小.
解方程组
![]() 得
得![]() .
.
但![]() 与
与![]() 都不是整数,所以可行解
都不是整数,所以可行解![]() 不是该问题的最优解. …………8分
不是该问题的最优解. …………8分
高二数学答案(共3页)第2页
描出点![]()
![]() 附近的横、纵坐标均为整数的所有点,将这些点的坐标分别代入约束条件及目标函数,经验证可知,在点
附近的横、纵坐标均为整数的所有点,将这些点的坐标分别代入约束条件及目标函数,经验证可知,在点![]() 和点
和点![]() 处
处![]() 取得最小值为12.
取得最小值为12.
∴当![]() 或
或![]() 时,
时,![]() . ………………10分
. ………………10分
由此可知,第一种截法是截第一种钢板3张、第二种钢板9张;第二种截法是截第一种钢板4张、第二种钢板8张.两种方法均最少要截两种钢板共12张. ……………12分
20.解:
(1)假设存在常数![]() ,使数列
,使数列![]() 是等比数列. ………………2分
是等比数列. ………………2分
则有 ![]()
即![]()
解得 ![]() ………………4分
………………4分
又∵![]()
∴当![]() 时,数列是
时,数列是![]() 首项为2,公比为
首项为2,公比为![]() 的等比数列. ……………6分
的等比数列. ……………6分
(2)由(1)知,![]()
∴![]() ………………8分
………………8分
由![]() 得
得 ![]()
即![]()
∴![]() ………………10分
………………10分
∴![]()
∴![]()
所以![]() 的取值范围是
的取值范围是![]() 且
且![]() ………………12分
………………12分
注:其它解答方法请参考答案给以相应分数.
高二数学答案(共3页)第3页
高二数学试题(共4页)第4页