哈五中2005-2006年度上学期期末

高二数学试卷

　 2006　1　10

说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120分钟。

第Ⅰ卷（选择题　共60分）

一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1．若a>b，则下列不等式（1）a+c>b+c；（2）a－c>b－c；（3）ac>bc；（4）>（c>0）其中恒成立的不等式个数为　　  （　 ）

（A）0　　　 （B）1　　　 （C）2　　　 （D）

2. 过点（1，0），且与直线平行的直线方程是(　　)

　 （A） 　　　　　（B）

　 （C）　　　　　  （D）

3.到两点A（-3，0）、B（3，0）距离之差的绝对值等于6的点的轨迹是（　　）

 （A）椭圆　　（B）线段 　　　 （C）双曲线  　　 （D）两条射线

4. 抛物线的准线方程是（　　）

（A）　　（B）　（C）　（D）

5. 圆= 25在x 轴上截得的弦长是（　　　）

　　 （A）3　 　 （B）4　　  （C）6　　　（D）8．

6与不等式同解的不等式为　 （　　 ）

（A）　　　　　 （B）

（C）lg>0　 （D）

7. 离心率为，一个焦点是（5，0）的双曲线的标准方程是（　 ）

　 （A）　　　　　　　 （B）　

　 （C）　　　　　　　 （D）

8. 已知两点M（1，-1），N（1，1），则M关于N的对称点的坐标是(　　)

　　 （A）（1，0）　　 （B）（1，2）　 　（C）（1，3） 　　　（D）（1，-3）

9. 不等式组表示的区域是(　　)

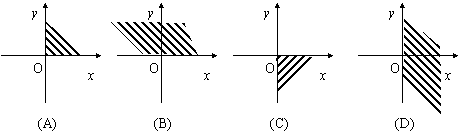10. 以点A（1，3），B（－2，8），C（7，5）为顶点的ABC是

　　A．直角三角形　　　　　　　　　 B．锐角三角形

　　C．钝角三角形　　　　　　　　　 D．等腰三角形

11. 已知椭圆 上有一点P，它到椭圆左准线的距离是，点P到右焦点的距离是它到左焦点距离的几倍(　　)

（A）7 　　　（B）6（C）5 　　　 （D）

12.、方程表示的曲线是 (　　)

A　抛物线的一段　　  B　线段　C  圆的一部分　　 D　抛物线

哈五中2005-2006上学期期末高二试卷

高二数学试卷答题纸

第Ⅰ卷答题卡

题号	1	2	3	4	5	6	7	8	9	10	11	12
选项

第Ⅱ卷（非选择题　共90分）

二、填空题（本大题共4小题，每小题4分，共16分。把答案填在题中横线上）

13. 函数（x＞0）的最小值为　　　　  ；

14．过点C（-1，1）和D（1，3），圆心在X轴上的圆的方程

为　　　　　　　　　　  。

15.已知F₁、F₂是椭圆+y²=1的两个焦点, P是该椭圆上的一个动点, 则PF₁·PF₂的最大值是　　　　　　 .

16  如图，抛物线形拱桥的顶点距水面2米时，测得拱桥内水面宽为12米，当水面升高1米后，拱桥内水面宽度是　　　　 。

三、解答题（本大题共6小题，共74分，解答题应写出文字说明、证明过程或演算步骤）

17. （本题满分12分）

解不等式　

18　. （本题满分12分）

在平面直角坐标系x O y中，△ABC的顶点B， C的坐标分别为（-3，0），（3，0），若△ABC的周长为16，则顶点A的轨迹方程

19. （本题满分12分）

（1）求过点A（1，－4），且与直线平行的直线方程

（2）求过点A（1，－4），且与直线垂直的直线方程

20. （本题满分12分）

求过点A（-3，2）的抛物线的标准方程。

21.（本题满分12分）

双曲线C 与椭圆 有公共焦点，且离心率 e =2 .

（1）　　　 求双曲线 C 的方程；

（2）　　　 直线  与双曲线 C  相交于 A、B 两点，求AB的弦长。.

22.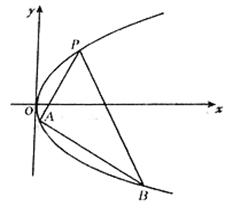（本题满分14分）如图，过抛物线y²=2px (p>0) 上一定点P(x₀, y₀) (y₀>0)，作两条直线分别交抛物线于A(x₁,y₁)，B(x₂,y₂).

（I）求该抛物线上纵坐标为的点到其焦点F的距离；　　　

（II）当PA与PB的斜率存在且倾斜角互补时，

求的值，并证明直线AB的斜率是非零常数。

哈五中2005-2006上学期期末高二试卷

高二数学试卷答案

第Ⅰ卷答题卡

题号	1	2	3	4	5	6	7	8	9	10	11	12
选项	D	A	D	B	D	D	D	C	C	C	C	A

第Ⅱ卷（非选择题　共90分）

二、填空题

13. 12；14． (x-2)²+y²=10 15. 4 16   

17　解不等式　 

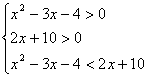
19（1） 解：∵的斜率为

　　　　∴所求直线方程为：

　　　　即　　　

　　（2）　 解：∵的斜率为

　　　　∴所求直线方程为：

　　　　即

20解：当抛物线的焦点在y轴的正半轴上时，

把A（-3，2）代入x²=2py，得p=

当焦点在x轴的负半轴上时，把A（-3，2）代入

得p=∴抛物线的标准方程为

21．解: (1)由已知得

椭圆方程为∴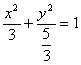

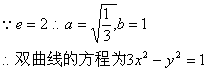
（2）由3x²-y²+1

　　　  x-y+1=0

得x²-x-1=0

∴x₁+x₂=1。x₁x₂=-1

AB=

22解：（I）当y=时，x=，又抛物线y²=2px

的准线方程为x=－，由抛物线定义得，所以

距离为.

（II）设直线PA的斜率为k_PA，直线PB的斜率为k_PB.

由=2px₁，=2px₀相减得　

　（y₁－y₀）(y₁+y₀)=2p(x₁－x₀)

故 k_PA=　（x₁≠x₀）同理可得k_PB=（x₂≠x₀）由PA，PB

倾斜角互补知k_PA=－k_PB，即=－，所以y₁+y₂=－2y₀，故

设直线AB的斜率为k_AB. 由=2px₂，=2px₁相减得（y₂－y₁）(y₂+y₁)=2p(x₂－x₁)，

所以k_AB=（x₁≠x₂）将 y₁+y₂=－2y₀　 (y₀>0 )代入得k_AB=

=－，所以k_AB是非零常数.