江苏省东海县海陵中学2005~2006学年度第一学期期末
高二数学试题
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.抛物线![]() 的准线方程为 ( )
的准线方程为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.给出四个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中能分别成为a>b的充分条件的个数为
( )
,其中能分别成为a>b的充分条件的个数为
( )
A.0 B.1 C.2 D.3
3.圆![]() 关于直线
关于直线![]() 对称,则ab的最大值为 ( )
对称,则ab的最大值为 ( )
 A.1 B.
A.1 B.![]() C.
C.![]() D.不存在
D.不存在
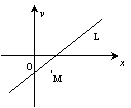
4.如图,已知点M(m,n)在直线l:Ax+By+C=0(AB≠0)的右下方,则Am+Bn+C的值 ( )
A.与A同号,与B同号 B.与A同号,与B异号
C.与A异号,与B异号 D.与A异号,与B同号
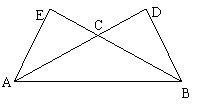 5.如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为
( )
5.如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为
( )
A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
6.直线x-y-1=0与实轴在y轴上的双曲线![]() 的交点在以原点为中心,边长为2且各边分别平行于坐标轴的正方形内部,则m的取值范围为
( )
的交点在以原点为中心,边长为2且各边分别平行于坐标轴的正方形内部,则m的取值范围为
( )
A.0<m<1 B.m<0 C.-1<m<0 D.m<-1
7.直线![]() 的倾斜角的范围是
( )
的倾斜角的范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知点A(1,2),过点(5,-2)且斜率为k的直线与抛物线y2=4x交于B、C两点,那么△ABC( )
A.是锐角三角形 B.是钝角三角形 C.是直角三角形 D.的形状与k值有关
9.设 ![]() 是双曲线
是双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() ,△
,△![]() 的面积为1,则正数b的值为
( )
的面积为1,则正数b的值为
( )
A.![]() B.2
C.
B.2
C.![]() D.1
D.1
10.若不等式![]() 对一切实数
对一切实数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() ≥1 B.
≥1 B.![]() ≤1 C.
≤1 C.![]() ≥2 D.
≥2 D.![]() ≤2
≤2
11.已知A、B分别为椭圆![]() 的左、右顶点,P是椭圆上第一象限的任一点,若∠PAB=α,∠PBA=β,则必有
( )
的左、右顶点,P是椭圆上第一象限的任一点,若∠PAB=α,∠PBA=β,则必有
( )
A.2tanα+cotβ=0 B.2tanα-cotβ=0 C.tanα+2cotβ=0 D.tanα-2cotβ=0
12.已知平面上点P∈![]() ,则满足条件的点P在平面上所形成图形的面积是
( )
,则满足条件的点P在平面上所形成图形的面积是
( )
A.36π B.32π C.16π D.4π
二、填空题:本大题共4小题,每小题4分,共16分.将答案填在题中的横线上.
13.不等式![]() 的解集是
.
的解集是
.
14.圆![]() 与
与![]() 轴交于A、B两点,圆心为P,若
轴交于A、B两点,圆心为P,若![]() ,则
,则![]() 的值为
.
的值为
.
15.设![]() ,式中
,式中![]() 满足约束条件
满足约束条件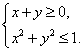 则
则![]() 的最小值是 ,最大值是 .
的最小值是 ,最大值是 .
16.已知F1、F2分别是双曲线![]() 的左、右焦点,P是双曲线上任意一点,若
的左、右焦点,P是双曲线上任意一点,若![]() 的最小值为8a,则此双曲线的离心率e的取值范围是
.
的最小值为8a,则此双曲线的离心率e的取值范围是
.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知正数a,b满足a+b=1,且n∈N*,求证:![]() .
.
18. (本小题满分12分)
已知P(2,0),Q(8,0),点M到点P的距离是它到点Q的距离的![]() ,求点M的轨迹方程,并求轨迹上的点到直线l:2x-y-5=0的最小距离.
,求点M的轨迹方程,并求轨迹上的点到直线l:2x-y-5=0的最小距离.
 19.(本小题满分12分)
19.(本小题满分12分)
已知过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于A、B两点,若以
交于A、B两点,若以![]() 为圆心的圆恰好过A、B点,求直线
为圆心的圆恰好过A、B点,求直线![]() 的方程.
的方程.
20.(本小题满分12分)
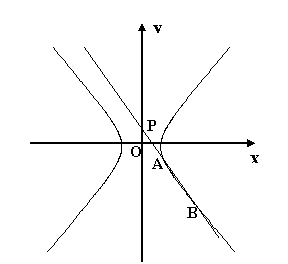 设双曲线C:
设双曲线C:![]() 与直线l:
与直线l:![]() 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围;
(II)设直线l与y轴的交点为P,且![]() ,求
,求![]() 的值.
的值.
21.(本小题满分12分)
某电器商场拟举办家电促销活动,活动前准备从厂家分批购入每台价格为2000元的某品牌空调共3600台,每批都购入x台,且每批均付运费400元.整个活动期间所付储存该空调的全部保管费是购买一批空调所付货款的![]() .现商场有专项资金22000元准备用于支付该空调的全部运费及活动期间的全部保管费.问这笔专项资金是否够用?如果不够用,至少还需要多少资金?
.现商场有专项资金22000元准备用于支付该空调的全部运费及活动期间的全部保管费.问这笔专项资金是否够用?如果不够用,至少还需要多少资金?
22..(本小题满分14分)
有对称中心的曲线叫做有心曲线,显然圆、椭圆、双曲线都是有心曲线. 过有心曲线的中心的弦叫有心曲线的直径,(为研究方便,不妨设直径所在直线的斜率存在).
定理:过圆![]() 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值-1.
上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值-1.
(Ⅰ)写出该定理在椭圆![]() 中的推广,并加以证明;
中的推广,并加以证明;
(Ⅱ)写出该定理在双曲线中![]() 的推广;你能从上述结论得到有心圆锥曲线(包括椭圆、双曲线、圆)的一般性结论吗?请写出你的结论.
的推广;你能从上述结论得到有心圆锥曲线(包括椭圆、双曲线、圆)的一般性结论吗?请写出你的结论.
参考答案
一、选择题
1.B.抛物线标准方程为![]() ,准线方程为
,准线方程为![]() .
.
2.C.①④能分别成为a>b的充分条件.
3.C.由圆的对称性知圆心(-1,2)在直线上,∴-2a-2b+2=0,即a+b=1,故![]() .
.
4.B.结合图形信息知,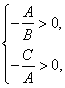 ,又原点O与点M在直线L的异侧,∴
,又原点O与点M在直线L的异侧,∴![]() ,故Am+Bn+C与B、C异号,与A同号.
,故Am+Bn+C与B、C异号,与A同号.
5.A.设AB=2c,则AE=BD=c,AD=BE=c,椭圆离心率为![]() ,双曲线离心率为
,双曲线离心率为![]() ,故离心率的倒数和为.
,故离心率的倒数和为.
6.C.由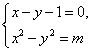 得交点坐标为(),解不等式组
得交点坐标为(),解不等式组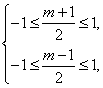 ,得-1<m<1.又双曲线焦点在y轴上,知m<0,故-1<m<0.
,得-1<m<1.又双曲线焦点在y轴上,知m<0,故-1<m<0.
7.C.设倾斜角为θ,则![]() ,故
,故![]() .
.
8.C.由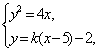 得
得![]() ,设B(x1,y1),C(x2,y2),则
,设B(x1,y1),C(x2,y2),则![]() ,记
,记![]() ,则
,则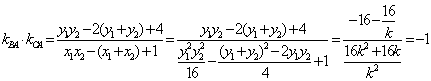 .故BA⊥CA.
.故BA⊥CA.
9.D.设PF1=m,PF2=n,则由题设知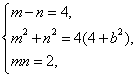 解得b=1.
解得b=1.
10.C.由![]() 恒成立知,
恒成立知,![]() ,即a≥2.
,即a≥2.
11.D.考虑极端位置,当P点落在上顶点时,有![]() ,显然有tanα-2cotβ=0成立.
,显然有tanα-2cotβ=0成立.
12.B.P点是以(2cosα,2sinα)为圆心,4为半径的圆周上的点,而当α在R上变化时,点(2cosα,2sinα)又是以(0,0)为圆心,2为半径的圆周上的点,故当圆心在半径为2的圆周上变化时,P点的轨迹形成一个内圆半径为2,外圆半径为6的圆环.故面积为36π-4π=32π.
二、填空题
13.{x―1<x<3,且x≠1}.
 14.-3.圆的标准方程为
14.-3.圆的标准方程为![]() ,在等腰直角三角形PAB中,由P到y轴的距离为2,知半径r=2,解5-c=8,得c=-3.
,在等腰直角三角形PAB中,由P到y轴的距离为2,知半径r=2,解5-c=8,得c=-3.
15.![]() ,
,![]() .如图,作出约束条件确定的可行域,在A点处有最小值,在B点处有最大值.
.如图,作出约束条件确定的可行域,在A点处有最小值,在B点处有最大值.
16.![]() .
.![]() ,当PF1=2a时取等号.因此应有c-a≤2a,即e=≤3,又e>1,故1<e≤3.
,当PF1=2a时取等号.因此应有c-a≤2a,即e=≤3,又e>1,故1<e≤3.
三、解答题
17.证明:∵a、b为正数且a+b=1,∴原不等式等价于![]() .
.
![]()
当a≥b时,a-b≥0,an≥bn,即bn-an≤0,∴(a-b)( bn-an)≤0,
当a<b时,a-b<0,an<bn,即bn-an>0,∴(a-b)( bn-an)<0,
因此![]() ≤0
≤0
即![]()
∴原不等式成立.
18. 解:设![]() ,则依条件得
,则依条件得
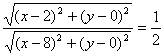
两边平方,整理得![]() ,这就是所求的轨迹方程.
,这就是所求的轨迹方程.
设圆:![]() 的圆心O到直线l:2x-y-5=0的距离为d,则
的圆心O到直线l:2x-y-5=0的距离为d,则
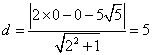
故圆上的点到直线l:2x-y-5=0的最小距离为d-4=1.
19. 解:由题设,直线![]() 的斜率必存在且不为0,设斜率为k,则
的斜率必存在且不为0,设斜率为k,则![]() 的方程为:
的方程为:![]()
由![]() 消去
消去![]() 得
得![]()
△![]()
解得![]() 且
且![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
由题意知![]() ,得
,得![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
解得![]() 或
或![]()
![]() ,
,
![]() 所求的直线方程为
所求的直线方程为![]() .
.
(注:另可利用AB的中点,及垂径分弦定理求解)
20. 解:(I)由C与![]() 相交于两个不同的点,故知方程组
相交于两个不同的点,故知方程组
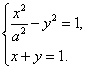
有两个不同的实数解.消去y并整理得
![]() ①
①
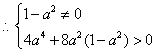
解得![]() .
.
双曲线的离心率![]() ,
,
![]() 且a≠1
且a≠1 ![]() ,
,
即离心率e的取值范围是![]() .
.
(II)设![]() ,
,
![]()
![]() 由此得
由此得![]() .
.
由于![]() 都是方程①的根,且
都是方程①的根,且![]() ,
,![]()
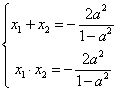
![]()
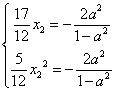
![]()
![]() ,
, ![]()
![]() (舍)或
(舍)或![]() ,
,
![]()
![]() 由
由![]() ,所以
,所以![]() .
.
21. 解:设该空调的全部运费及活动期间的全部保管费共y元,则由题意,得
![]()
![]()
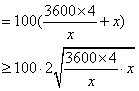
=24000.
当且仅当![]() ,即x=120时取等号.
,即x=120时取等号.
∴当x=120时,y最小,且![]() .
.
24000-22000=2000(元) ,
答:这笔专项资金不够用,至少还需要2000元资金.
22. 解:(Ⅰ)设直径的两个端点分别为A、B,由椭圆的对称性可得,A、B关于中心O(0,0)对称,所以A、B点的坐标分别为A(![]() ,B(
,B(![]() .
.
P(![]() 上椭圆
上椭圆![]() 上任意一点,显然
上任意一点,显然![]() ,
,
因为A、B、P三点都在椭圆上,所以有
![]() , ①
, ①
![]() , ②.
, ②.
而![]() ,
,
由①-②得:![]()
![]() .
.
所以该定理在椭圆中的推广为:过椭圆![]() 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值
上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值![]() .
.
(Ⅱ)该定理在双曲线中的推广为:过双曲线![]() 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值
上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值![]()
该定理在有心圆锥曲线中的推广应为:过有心圆锥曲线![]() 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值-
上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值-![]()
电话:0518-,, EMAIL:
通讯地址:江苏省东海县海陵中学 邮编:222300