江苏省南通中学2005-2006学年度第一学期期终考试复习高二数学模拟试卷 2006。1。11
班级_______学号______姓名______
一、 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1 不等式![]() 的解集是
( )
的解集是
( )
A ![]() B
B
![]() C
C
![]() D
D ![]()
2 椭圆![]() 有一点
有一点![]() ,它到左准线的距离为10,那么
,它到左准线的距离为10,那么![]() 到右焦点的距离是( )
到右焦点的距离是( )
A 8
B
3 直线![]() 过点
过点![]() ,且
,且![]() 两点到直线
两点到直线![]() 的距离相等,则
的距离相等,则![]() 的方程为 ( )
的方程为 ( )
A ![]() B
B
![]()
C ![]() 与
与![]() D
D ![]() 与
与![]()
4 下列函数中最小值是![]() 的函数是
( )
的函数是
( )
A ![]() B
B![]() C
C ![]() D
D ![]()
5 若直线![]() 的倾斜角比直线
的倾斜角比直线![]() 的倾斜角小
的倾斜角小![]() ,则直线
,则直线![]() 的斜率为
( )
的斜率为
( )
A 2
B ![]() D
D ![]()
6 当![]() ,曲线
,曲线![]() 与
与![]() 有相同的 ( )
有相同的 ( )
A 焦点 B 准线 C 焦距 D 离心率
7 设![]() 表示双曲线,则双曲线的虚轴长是 ( )
表示双曲线,则双曲线的虚轴长是 ( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
8 直线![]() 与圆
与圆![]() 的位置关系一定是 ( )
的位置关系一定是 ( )
A 相离
B 相交
C 相切
D 与![]() 的取值有关
的取值有关
9 ![]() 是“直线
是“直线![]() 与直线
与直线![]() 垂直”的 ( )
垂直”的 ( )
A 充分不必要条件 B 必要不充分条件 C 充要条件 D 不充分不必要条件
10、以椭圆两焦点为直径端点的圆交椭圆于不同的四点,顺次连接四个交点和两个焦点恰好围成一个正六边形,则这个椭圆的离心率为 ( )
A ![]() B
B
![]() C
C
![]() D
D
![]()
11 无论![]() 取何实数值,方程
取何实数值,方程![]() 所表示的曲线必不是
( )
所表示的曲线必不是
( )
A 几条直线 B 圆 C 抛物线 D 双曲线
12 ![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 到
到![]() 轴的距离为
轴的距离为![]() ,到直线
,到直线![]() 的距离为
的距离为![]() ,则
,则![]() ( )
( )
A ![]() B
B
![]() C
C
![]() D
D
![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | C | C | D | C | C | B | A | B | C | D |
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13 过点![]() ,且在两坐标轴上截距相等的直线的方程为
,且在两坐标轴上截距相等的直线的方程为![]() 。
。
14 双曲线![]() 的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为 _2__ _。
的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为 _2__ _。
15 若方程![]() 无解,则实数
无解,则实数![]() 的取值范围是
的取值范围是![]() 。
。
16 已知![]() ,则
,则![]() 的最小值是_ _16_________。
的最小值是_ _16_________。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17 解关于![]() .
.
解:![]() 原不等式
原不等式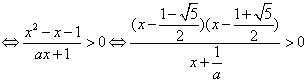 .
.
①当![]()
![]() ;
;
②当![]()
![]() ;
;
③当![]()
![]()
18 已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,弦
两点,弦![]() 的中点坐标为
的中点坐标为![]() ,
,
求:⑴直线![]() 的方程;
⑵弦长
的方程;
⑵弦长![]() 。
。
解:⑴设![]() ,则有
,则有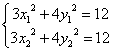
∴![]() ∴
∴![]()
∴![]() ∴
∴![]() 方程为
方程为![]() 即
即![]() 。
。
⑵由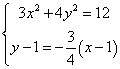 有
有![]() ∴
∴![]()
∴![]()
∴![]() ∴
∴![]()
19 设直线![]() 与抛物线
与抛物线![]() 交于相异两点
交于相异两点![]() ,以线段
,以线段![]() 为直经作圆
为直经作圆![]() (
(![]() 为圆心)。试证抛物线顶点在圆
为圆心)。试证抛物线顶点在圆![]() 的圆周上;并求
的圆周上;并求![]() 的值,使圆
的值,使圆![]() 的面积最小。
的面积最小。
|
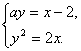
消去![]() 得:
得:![]() ,则
,则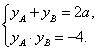
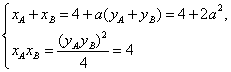
因此![]() .
.![]() ,
,
故![]() 必在圆
必在圆![]() 的圆周上。又由题意圆心
的圆周上。又由题意圆心![]() 是
是![]() 的中点,
的中点,
故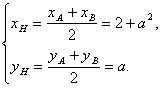 由前已证:
由前已证:
![]() 应是圆
应是圆![]() 的半径,且
的半径,且![]() 。
。
从而当![]() 时,圆
时,圆![]() 的半径最小,亦使圆
的半径最小,亦使圆![]() 的面积最小.
的面积最小.
20 双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,且
,且![]() 上动点
上动点![]() 到定点
到定点![]() 的最短距离为
的最短距离为![]() ,求双曲线
,求双曲线![]() 的方程。
的方程。
解:设双曲线![]() 的方程为
的方程为![]() ,则
,则![]() 设
设![]()
∴![]()
![]()
⑴当焦点在![]() 轴时,则有
轴时,则有![]() ,
,![]() ,
,
∴![]() ,此时双曲线
,此时双曲线![]() 的方程
的方程![]()
⑵当焦点在![]() 轴时,则有
轴时,则有![]() ,
,
①当![]() 时,
时,![]() ∴
∴![]() 不合
不合
②当![]() 时,
时,![]()
![]()
此时双曲线![]() 的方程
的方程![]()
∴所求双曲线![]() 的方程
的方程![]() 。
。
21
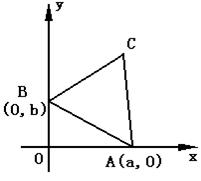
已知![]() 都是正数,
都是正数,![]() 是平面直角坐标系
是平面直角坐标系![]() 内,以两点
内,以两点![]() 和
和![]() 为顶点的正三角形,且它的第三个顶点
为顶点的正三角形,且它的第三个顶点![]() 在第一象限内。
在第一象限内。
⑴若![]() 能含于正方形
能含于正方形![]() 内, 试求:变量
内, 试求:变量![]() 的约束条件,并在直角坐标系
的约束条件,并在直角坐标系![]() 内画出约束条件表示的平面区域;
内画出约束条件表示的平面区域;
 ⑵当
⑵当![]() 在⑴所得的约束条件内移动时,求
在⑴所得的约束条件内移动时,求![]() 面积
面积![]() 的最大值,并求此时
的最大值,并求此时![]() 的坐标。
的坐标。
解: ⑴顶点![]() 是以
是以![]() 为圆心
为圆心![]() 为半径的两圆在第一象限的交点,
为半径的两圆在第一象限的交点,
由圆![]() , 圆
, 圆![]() 。
。
解得![]() ,
,![]() ,∴
,∴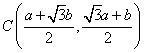
![]() 含于正方形
含于正方形![]() 内,即三顶点
内,即三顶点![]() 含于区域
含于区域![]() 内时,
内时,
 ∴
∴
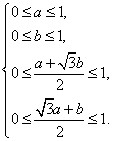
这就是![]() 的约束条件。
的约束条件。
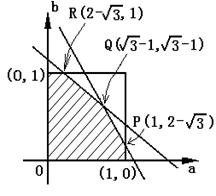
其图形为右图的六边形,∵![]() , ∴图中坐标轴上的点除外。
, ∴图中坐标轴上的点除外。
⑵∵![]() 是边长为
是边长为![]() 的正三角形,∴
的正三角形,∴![]()
在⑴的条件下, 当![]() 取最大值等价于六边形图形中的点
取最大值等价于六边形图形中的点![]() 到原点的距离最大,
到原点的距离最大,
由六边形中![]() 相应的
相应的![]() 的计算:
的计算:
![]() 、
、![]() 知:
知:
当![]() 的坐标为
的坐标为 ![]() 或
或![]() 或
或![]() 时,
时, ![]() 。
。
22
已知动点![]() 与双曲线
与双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 的距离之和为定值,
的距离之和为定值,
且![]() 的最小值为
的最小值为![]() ,⑴求动点
,⑴求动点![]() 的轨迹方程;⑵若已知
的轨迹方程;⑵若已知![]() ,
,![]() 、
、![]() 在动点
在动点![]() 的轨迹上且
的轨迹上且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:⑴由题意![]() .设
.设![]() (
(![]() ),
),
由余弦定理得:![]() .
.
又![]() ·
·![]() ,
,
当且仅当![]() 时,
时,![]() ·
·![]() 取最大值,
取最大值,
此时![]() 取最小值
取最小值![]() ,令
,令![]() ,
,
解得![]() ,
,![]() ,∴
,∴![]() ,故所求
,故所求![]() 的轨迹方程为
的轨迹方程为![]() .
.
⑵设![]() ,
,![]() ,则由
,则由![]() ,可得
,可得![]() ,
,
故![]() . ∵
. ∵![]() 、
、![]() 在动点
在动点![]() 的轨迹上,
的轨迹上,
![]()
![]() 且
且![]() ,消去
,消去![]() 可得
可得
![]() ,解得
,解得![]() ,又
,又![]() ,∴
,∴![]() ,
,
解得![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() 。
。