江苏省三星级高中海门市麒麟中学
高二数学期末复习综合测试
命题人:马林勇 姓名
一、 选择题:
1、已知点M(a,b)(ab≠0)是图![]() 内一点,直线g是以M为中点的弦所
内一点,直线g是以M为中点的弦所
在直线,直线l的方程为![]() ,则( )
,则( )
A.![]() ,且与圆相离 B.
,且与圆相离 B.![]() ,且与圆相切
,且与圆相切
C.![]() ,且与圆相交 D.
,且与圆相交 D.![]() ,且与圆相离
,且与圆相离
2、一个圆的圆心为椭圆的右焦点,且该圆过椭圆的中心交椭圆于点P, 直线PF![]() (F
(F![]() 为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、某次智力测验有6道基础知识题和4道能力提高题。每个抽答4题,基础知识题答对1题给1分,能力题答对1题给2分。要使所选题的总分值不低于7分,所选的答题方式有( )
(A)15种 (B)25种 (C)210种 (D)80种
4、在以F1(-4,0),F2(4,0)为焦点且与直线![]() 有公共点的椭圆中,短轴长最短的椭圆方程是 (
)
有公共点的椭圆中,短轴长最短的椭圆方程是 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、任意写一个无重复数字的三位数,其中十位上的数字最小的概率是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6、过椭圆![]() 的一个焦点F作弦AB,若
的一个焦点F作弦AB,若![]() ,
,![]() ,则
,则![]() 的数值为( )
的数值为( )
A.![]() B.
B.![]() C.
C.![]() D.与a、b斜率有关
D.与a、b斜率有关
7、将单词seaside的7个字母分别写在7张卡片上,从中任取4张卡片,使得4张卡片上的字母能构成单词side的概率为( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
8、已知F1、F2是两个定点,点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点,并且PF1⊥PF2,e1和e2分别是椭圆和双曲线的离心率,则有 ( )
A![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、从装有白球3个、红球4个的箱子中,把球一个一个地取出来,到第五个恰好把白球全部取出的概率是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10、对于抛物线 y2 =4x上任意一点Q,点P ( a, 0 )都满足 PQ ≥ a ,则a的取值范围是
A. (-∞,0) B. (-∞,2 ] C. [ 0,2 ] D. (0,2)
11、摇奖器摇出的一组中奖号码为8,2,5,3,7,1.从0,1,2,……,9这十个数字中任意选出六个不同的数字组成一组。如果选出的六个数字中至少有五个与摇奖器摇出的号码相同(不计顺序)就可以得奖。则中奖的概率为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12、双曲线的中心在原点,并且满足条件:⑴ 一个焦点为![]() ;⑵ 实轴长为8.则可求得双曲线的方程为
;⑵ 实轴长为8.则可求得双曲线的方程为![]() . 下列条件中:① 虚轴长为6;② 离心率为
. 下列条件中:① 虚轴长为6;② 离心率为![]() ;③ 一条准线为
;③ 一条准线为![]() ;④ 过点
;④ 过点![]() . 能够代替条件⑵的有( )
. 能够代替条件⑵的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:
13、已知直线![]() 相交于点P,直线l3过点P,当
相交于点P,直线l3过点P,当![]() 的角等于
的角等于![]() 的角时,直线
的角时,直线![]() 的方程为 。
的方程为 。
14、点P是椭圆![]() 上任一点,
上任一点,![]() 、
、![]() 是焦点,则
是焦点,则![]() 的
的
最小值与最大值之和为 .
15、设![]() 、
、![]() 是双曲线
是双曲线![]() 的两焦点,Q是双曲线上任意一点,从
的两焦点,Q是双曲线上任意一点,从![]() 引
引![]() 平分线的垂线,垂足为P,则点P的轨迹方程是
。
平分线的垂线,垂足为P,则点P的轨迹方程是
。
16、已知平面上有两定点A,B,同一平面上一动点P与两定点的连线的斜率乘积等于常数m (![]() ),对于下面5种曲线:①
直线;② 圆;③ 抛物线;④ 双曲线;⑤ 椭圆.则动点P的轨迹是____________________(将所有可能的情况都写出来)
),对于下面5种曲线:①
直线;② 圆;③ 抛物线;④ 双曲线;⑤ 椭圆.则动点P的轨迹是____________________(将所有可能的情况都写出来)
三、解答题:
17、对于二项式(1-x)10
(1)展开式的中间项是第几项?写出这一项;
(2)求展开式中各二项式系数之和
(3)求展开式中除常数项外,其余各项的系数和;
(4)写出展开式中系数最大的项;
(5)当x=2002时,求(1-x)10被2除所得的余数.
18、有三个信号监测中心A、B、C,A位于B的正东方向,
相距![]() ,相距
,相距
19、某单位组织4个部门的职工旅游,规定每个部门只能在韶山、衡山、张家界3个景区中任选一个,假设各部门选择每个景区是等可能的.
(Ⅰ)求3个景区都有部门选择的概率;
(Ⅱ)求恰有2个景区有部门选择的概率.
20、已知椭圆的中心是坐标原点O,焦点在![]() 轴上.
轴上.
(1)若椭圆的离心率为![]() ,且椭圆上的点到其准线的最短距离为
,且椭圆上的点到其准线的最短距离为![]() ,求此椭圆的方程;
,求此椭圆的方程;
(2)若过左焦点![]() 的直线
的直线![]() 交椭圆于A、B两点,且
交椭圆于A、B两点,且 ![]() .
.
(I)在(1)的条件下,求直线![]() 的方程;
的方程;
(II)求椭圆离心率e的取值范围.
高二数学期末复习综合测试(二)答案
1-6:ADBAAB 7-12 DDCAD
13、![]()
14、41
15、![]()
16、①②④⑤
17、(1)T6=-252x5
(2)210=1024
(3)a0=
(4)T5=210x4 T7=210x6
(5)(1-x)10=
18、解:取A、B所在直线为x轴,线段AB的中点O为原点,
建立直角坐标系. 则A、B、C的坐标为
A( 3, 0 )、B (-3,
0 )、C (-5,
2![]() ), (长度单位为千米)。………………4分
), (长度单位为千米)。………………4分
由已知 PB - PA = 4, 所以点P在以A、B为焦点,
实轴长为4的双曲线的右支上,…………………………………………6分
其方程为![]() (x≥2)
①…………………8分
(x≥2)
①…………………8分
又B、C同时测得同一信号,即有 PB = PC
∴ 点P又在线段BC的中垂线上, ………………………………………10分
其方程为![]() 即
即 ![]() ②…………………12分
②…………………12分
由①、② 可得点P的坐标为
( 8, 5![]() ). ………………………………14分
). ………………………………14分
19、解:某单位的4个部门选择3个景区可能出现的结果数为34.由于是任意选择,这些结果出现的可能性都相等.
(I)3个景区都有部门选择可能出现的结果数为![]() (从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有
(从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有![]() 种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为
种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为
P(A1)=![]()
(II)解法一:分别记“恰有2个景区有部门选择”和“4个部门都选择同一个景区”为事件A2和A3,则事件A3的概率为P(A3)=![]() ,事件A2的概率为
,事件A2的概率为
P(A2)=1-P(A1)-P(A3)=![]()
解法二:恰有2个景区有部门选择可能的结果为![]() (先从3个景区任意选定2个,共有
(先从3个景区任意选定2个,共有![]() 种选法,再让4个部门来选择这2个景区,分两种情况:第一种情况,从4个部门中任取1个作为1组,另外3个部门作为1组,共2组,每组选择2个不同的景区,共有
种选法,再让4个部门来选择这2个景区,分两种情况:第一种情况,从4个部门中任取1个作为1组,另外3个部门作为1组,共2组,每组选择2个不同的景区,共有![]() 种不同选法.第二种情况,从4个部门中任选2个部门到1个景区,另外2个部门在另1个景区,共有
种不同选法.第二种情况,从4个部门中任选2个部门到1个景区,另外2个部门在另1个景区,共有![]() 种不同选法).所以P(A2)=
种不同选法).所以P(A2)=![]()
20、解:(1)设椭圆的方程为![]() ,则有
,则有
![]()
![]()
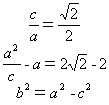 ,解得
,解得 ![]() ,
,
![]() 所求椭圆方程为
所求椭圆方程为![]() ……………………………………3分
……………………………………3分
(2)(I)由(1)知左焦点![]() 为(-1,0)
为(-1,0)
设![]() ,则由
,则由![]() ,得
,得![]()
![]() , …………………………………4分
, …………………………………4分
当![]() 轴时,则
轴时,则![]() 为x= -
为x= - ![]() ,代入
,代入![]() ,得
,得![]()
![]() ,此时不符合题意。 ………………………5分
,此时不符合题意。 ………………………5分
当![]() 不垂直
不垂直![]() 轴时,设
轴时,设![]() :
:![]() (易知
(易知![]() )
)
![]() 由
由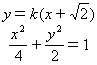 ,得
,得![]() --①…………6分
--①…………6分
![]()
又![]()
![]() ……………………………7分
……………………………7分
即![]() ,所以
,所以![]()
代入①中的![]() ,易知
,易知![]() ,
,![]()
![]() 适合
适合
![]() 综上所求直线
综上所求直线![]() 方程为
方程为
![]() 即
即![]() 或
或![]() ………………………………8分
………………………………8分
(II)设椭圆的方程为![]() ,则
,则
当![]() 轴时,
轴时,![]()
![]()
则由![]() ,得
,得![]() 即
即![]() .
.
![]() (
(![]() 舍去).--------------------------9分
舍去).--------------------------9分