江苏省苏州市吴中区2005—2006学年
高二期末考试数学试卷
一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题意要求的。
1、从10种不同的作物种子中选出6种分别放入6个不同的瓶子中展出，如果甲、乙两种种子都不许放入第一号瓶子内，那么不同的放法共有 （ ）
（A） 
种
（B） 
种
（C） 
种
（D）以上都不对
2、用1，3，5，7，9五个数字中的三个替换直线方程Ax+By+C＝0中的A、B、C，若A、B、C的值互不相同，则不同的直线共有（ ）
（A）25条 （B）60条 （C）80条 （D）181条
3、某班级英语兴趣小组有5名男生和5名女生，现要从中选4名学生参加英语演讲比赛，要求男生、女生都有，则不同的选法有 （ ）
（A）210种 （B）200种 （C）120种 （D）100种
4、
…
的值等于（ ）
(A) 
(B) 
(C) 
(D) 
5、抛物线
到直线
距离最近的点的坐标是（ ）
（A）
（B）
（C）
（D）
6、.动圆的圆心在抛物线
上，且动圆恒与直线
相切，则动圆必经过定点（）
（A）
（B）
（C）
（D）
7、设
为椭圆
左、右焦点，过椭圆中心任作一条直线与椭圆交于
两点，当四边形
面积最大时，
的值等于（ ）
（A）0 （B）1 （C）2 （D）4
8、.双曲线
两焦点为，点
在双曲线上，直线
的倾斜角之差为
，则
面积为（ ）
（A）
（B）
（C）32
（D）42
9、.已知点
，又
是曲线
上的点，则（ ）
（A）
（B）
（C）
（D）
10、.设
，集合
，若
为单元素集，则
值得个数为（ ）
（A）1 （B）2 （C）3 （D）4
11、由
展开所得x多项式中，系数为有理项的共有
A、50项 B、17项 C、16项 D、15项
12、已知椭圆
( a > b > 0) 的离心率为
，准线为
、
；双曲线
离心率为
，准线为
、
；；若、、、正好围成一个正方形，则
等于（ ）
A. 
B .
C.
D. 
二、填空题：本大题共6小题，每小题4分，共24分.
13、已知抛物线
上两点
关于直线
对称，且
，那么
的值为______________________.
14、从双曲线
上任意一点引实轴平行线交两渐近线于
两点，则
之值为______________________.
15、袋中有9个编号分别为1，2，3，…，9的小球，从中随机地取出2个，则至少有一个编号为奇数的概率是
16、相同的5个白子和相同的10个黑子排成一横行，要求每个白子的右邻必须是黑子，则不同的排法种数为 ．
17、4个人住进3个不同的房间，其中每个房间都不能空闲，则这4个人不同的住法种数是 ___________种．
18、已知A、B是互相独立事件，C与A，B分别是互斥事件，已知P(A)=0.2，P(B)=0.6，P(C)=0.14，则A、B、C至少有一个发生的概率P(A+B+C)=____________。
三、解答题：本大题共5小题，共66分.解答应写出文字说明、证明过程或演算步骤.
19、已知A={x1<log2x<3，x∈N}，B={xx-6<3，x∈N}
（1）从集A及B中各取一个元素作直角坐标系中点的坐标，共可得到多少个不同的点？
（2）从A∪B中取出三个不同元素组成三位数，从左到右的数字要逐渐增大，这样的三位数共有多少个？
（3）从集A中取一个元素，从B中取三个元素，可以组成多少个无重复数字且比4000大的自然数。
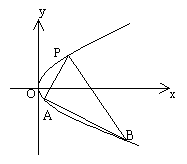
20、.如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），A（
），B（
）
均在抛物线上。
（1）写出该抛物线的方程及其准线方程
（2）当PA与PB的斜率存在且倾斜角互补时，求
的值及直线AB的斜率
21、某厂生产的A产品按每盒10件进行包装，每盒产品均需检验合格后方可出厂．质检办法规定：从每盒10件A产品中任抽4件进行检验，若次品数不超过1件，就认为该盒产品合格；否则，就认为该盒产品不合格．已知某盒A产品中有2件次品．
（1）求该盒产品被检验合格的概率；
（2）若对该盒产品分别进行两次检验，求两次检验得出的结果不一致的概率．
22、一个布袋里有3个红球，2个白球，抽取3次，每次任意抽取2个，并待放回后再抽下一次，求：
（1）每次取出的2个球都是1个白球和1个红球的概率；
（2）有2次每次取出的2个球是1个白球和1个红球，还有1次取出的2个球同色的概率；
（3）有2次每次取出的2个球是1个白球和1个红球，还有1次取出的2个球是红球的概率。
23、已知椭圆C1的方程为
，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点。
（1）求双曲线C2的方程；
（2）若直线l：
与椭圆C1及双曲线C2恒有两个不同的交点，且l与C2的两个交点A和B满足
(其中O为原点)，求k的取值范围。
高二期末考试数学试卷答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | D | B | B | C | A | C | D | B | A |
二、填空题
13、
14、a2
15、
16、
17、
18、0。82
三、解答题：
19、A={3，4，5，6，7}，B={4，5，6，7，8} ……2分
（1）A62+4=34（个）
或者当横坐标x=3时，y=4,5,6,7,8 5个
当x=4/5/6/7时，y=3,4,5,6,7,8 有4×6=24个
当x=8时 y=3,4.5.6.7 5个
因此共有点34个 ……5分
（2）C63=20（个） ……8分
（3）A中取3有
种
A中不取3，有
4种
∴
共有 + =564（种） ……12分
20. 解：（1）由已知条件，可设抛物线的方程为
点P（1，2）在抛物线上
，得
故所求抛物线的方程是
准线方程是
……4分
（2）设直线PA的斜率为
，直线PB的斜率为
则
，
PA与PB的斜率存在且倾斜角互补
……6分
由A（），B（）在抛物线上，得
（1）
（2）
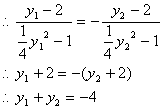
由（1）-（2）得直线AB的斜率
……12分
21、解：从该盒10件产品中任抽4件，
有等可能的结果数为
种，………………
……1分
（1）其中次品数不超过1件有
种
……2分
被检验认为是合格的概率为
……4分
（本步正确，对上两步不作要求）
．
……6分
(2)两次检验是相互独立的，可视为独立重复试验， ……7分
因两次检验得出该盒产品合格的概率均为
，故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为
…
……10分
．………………… …12分
答：该盒产品被检验认为是合格的概率为；两次检验得出的结果不一致的概率为
。
22、解：记事件A为“一次取出的2个球是1个白球和1个红球”，事件B为“一次取出的2个球都是白球”，事件C为“一次取出的2个球都是红球”，A、B、C互相独立
（1）∵
∴ 
……4分
（2）∵ 
∴ 可以使用n次独立重复试验
∴ 所求概率为
……8分
（3）本题事件可以表示为A·A·C+A·C·A+C·A·A
∴ P(A·A·C+A·C·A+C·A·A)=C31P(A)P(A)P(C)=0.324 ……14分
23、解：（1）设双曲线C2的方程为
，则
故C2的方程为
……4分
（2）将
由直线l与椭圆C1恒有两个不同的交点得
即 
①……6分
.
由直线l与双曲线C2恒有两个不同的交点A，B得
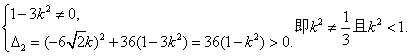……8分
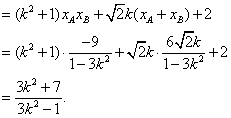
……10分
解此不等式得
③
由①、②、③得
故k的取值范围为
……14分