双曲线解答题5

80、设双曲线(>0,>0)上一点M(x₀,y₀),左、右焦点为F₁、F₂,离心率为e,记,求证该双曲线的焦半径公式是：r₁=翰林汇

81、求证：以双曲线焦半径为直径的圆,必与以双曲线实轴为直径的圆相切.翰林汇

82、求证：等轴双曲线上任一点到中心的距离是这点到两个焦点的距离的比例中项.翰林汇

83、已知双曲线的焦点为F₁、F₂(),实轴长为2a,试证明：平面内到两焦点F₁、F₂的距离的平方差的绝对值等于(2a)²的点的轨迹是已知双曲线的两条准线.翰林汇

84、等轴双曲线的顶点A,平行于实轴的弦MN,求证：△AMN是直角三角形.翰林汇

85、求证：双曲线上任一点到两条渐近线的距离的积等于定值.翰林汇

86、经过双曲线的右焦点F的直线与一条渐近线₁垂直于A，交另一条渐近线₂于B，求证：线段AB被双曲线的左准线平分。翰林汇

87、已知双曲线C：,F₁、F₂分别是它的左右焦点,抛物线l的焦点与C的右焦点重合,l的准线与C的左准线重合,P是C和l的一个交点.

求证：=1.翰林汇

88、点P在双曲线=1上,F₁、F₂为焦点,△PF₁F₂的内切圆切x轴于A点,如图,求证：A为双曲线的顶点.翰林汇

89、已知AB是双曲线过焦点F₁的任意一条弦, 以AB为直径的圆被F₁相应的准线截得圆弧MN, 求证：弧MN的度数为定值.翰林汇

90、求证：经过双曲线上任一点,作两条直线分别平行于两条渐近线,则围成的平行四边形的面积为定值.翰林汇

91、△F₁MF₂的顶点F₁、F₂是双曲线b²x²-a²y²=a²b²的两个焦点,点M在双曲线上,若∠F₁MF₂=,求证：△F₁MF₂的面积S=b²ctg.翰林汇

92、AB是双曲线的一条弦,AB的中点为M,双曲线中心为O,如果AB、OM的斜率分别为k、k₀,求证：kk₀=.翰林汇

93、设一直线交双曲线于点A、B,交双曲线的渐近线于点C、D,求证：

翰林汇94、已知点A是双曲线上的动点,O是双曲线中心,线段OA的中点为M.试求点M的轨迹方程,并证明点M的轨迹是与已知双曲线离心率相等的双曲线.翰林汇

95、证明：两条准线把两焦点间的线段分成1：2：1的双曲线是等轴双曲线.

翰林汇96、设双曲线的实轴长、虚轴长、焦距、离心率分别为2a、2b、2c、e;焦点到相应准线的距离叫焦准距,记为p;过焦点垂直于实轴的弦叫通径,其长度记为d.求证：(1)p=翰林汇

97、设双曲线的焦点在渐近线上的射影为G,求证：G是准线与渐近线的交点.

翰林汇98、已知直线l和双曲线(a＞0,b＞0)及其渐近线依次交于A,B,C,D四点(如图), 求证： AB=CD.

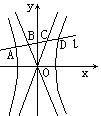　　　　　　　　　　　　 翰林汇

99、证明：双曲线的一条渐近线和一条准线交于H点,则由双曲线中心O到H的线段长等于双曲线的实半轴长.

翰林汇100、双曲线( b＞a＞0)上有两点A、B,它们与中心O的连线互相垂直,求证是定值.翰林汇

101、双曲线=1中一条准线和一渐近线的交点为M，与这条准线相对应的焦点为F，求证：MF与这条渐近线垂直。

翰林汇

102、设A、B是等轴双曲线x²－y²=a²的两个顶点，MN是该双曲线垂直于x轴的弦，如图所示，求证：∠MAN＋∠MBN=180⁰.

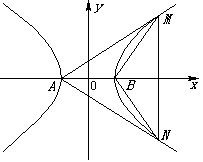　　　　　　  翰林汇

103、设F₁、F₂为双曲线(a＞0，b＞0)的左焦点和右焦点，P是其右支上的一点（非顶点），设∠PF₁F₂=α，∠PF₂F₁=β，e为双曲线的离心率，

求证：.翰林汇

104、求证：双曲线的渐近线、过焦点与该渐近线垂直的直线以及对应此焦点的准线经过同一点。

105、过点P(－2,2)的直线被双曲线x²－2y²=8截得的弦MN的中点恰好为P, 求MN的值.翰林汇

106、已知双曲线以两坐标为对称轴, 点M(3.2,2.4)是其准线和渐近线的交点, 求此双曲线的方程.

翰林汇107、一个圆的圆心在双曲线的右焦点F₂上,该圆过双曲线的中心,交双曲线于点P,直线PF₁(F₁是双曲线的左焦点)是该圆的切线,求双曲线的离心率e.

108、已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为。

　  (1) 求双曲线C的方程；

(2) 若直线l：与双曲线C恒有两个不同的交点A和B，

且(其中O为原点)，求k的取值范围。

翰林汇

双曲线解答题5 〈解答与提示〉

80、　提示：利用双曲线第二定义翰林汇

81、　提示：利用双曲线定义和三角形中位线定理证明两圆圆心距等于半径之和或半径之差的绝对值。翰林汇

82、 利用焦半径公式.

翰林汇83、　设F₁(－c，0)、F₂(c，0)，M(x，y)为轨迹上任意一点，则(x+c)²+y²－[(x－c)²+y²]=4a²　所以

翰林汇84、　提示：证明MA、NA的斜率乘积为-1

翰林汇85、　提示：用距离公式计算,定值为

翰林汇86、　，代入渐近线方程得.设AB中点的坐标为(x₀，y₀),则x₀=(x_A＋x_B)＝-.

左准线方程为x=-AB被左准线平分。

翰林汇87、　证明：

　　　　  　　　 

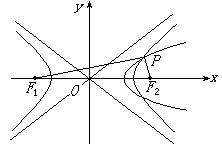
  又PF₁－PF₂=2a ∴

∴. ∴=1.

翰林汇88、　证明： 如图：PF₁=PM＋MF₁=PM＋F₁A ① PF₂=PN＋NF₂=PN＋F₂A ②

又PF₁－PF₂=2a　F₁A＋F₂A=F₁F₂=2c，PM=PN

①－②得F₁A－F₂A=F₁F₂－F₂A－F₂A=2a

∴2F₂A=2c－2a ∴F₂A=c－a

　　　　

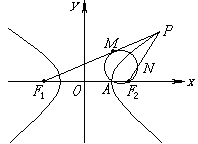
∴A(a,0)即A为双曲线一个顶点,同理可证,点P在左支上时,点A′(－a,0).

翰林汇

89、　先证圆与准线相交, 然后得弧MN的弧度数为2arccos(e为双曲线离心率).

翰林汇90、　定值为ab,a、b为双曲线的实半轴长、虚半轴长.

翰林汇91、　提示：在△F₁MF₂中使用余弦定理，并结合

翰林汇92、　提示：类比于椭圆。翰林汇

93、提示：设双曲线方程为b²x²-a²y²=a²b²,则渐近线方程为b²x²-a²y²=0,再设直线方程,利用韦达定理证明线段AB与CD的中点重合.

翰林汇94、　离心率都为.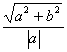

翰林汇95、　略　　　 翰林汇96、　略翰林汇　　　97、　略翰林汇

98、　证明： 若直线l不与x轴垂直, 则可设l的方程为y=kx+m, 代入双曲线方程b²x²－a²y²－a²b²=0,并整理得 (b²－a²k²)x²－2a²kmx－a²(m²+b²)=0, 设A(x₁,y₁),D(x₂,y₂), 则. 再将y=kx+m代入双曲线渐近线方程, 得b²x²－a²y²=0,并整理得(b²－a²k²)x²－2a²kmx－a²m²=0,

设B(x₃,y₃),C(x₄,y₄),则 . ∴x₁+x₂=x₃+x₄.

这说明线段AD的中点和线段BC的中点重合, 故AB=CD.翰林汇

99、　略

翰林汇100、　定值为.提示：选择中心为极点的极坐标系.翰林汇

101、　解：M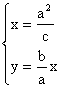：，M()，F(c，0)，

K_MF=-，∴MF与渐近线y=x垂直。

翰林汇

102、　略解.记∠MAX=α，∠MBX=β，则0＜α＜β＜90⁰.

由对称性∠MNA= 2α，∠MBN=2β，

设M(x₁，y₁)(x₁＞0，y₁＞0)，则x₁²－y₁²=a².

tgα=tg∠MAX=　tgβ=∠MBN=，

∴tgα·tgβ=·==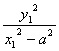1.∴tgα=tgβ=tg(90⁰－β).

∵0＜90⁰－β＜90⁰，0＜α＜90⁰.∴α=90⁰－β.

由此，可得结论，∠MAN＋∠MBN=180⁰.翰林汇

103、　提示：应用正弦定理及比例的性质.　　　翰林汇104、　略

105、　翰林汇　　　　  106、　.翰林汇

107、　解：双曲线(a＞0,b＞0),中心(0,0),c²=a²+b²,

左焦点F₁(-1,0),右焦点F₂(c,0)

圆的方程为(x-c)²+y²=c²由题意,PF₁为圆的切线,∴PF₁⊥PF₂,

∴PF₁²+PF₂²=F₁F₂².(1)又点P在双曲线上,∴PF₁-PF₂=2

又PF₂是圆的半径，∴PF₂＝c,

PF₁=2a+c,F₁F₂=2c,代入(1)式,得(2a+c)²+c²=(2c)²,

4a²+4ac-2c²=0,∴.

∴，又e＞1,∴e=.

108、解：（1）设双曲线方程为　

由已知得

故双曲线C的方程为

（2）将

由直线l与双曲线交于不同的两点得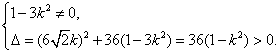

即　①　设，则

而

于是　　②

由①、②得　

故k的取值范围为

翰林汇

翰林汇