期中考复习试题

一、选择题

1.函数，已知在时取得极值，则=（　）

A.2　　　　　　　　　　　　 B.3　　　　　　　　　　　 C.4　　　　　　　　　　　D.5

2.在函数的图象上，其切线的倾斜角小于的点中，坐标为整数的点的个数（ 　）

　 A．3　　　　　　　　　　　　　 B．2　　　　　　　　　　　 C．1　　　　　　　　　　　 D．0

3.已知直线的切线则k=(　　　)

　A．　　　　　　　　　　 B．　　　　　　　　C．　　　　　　　　　D．

4.等于(　　　)

A.　　  B.　　 C. 　　　D.

5.观察下列数:1,3,2,6,5,15,14,x,y,z,122,…中x,y,z的值依次是(　　　)

A.42,41,123;　 B.13,39,123;　　C.24,23,123;　　 D.28,27,123.

6.一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是　 (　　)

A.12　　　 B.13　　　 C.14　　　　 D.15

7.在今年公务员录用中，某市农业局准备录用文秘人员二名，农业企业管理人员和农业法宣传人员各一名，报考农业公务员的考生有10人，则可能出现的录用情况种数是(　 )
A.5040　　　　　　　 B.2520　　　C.1260　　　D.210

8.如果复数（其中i为虚数单位，b为实数）的实部和虚部互为相反数，那么b等于

A.　　　　B.　　 　 C.－ 　　　　D.2

9.复数z满足z·+z+=3，则z对应点的轨迹是（　　）

A.椭圆　　　B.抛物线　　　C.圆　　　 D.双曲线

二、填空题

10.曲线y=x³在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为________

11.要做一个容积为的圆柱容器（有盖），当底面半径是　　　　  cm，高是　　　　　 ____________cm，才使原料最省.

12.观察下列式子：1+,1+＜,1+,…则可归纳出：___________.

13.对于平面几何中的命题“如果两个角的两边分别对应垂直,那么这两个角相等或互补”,在立体几何中,类比上述命题,可以得到命题“　　　　　　　　　　　　　　　　　　 ”,这个类比命题的真假性是　　　　　 .

14.设f(n)=（1+,用数学归纳法证明f(n)≥3.在“假设n=k时成立”后，f(k+1)与f(k)的关系是f(k+1)=f(k)·___________.

15.凸n边形内角和为f(k)，则凸k+1边形的内角和f(k+1)=f(k)+___________.

三、解答题

16.已知

17.求曲线围成的面积。

18.已知函数的切线方程为y=3x+1，且函数处有极值.

　 （Ⅰ）求的表达式；（Ⅱ）求函数在[－3，1]上的最大值.

19.已知函数.

⑴若函数在上单调递减，在上单调递增，求实数的值；

⑵求证：当时，在上单调递减.

20.观察以下各等式：

，分析上述各式的共同特点，猜想出反映一般规律的等式，并对等式的正确性作出证明。

　　

21.n²（n³4）个正数排成n行n列

　　　a₁₁a₁₂a₁₃……a_1n

 a₂₁a₂₂a₂₃……a_2n

 a₃₁a₃₂a₃₃……a_3n

  ………………

　　　a_n1a_n2　a_n3……a_nn

其中每一行的数成等差数列，每一列数成等比数列，并且所有公比相等。已知a₂₄=1,a₄₂=,a₄₃=.　　求a₁₁+a₂₂+a₃₃+……+a_nn

22.若函数的单调递减区间是[-1，2].

（1）求；　　

（2）求上的最大值.

参考答案

1.B  2.D  3. A  4. A　5.A　6.C  7.B　 8.C　9.C

10. _8/3_　11.2,4　 12. 1+　13.如果两个二面角的两个半平面分别对应垂直，则这两个二面角相等或互补。假命题。 14. 1+　

15. 180° 16.略　 17.略　

18. 解：（1）由

过的切线方程为：

而过

① ②

故　　 

∵　③

由①②③得　a=2，b=－4，c=5.　　

∴　

（2）

当

　

又在[－3，1]上最大值是13.

19.解：⑴　　　　　　　

∵在上单调递减，在上单调递增，

　　　　　 

⑵要使在上单调递减，则对总有

∵，∴当时，即，在

　上的最大值为或　　　　

 ∵当时，=10-4≤10，　　　　　　

∴对总有

∴当时，在上单调递减　

20.猜想：。　

证明：

　 21略

22.解： ① 因为　　　　　　　　　

根据题意的解集为　

所以，是方程的根，

由根与系数的关系，得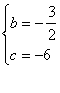　　　　　　　　　　　

②　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　

由　　　　　　　　　　　　

所以在上的最大值，是中的最大者　……10分

 　 　　

所以在上的最大值为17　　　　　　　　　　

②另解：　　　　　　　　　　

　　　　　　　　　　　　　　　　

由　　　　　　　　　　　　

，的取值情况为：

					2		4
	*	+	0	—	0	+	*
		增		减		增

　　所以在上的最大值为17