2005年全国高中数学联赛试题（二）及参考答案

一、（本题满分50分）

　　　 如图，在△ABC中，设AB>AC，过A作△ABC的外接圆的切线l，又以A为圆心，AC为半径作圆分别交线段AB于D；交直线l于E、F。

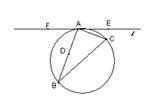
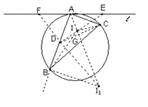
　　　 证明：直线DE、DF分别通过△ABC的内心与一个旁心。

　　　 （注：与三角形的一边及另两边的延长线均相切的圆称为三角形的旁切圆，旁切圆的圆心称为旁心。）

　　　 证明：（1）先证DE过△ABC的内心。

　　　 如图，连DE、DC，作∠BAC的平分线分别交DC于G、DE于I，连IC，则由AD=AC，

　　　 得，AG⊥DC，ID=IC.

　　　 又D、C、E在⊙A上，

　　　 ∴∠IAC=∠DAC=∠IEC，∴A、I、C、E四点共圆，

　　　 ∴∠CIE=∠CAE=∠ABC，而∠CIE=2∠ICD，

　　　 ∴∠ICD=∠ABC.

　　　 ∴∠AIC=∠IGC+∠ICG=90°+∠ABC，∴∠ACI=∠ACB，∴I为△ABC的内心。

　 （2）再证DF过△ABC的一个旁心.

　　　 连FD并延长交∠ABC的外角平分线于I₁，连II₁、B I₁、B I，由（1）知，I为内心，

　　　 ∴∠IBI₁=90°=∠EDI₁，∴D、B、l₁、I四点共圆，

　　　 ∵∠BI l₁ =∠BDI₁=90°－∠ADI₁

　　　 =（∠BAC+∠ADG）－∠ADI=∠BAC+∠IDG，∴A、I、I₁共线.

　　　 I₁是△ABC的BC边外的旁心

二、（本题满分50分）

　　　 设正数a、b、c、x、y、z满足

　　　 求函数的最小值.

解：由条件得，，

　　　 即，

　　　 ，同理，得

a、b、c、x、y、z为正数，据以上三式知，　　 ，

　　　 故以a、b、c为边长，可构成一个锐角三角形ABC，

　　　  ，问题转化为：在锐角△ABC中，

　　　 求函数、、）=的最小值.

　　　 令则

　　　 且

　　　

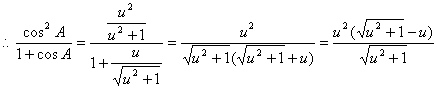
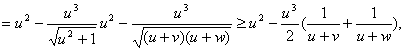
　　　 同理，

　　　

+（取等号当且仅当，此时，

三、（本题满分50分）

　　　 对每个正整数n，定义函数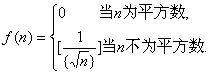

　　　 （其中[x]表示不超过x的最大整数， 试求：的值.

解：对任意，若，则，设

　　　 则

　　　 让a跑遍区间）中的所有整数，则

　　　 于是……①

　　　 下面计算画一张2k×2k的表，第i行中，凡是i行中的位数处填写“*”号，则这行的“*”号共个，全表的“*”号共个；另一方面，按列收集“*”号数，第j列中，若j有T（j）个正因数，则该列使有T（j）个“*”号，故全表的“*”号个数共

个，因此=.

示例如下：

j i	1	2	3	4	5	6
1	*	*	*	*	*	*
2		*		*		*
3			*			*
4				*
5
6						*

　　　 则

……②

　　　 由此，……③

　　　 记易得的取值情况如下：

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	3	5	6	6	7	8	6	9	8	8	8	10	7	10	10

　　　 因此，……④

　　　 据定义，

　　　 又当，

　　　 ，

　　　 ，则……⑤

　　　 从则