人大附中2005-2006学年度第一学期高二数学期末测试

一．单项选择题.

1.椭圆 上一点 到一个焦点的距离等于3，则它到另一个焦点的距离为（　　　）　　　　 A．5　　　　  B．7　　　　  C．8　　　　　  D．10

2.如果方程 表示焦点在 轴上的椭圆，那么实数 的取值范围是（　　 ）A． 　　　　  B．（0，2）　　　  C． 　　　　　 D．（0，1）

3. 椭圆 与 的关系为（　　　）

A．有相等的长、短轴　B．有相等的焦距C．有相同的焦点D．有相同的准线

4. 方程 所表示的曲线为 ．

　　①若曲线 为椭圆，则 ；②若曲线 为双曲线，则 或 ；③曲线 不可能是圆；④若曲线 表示焦点在 轴上椭圆，则

以上命题正确的是（　　　 ）　　　

A．②③　　　　  B．①④　　　　  C．②④　　　　　 D．①②④　

5. 设双曲线 的一条准线与两条渐近线交于 、 两点，相应焦点为 ，若 为正三角形，则双曲线的离心率为（　　　）

　　A． B．3　　C．  D．2　　　

6. 已知抛物线 的焦点为 ，定点 ，在此抛物线上求一点 ，使 最小，则 点坐标为（　　　）

　　A． 　B． 　C． 　 D． 

7. 动点 到点 的距离比到直线 的距离小2，则动点 的轨迹方程为（　　 ）A． 　 B． 　 C． 　 D．　

8. 已知双曲线的一条准线与抛物线的准线重合，则该双曲线的离心率为（　　　 ）

A．　B．　　 C． D．

二．填空题.　

9.如果椭圆 与双曲线 的焦点相同，那么 ．

10. 以椭圆 的焦点为顶点，顶点为焦点的双曲线方程是______．

11. 斜率为1的直线经过抛物线 的焦点，与抛物线相交于两点 、 ，则线段 的长是____．

12. 抛物线形拱桥，当水面宽 时，水面离拱顶为 ，若水下降 ，则此时水面宽为___________.

三．解答题.

13. 已知双曲线与椭圆 共焦点，它的一条渐近线方程为 ，求双曲线的方程．

　　　

14． 已知动圆 过定点 ，并且在定圆 的内部与其相内切，求动圆圆心 的轨迹方程．

　

 15. 已知椭圆 及直线 ．（1）当 为何值时，直线与椭圆有公共点？（2）若直线被椭圆截得的弦长为 ，求直线的方程．

　　

16．设两点在抛物线上，l是AB的垂直平分线.

　 （Ⅰ）当且仅当取何值时，直线l经过抛物线的焦点F？证明你的结论；

　　　 (Ⅱ)(文)当时，求直线的方程.

　 　(Ⅱ)(理)当直线l的斜率为2时，求l在y轴上截距的取值范围.

　　　

2005-2006学年度第一学期高二数学期末测试参考答案

一．单项选择题.

1.B　 2.D　　3.B　　4. C5.D　　6.C　　7.D　 8.D

二．填空题.

9.　1　

10.

11. 8

12.

三．解答题.

13.

　　　解法一：由于双曲线的一条渐近线方程为 ，则另一条为 ．可设双曲线方程为

即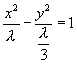

　　由椭圆方程 可知

　　双曲线与椭圆共焦点，则 　∴ ．

　　故所求双曲线方程为 ．

　　解法二：双曲线与椭圆共焦点，可设双曲线方程为

　　由渐近线方程 可得

　 ∴

　　故所求双曲线方程为

　　点评：1．渐近线为 的双曲线方程可表示为

14．

　　　　解：设动圆 和定圆 内切于点 ．动点 到两定点，即定点 和定圆圆心 距离之和恰好等于定圆半径，即 ．

　　∴点 的轨迹是以 ， 为两焦点，半长轴为4，半短轴长为 的椭圆的方程： ．

　　说明：本题是先根据椭圆的定义，判定轨迹是椭圆，然后根据椭圆的标准方程，求轨迹的方程．这是求轨迹方程的一种重要思想方法．

 15.

　　解：（1）把直线方程 代入椭圆方程 得

　　，即 ．

　　，

　　解得 ．　　

　　（2）设直线与椭圆的两个交点的横坐标为 ， ，由（1）得

， ．

　　根据弦长公式得　　

　　 ．

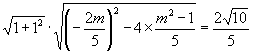　　解得 ．

　　因此，所求直线的方程为 ．

　　说明　处理有关直线与椭圆的位置关系问题及有关弦长问题，采用的方法与处理直线和圆的有所区别．这里解决直线与椭圆的交点问题，一般考虑判别式 ；解决弦长问题，一般应用弦长公式．用弦长公式，若能合理运用韦达定理（即根与系数的关系），可大大简化运算过程．

16．

　　　 解：（Ⅰ）两点到抛物线的准线的距离相等.

∵抛物线的准线是x轴的平行线，不同时为0，

∴上述条件等价于

∵，　 ∴上述条件等价于　

即当且仅当时，l经过抛物线的焦点F.

另解：（Ⅰ）∵抛物线，即，

∴焦点为………………………………………………………1分

（1）直线的斜率不存在时，显然有………………………………3分

（2）直线的斜率存在时，设为k， 截距为b

即直线：y=kx+b　　　由已知得：

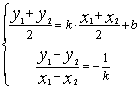……………5分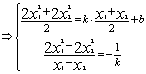　　

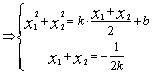……………7分　　

即的斜率存在时，不可能经过焦点……………………………………8分

所以当且仅当=0时，直线经过抛物线的焦点F…………………………9分

（Ⅱ）（文）当时，

直线的斜率显然存在，设为：y=kx+b………………………………10分

则由（Ⅰ）得：　　　　　　　　　　　　　　　　

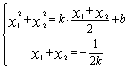
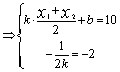　 ………………………11分

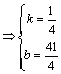…………………………………………13分

所以直线的方程为，即………………14分

（II）(理)设l在y轴上的截距为b，依题意得l的方程为；过点A、B的直线方程可写为，所以满足方程得；

　　　 A，B为抛物线上不同的两点等价于上述方程的判别式

　　　 即

　　　 设AB的中点N的坐标为，则

　　　

　　　 由

　　　 即得l在y轴上截距的取值范围为（）.