试卷类型:A
山东省滨州市2005~2006学年度第一学期期末考试
高二数学试题(理科:必修5+选修2‐1)
(人教A版) 2006年1月16日
考生注意:
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间120分钟
第I卷(选择题 共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型用2B铅笔涂写在答题卡上.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.不能答在试题卷上.
3.考试结束后,监考人员将第I卷和答题卡一并收回.
一、选择题:本题共12小题;每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
⑴ 在![]() 中,若
中,若![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
⑵ 曲线![]() 在点(
在点(![]() )处切线的倾斜角为
( )
)处切线的倾斜角为
( )
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
⑶ 已知![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,![]() 是
是![]() 的必要条件,那么
的必要条件,那么![]() 是
是![]() 成立的:
( )
成立的:
( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分,也不必要条件
⑷ 以![]() 的焦点为顶点,顶点为焦点的椭圆方程为
( )
的焦点为顶点,顶点为焦点的椭圆方程为
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
⑸ 若一个等差数列前3项的和为30,最后三项的和为150,且所有项的和为300,则这个数列有( )
(A)12项 (B)11项 (C)10项 (D)9项
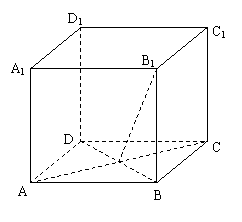 ⑹ 如图,长方体
⑹ 如图,长方体![]() 中,AC与BD的交点为M,设
中,AC与BD的交点为M,设![]() a,
a,![]() =b,
=b,![]() c,则下列向量中与
c,则下列向量中与![]() 相等的向量是:( )
相等的向量是:( )
(A)![]() a +
a + ![]() b + c
b + c
(B) ![]() a +
a + ![]() b + c
b + c
(C) ![]() a -
a -![]() b + c
b + c
(D) ![]() a -
a - ![]() b + c
b + c
⑺ ![]() ( )
( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
⑻ 曲线![]() 与直线
与直线![]() 所围成图形的面积等于
( )
所围成图形的面积等于
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
⑼ 正三棱柱(侧棱与底面垂直,底面是正三角形的棱柱)的体积是V,当其表面积最小时,底面边长是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
⑽ 在一座20m高的观测台测得地面一水塔顶仰角为![]() ,塔底俯角为
,塔底俯角为![]() ,那么这座塔的高为 ( )
,那么这座塔的高为 ( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
⑾ 若A(3,2),F为抛物线![]() 的焦点,P在抛物线上,则使
的焦点,P在抛物线上,则使![]() 最小时的P点坐标为( )
最小时的P点坐标为( )
(A)(2,2) (B)(3,![]() ) (C) (3,-
) (C) (3,-![]() ) (D) (3,±
) (D) (3,±![]() )
)
⑿ 已知三个不等式:①![]() ; ②
; ②![]() ; ③
; ③![]() ≤0.要使同时满足①式和②式的所有x的值都满足③式,则实数m的取值范围是
( )
≤0.要使同时满足①式和②式的所有x的值都满足③式,则实数m的取值范围是
( )
(A)![]() (B)
(B) ![]() (C)
(C)![]() ≤6 (D)0<
≤6 (D)0<![]() ≤9
≤9
第II卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
⒀在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
⒁若正数![]() 满足
满足![]() ,则
,则![]() 的取值范围是 .
的取值范围是 .
⒂到定点(3,0)的距离和到直线![]() 的距离的比是常数
的距离的比是常数![]() 的点的轨迹方程是 .
的点的轨迹方程是 .
⒃下列命题中:
①若![]() 为两个命题,则“
为两个命题,则“![]() 且
且![]() 为真”是“
为真”是“![]() 或
或![]() 为真”的必要不充分条件;
为真”的必要不充分条件;
②若![]() 为:
为:![]() ≤0,则
≤0,则![]() ;
;
③若椭圆![]() 的两焦点为
的两焦点为![]() ,且弦AB过
,且弦AB过![]() 点,则
点,则![]() 的周长为16;
的周长为16;
④若![]() ;
;
所有正确命题的序号是 .
三、解答题:本大题共6小题,满分74分.解答应写出文字说明、证明过程或推演步骤.
⒄(本小题满分12分)
已知等比数列![]() 中,
中,![]() ,求其第4项及前5项和.
,求其第4项及前5项和.
⒅(本小题满分12分)
已知函数![]()
(I) 求出函数的单调区间;
(II)求![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
⒆(本小题满分12分)
已知![]() 满足条件
满足条件
求![]() 的最大值和最小值.
的最大值和最小值.
⒇(本小题满分12分)
如图,直三棱柱(侧棱垂直于底面的棱柱)![]() ,底面
,底面![]() 中
中![]() ,棱
,棱![]() ,
,![]() 分别为
分别为![]() D的中点.
D的中点.
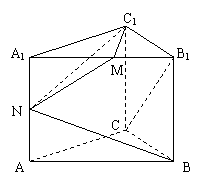 (I) 求
(I) 求![]() 的长;
的长;
(II) 求![]() >的值;
>的值;
(III)求证:![]() .
.
(21)(本小题满分12分)
某地为发展旅游产业,在原有基础上,本年度投入资金800万元进行生态环境建设,并且以后每年都有资金投入,但是均比上年减少![]() .本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进,预计今后的旅游业收入每年会比上年增加
.本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进,预计今后的旅游业收入每年会比上年增加![]() .
.
(I)设n年内(本年度为第一年)总投入为an万元,旅游业总收入为bn万元.写出 an,bn的表达式;
(II)至少经过几年旅游业的总收入才能超过总投入?
(22)(本小题满分14分)
已知中心在坐标原点的双曲线C的右焦点为(2,0),右顶点为(![]() ,0)
,0)
(I) 求双曲线C的方程;
(II) 求若直线![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且![]() (其中O为原点),求
(其中O为原点),求![]() 的取值范围;
的取值范围;
(III) 已知点![]() ,在(II)的条件下,求
,在(II)的条件下,求![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
参考答案
一、选择题(本题共12小题;每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | D | C | A | D | C | B | B | A | C |
二、填空题(本大题共4小题,每小题4分,共16分)
13.![]() 14.
14.![]() 15.
15.![]() 16.②④
16.②④
三、解答题(本大题共6小题,满分74分)
17.解:设公比为![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分
由已知得  ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 3分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 3分
|
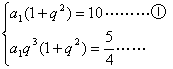 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 5分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 5分
②÷①得 ![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7分
将![]() 代入①得
代入①得 ![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
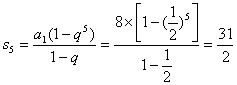 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12分
18.解:(Ⅰ)![]() ,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 1分
,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 1分
列表如下:
|
|
| -1 |
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↗ |
| ↘ |
| ↗ |
┄┄┄┄┄┄┄┄┄ 5分
由上表可知![]() 和
和![]() 均为函数的单调递增区间,
均为函数的单调递增区间,
![]() 为函数的单调递减区间 . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7分
为函数的单调递减区间 . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7分
(Ⅱ)极值点-1,![]() 均属于
均属于![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
又![]() , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
, ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
故![]() 在
在![]() 上的最小值是
上的最小值是![]() ,最大值是16. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12分
,最大值是16. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12分
19.解:在同一坐标系中,作直线![]() ,再根据不定式组确定可行域
,再根据不定式组确定可行域![]() (如图).
(如图).
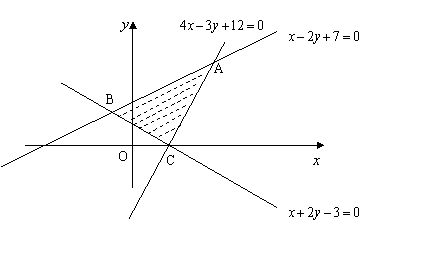
┄┄┄┄┄┄┄┄┄┄┄ 6分
把![]() 看作点
看作点![]() 到原点O的距离的平方.
到原点O的距离的平方.
由![]() 解得点A
解得点A![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
所以
![]() ; ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
; ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
因为原点到直线BC的距离为![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 11分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 11分
所以
![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12分
20.解:如图,以C为原点,CA、CB、CC1所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的坐标系
轴,建立如图所示的坐标系![]() -
-![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 1 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 1 分
(Ⅰ)依题意得![]()
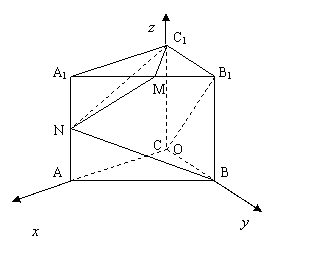
![]()
∴ 线段BN的长为 ![]() . ┄┄┄┄┄┄ 3 分
. ┄┄┄┄┄┄ 3 分
(Ⅱ)依题意得![]() ,
,
∴ ![]()
∴![]()
![]() , ┄┄┄┄ 5 分
, ┄┄┄┄ 5 分
∴![]() >=
>=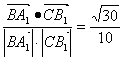 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7 分
(Ⅲ) 依题意得![]() ∴
∴ ![]() ,
,
∴ ![]() ,
,![]() ,
,![]() ,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄
9 分
,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄
9 分
∴
![]()
![]()
∴ ![]() ,
,![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 11 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 11 分
∴ ![]()
∴
![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12 分
21 解.(I)第1年投入为800万元.
第2年投入为800×(1-![]() )万元,
)万元,
第n年投入为800×(1-![]() )n-1万元. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 1 分
)n-1万元. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 1 分
所以,n年的总收入为
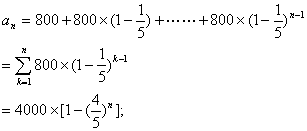 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 3 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 3 分
第 1年旅游业收入为 400万元,
第 2年旅游业收入为 400 ×(1+![]() )万元,
)万元,
第n年旅游业收人为400×(1+![]() )n-1
万元.
┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 4 分
)n-1
万元.
┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 4 分
所以,n年内的旅游业总收入为
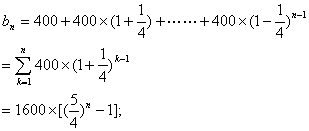 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 6 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 6 分
(II)设至少经过n年旅游业的总收入才能超过总投入,由此
![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7 分
![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8 分
![]()
![]()
 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄
10 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄
10 分
![]()
![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 11 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 11 分
∴ 至少经过5年旅游业的总收入才能超过总投入 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 12 分
22.解:(Ⅰ)设双曲线方程为![]() ,
,
由已知得 ![]()
故所求双曲线的方程为 ![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 4 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 4 分
(Ⅱ) 将![]() 代入
代入 ![]() ,可得
,可得
![]()
由直线![]() 与双曲线C恒有两个不同的交点,得
与双曲线C恒有两个不同的交点,得
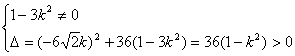
故![]() ┄┄ ①
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 6 分
┄┄ ①
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 6 分
设![]() ,则
,则
![]()
由![]() 得
得 ![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8 分
而![]()
![]()
∴
![]() 解此不定式得
解此不定式得 ![]() ┄┄ ② ┄┄┄┄┄┄┄┄┄┄┄ 9 分
┄┄ ② ┄┄┄┄┄┄┄┄┄┄┄ 9 分
由①,②得 ![]()
故 ![]() 的取值范围是
的取值范围是![]() ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10 分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10 分
(Ⅲ)点M到直线![]() 的距离为:
的距离为: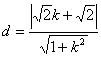
∴
![]()
![]() ┄┄┄┄┄┄┄┄┄┄┄┄ 12 分
┄┄┄┄┄┄┄┄┄┄┄┄ 12 分
设 ![]() ,
,![]()
则 ![]() , ∵
, ∵
![]() ∴
∴
![]()
∴ ![]() 在区间
在区间![]() 上均为增函数.
上均为增函数.
当![]() 时,
时,![]() ,
,
即 ![]() ,此时
,此时 ![]() ;
;
当![]() 时,
时,![]() ,
,
即 ![]() ,此时
,此时 ![]() ;
;
综上所得![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围是
的取值范围是![]()
![]() ┄┄┄┄┄┄┄ 14 分
┄┄┄┄┄┄┄ 14 分