山西大学附中2005—2006年下学期高二数学期中试题

一.　 选择题(本题共36分,每小题3分)

1.直线a//平面α, 直线b//平面α,那么直线a与b的位置关系是（　　 ）

A.平行　　　　　　 B.相交　　　　　  C.异面　　　　　 D.都有可能

2.下列说法正确的是（　　 ）

A. 正三棱锥是正四面体;　　　　　　　　　　 B. 长方体是正四棱柱;

C. 平行六面体不可能是直四棱柱　　　　　　  D. 正四棱柱是长方体.

3.已知点E是以点P为顶点的棱锥的某一条侧棱PA上的一个三等分点，PE=2EA，过点E且平行于棱锥底面的截面面积为S₁，棱锥的底面面积为S₂，则S₁:S₂= （　　 ）　　

A. 1:9　　　　　  B. 4:1　　　　　  C. 2:3　　　　　  D. 4:9

4.正四棱锥P-ABCD的斜高等于底面的边长，则相对的两个侧面PAB与PDC所成二面角的度数是（　　 ）　 A. 　　　　 B. 　　　　　C. 　　　　　 D.

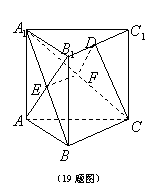
5. 在三棱锥P-ABC中,PA⊥平面ABC, ∠ABC=, 则下列结论中:

①平面PAC⊥平面ABC; ②平面PAB⊥平面PBC; ③平面PAC⊥平面PBC;

④平面PAB⊥平面PAC. 其中一定正确的有（　　 ）

A.①②　　　　　　  B.①③　　　　　　 C.①④　　　　　　  D.②③

6. 空间四点每两点的连线长都是，动点在线段上，动点在线段上，则点与点的最小距离是（　　 ）

A.　　　　 B.　　　　 C.　　　　 D.

7. 棱长为a正方体ABCD-A₁B₁C₁D₁中, 点E是棱AA₁的中点, 点F是对角线BD₁的中点, 则下列说法中不正确的是（　　 ）

A. EF是异面直线AA₁与BD₁的公垂线;　　　B. EF//平面ABCD;

C. EF与BC₁成的角;　　　　　　　　　 D. EF与BC的距离等于.

8. 二面角α—l—β的平面角为60⁰，A、B∈l，ACα，BDβ，AC⊥l，BD⊥l，若AB=AC=BD=1，则CD的长为 （　　 ）　　

A.　　 　　　　B.　　　　  C.2　　 　　　　  D.

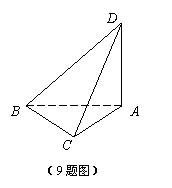
9. 把一副三角板ABC与ABD摆成右图所示的直二面角D-AB-C,则异面直线DC与AB所成角的正切值为（　　 ）　

 A. 　　　B. 　　 C. 　　 D. 不存在

10. 在棱长为1的正方体的密闭容器中，棱和棱的中点处各有一个小孔，顶点处也有一个小孔，若正方体可任意放置，且小孔面积不计，则这个正方体容器中最多可容纳水的体积是（　　 ）

A.　　　 B. 　　C.　　　　  D.

11. 平面与平面相交成一个锐二面角，平面上的一个圆在平面上的射影是一个离心率为的椭圆，则等于（　　 ）　　　　　　　　　　　　　　　　 　　　　　 

A.　　　　　　 B.　　　　  C.　　　　  D.

12. 、、三点在半径为6的球面上，且它们两两之间的球面距离为，则球心到平面的距离是（　　 ）　　　　　　　　　　　　　　　　　　　　　　　　

 A.　　　　　B.　　 　　 C.　　  　　D.

二.填空题(本题共16分,每小题4分)

13.一个球的内接正方体与外切正方体的表面积之比是　　　　　　 .

14. 已知是边长为的正三角形，那么在空间与这个三角形的三个顶点的距离都等于1的不同平面的个数有　　　　　　　　　 .

15．正四面体的外接球半径为，内切球半径为，则与之比是　　　　　　　

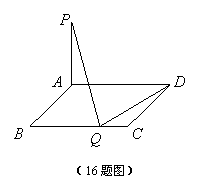
16．如图，已知矩形中，，平面，若在上有且仅有一个点满足，则的长是　　　　　　

三.解答题(本题共48分,每小题12分)

17. （本小题12分）已知直三棱柱ABC-A₁B₁C₁中，AC=BC=CC₁，∠ACB=.

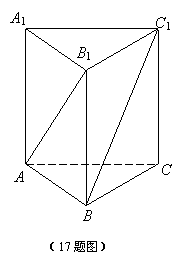(1)求证：AB₁⊥BC₁

(2)求异面直线A₁B₁与BC₁所成的角.

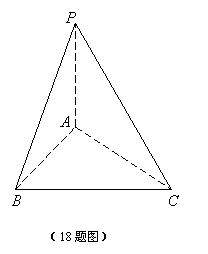
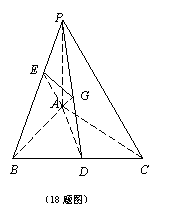
18. （本小题12分）已知三棱锥P-ABC的底面是等腰直角三角形，A为直角顶点，PA⊥底面ABC，点A在平面PBC上的射影恰好是△PBC的重心，求二面角A-PB-C的大小.

19. （本小题12分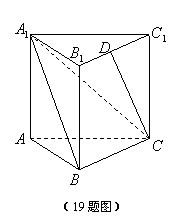）在直三棱柱中，点是的中点，底面三角形是直角三角形，，，，

　  （1）求C₁到平面A₁BC的距离;

（2）求直线与平面所成的角.

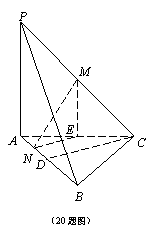
20. （本小题12分）已知三棱锥P-ABC的底面为正三角形, PA⊥平面ABC, 点M、N分别在PC、AB上，且PM=MC，BN=3NA.

(1)求证: MN⊥AB;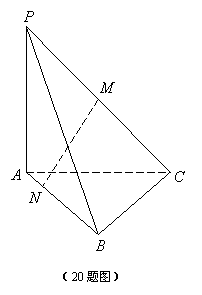　　　 (2)若BC=2, 且MN与底面ABC成角,求三棱锥P-ABC的体积.

2005---2006年山大附中下学期期中高二数学答案

一.选择题(本题共36分,每小题3分)

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	D	D	B	A	B	D	A	B	C	A	B

二.填空题(本题共16分,每小题4分)

13.　1:3　　　.　　14.　5个　　　　 .15．　　3:1　　  16．　 2　　　　 

三.解答题(本题共48分,每小题12分)

17. 解:(1)连接B₁C,

　

　

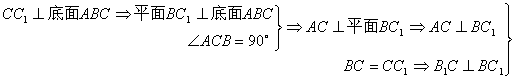
(2),

连接AC₁,在△ABC₁中,

　 由于　AC=BC=CC₁　 且　 AC、BC、CC₁两两垂直

　 所以　 AB=BC₁=AC₁所以　∠ABC₁=

　所以异面直线A₁B₁与BC₁所成的角是

18..解：取BC的中点D，连接AD、PD，

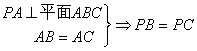　∵ 且PA⊥AD

　∴ 点G在PD上，且 DG=DP，

　连接AG，则AG⊥平面PBC，

　过G作GE⊥PB于E，连接AE，则AE⊥PB，

　∴ ∠AEG是二面角A-PB-C的平面角.

　在Rt△PAD中， AG⊥PD

　设AD=a，则　　又

　∴  ∴ ，从而　

又易得：　，　　  ∴

∴ ，∴

因此，所求二面角的大小是

19.解：（1）

所以C₁到平面A₁BC的距离等于B₁到平面A₁BC的距离

，

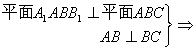
连接交于，则，　所以　EB₁⊥平面A₁BC

又 ,　∴ 所以C₁到平面A₁BC的距离等于.

（2）取的中点F，连接EF、DF，　 则　　 　　 所以，

又　EB₁⊥平面A₁BC　 所以　DF⊥平面A₁BC　∴ 即为直线与平面所成的角.

且　 ，　 ∴ ， .

所以，直线与平面所成的角为.

20. 解：（1）取AC的中点E，AB的中点D，连接ME、NE、CD，

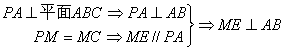
又

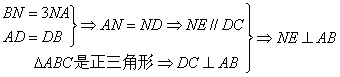
∴ AB⊥平面MNE　　　　∴ AB⊥MN

（2）由（1）可知：PA⊥平面ABC,且ME//PA　 ∴ ME⊥平面ABC

∴ ∠MNE=，　∴ ME=NE

在正△ABC中，BC=2，　　 故有　PA=2ME=2NE=DC=，

所以三棱锥P-ABC的体积