孟州五中05-06学年下学期高二年级期中考试卷
数 学
说明:本试卷分第I卷和第II卷两部分。第I卷60分,第II卷90分,共150分,答题时间120分钟。
第I卷(选择题,共60分)
一、选择题(每小题5分,共60分,请将所选答案填在答题卡上)
1、下列说法不正确的是
A,如果一条直线的两点在一个平面内,则这条直线的所有点都在这个平面内.
B,如果两个平面有一个公共点,则它们还有其他公共点,且它们都在一条直线上.
C,三点确定一个平面. D,平行于同一条直线的两条直线互相平行
2、给出下列四个命题:
(1)空间四点共面,则其中必有三点共线
(2)空间四点不共面,则其中任何三点不共线
(3)空间四点中存在三点共线,则此四点共面
(4)空间四点中任何三点不共线,则此四点不共面
其中正确的有( )
A.(2)(3) B(1)(2)(3) C(1)(2) D(2)(3)(4)
3、球的体积是π,则此球的表面积是( )
A. 12π B. 16π C. π D. π
4、若点E、F、G、H顺次为空间四边形ABCD四条边AB、BC、CD、DA的中点,EG=3,FH=4,则![]() 的值为(
)
的值为(
)
A. 25
B.
5、两条异面直线在同一个平面内的射影一定是( )
A 两条相交直线 B 两条平行直线
C 两条相交直线或两条平行直线 D 以上都不对
6、下列命题中正确的是:①底面是正多边形的棱锥是正棱锥 ②侧棱都相等的棱锥是正棱锥③侧面是等腰三角形的棱锥是正棱锥 ④侧棱都相等且底面是各边相等的圆内接多边形,这个棱锥是正棱锥
A.④ B.③④ C.②③ D.①③④
7、下列四个命题:
① 平行于同一条直线的两平面平行 ② 平行于同一个平面的两平面平行 ③ 垂直于同一条直线的两平面平行 ④ 与同一条直线成等角的两平面平行
其中正确的命题是( )
A.①② B.②③ C.③④ D.②③④
8、“![]() ∥
∥![]() ,
,![]() ∥
∥![]() ”是“∠
”是“∠![]() =∠
=∠![]() ”的( )
”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分又不必要条件
9、在空间四边形![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的中点,则
上的中点,则![]() 与
与
![]() 的大小关系为( )
的大小关系为( )
A. 相等 B.MN >![]() C.MN<
C.MN<![]() D.不能确定
D.不能确定
10、下列命题正确的是( )
A. 过平面外的一条直线只能作一平面与此平面垂直
B. 平面![]() ⊥平面
⊥平面![]() 于
于![]() ,
,![]() ,
,![]() ,则
,则![]()
C. 一直线与平面![]() 的一条斜线垂直,则必与斜线的射影垂直
的一条斜线垂直,则必与斜线的射影垂直
D. ![]() 、
、![]() 、
、![]() 是两两互相垂直的异面直线,
是两两互相垂直的异面直线,![]() 为
为![]() 、
、![]() 的公垂线,则
的公垂线,则![]() ∥
∥![]()
11、从平面外一点向平面引一条垂线和三条斜线,若这些斜线与平面成等角,则如下四个命题中:① 三斜足构成正三角形;② 垂足是斜足三角形的内心;③垂足是斜足三角形的外心; ④ 垂足是斜足三角形的垂心。其中正确命题的个数是( )。
(A)1 (B)2 (C)3 (D)4
12、若a,b,l是两两异面的直线,a与b所成的角是![]() ,l与a、l与b所成的角都是
,l与a、l与b所成的角都是![]() ,则
,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.[![]() ] B.[
] B.[![]() ] C.[
] C.[![]() ] D.[
] D.[![]() ]
]
第II卷(非选择题,共90分)
二、填空题(每小题4分,共16分,答案填在答题卡上)
13、直角三角形![]() 的斜边
的斜边![]() 在平面
在平面![]() 内,直角顶点
内,直角顶点![]() 在平面
在平面![]() 外,
外,![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,且
,且![]() ,则Δ
,则Δ![]() 为 三角形。
为 三角形。
14、OX,OY,OZ是空间交于同一点O的互相垂直的三条直线,点P到这三条直线的距离分别为3,4,7,则OP长为_______.。
15、在北纬![]() 圈上有甲乙两地,它们在纬度圈上的弧长为
圈上有甲乙两地,它们在纬度圈上的弧长为![]() (
(![]() 为地球的半径),则甲乙两地的球面距离为
。
为地球的半径),则甲乙两地的球面距离为
。
16、平行六面体![]() 中,
中,![]() =4,
=4,![]() =3,
=3,![]() =5, ∠
=5, ∠![]() =90°, ∠
=90°, ∠![]() =∠
=∠![]() =60°, 则对角线
=60°, 则对角线![]() 的长为___________ 。
的长为___________ 。
三、解答题(本大题共74分,17—21题每题12分,22题14分)
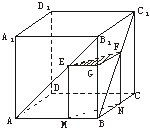
17、(本小题满分12分):正方体ABCD—A1B
18、(本小题满分12分). .已知正方形ABCD的边长为1,分别取边BC、CD的中点E、F,连结AE、EF、AF,以AE、EF、FA为折痕,折叠使点B、C、D重合于一点P.
(1)求证:AP⊥EF;
(2)求证:平面APE⊥平面APF;
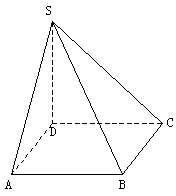
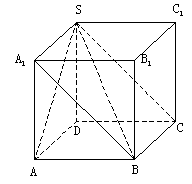
19、(本小题满分12分)如图,
四棱锥![]() 的底面是边长为1的正方形,
的底面是边长为1的正方形,
SD垂直于底面ABCD,SB=√3。
(I)求证![]() ;
;
(II)求面ASD与面BSC所成二面角的大小;
(III)求SD与面SAB所成角的大小
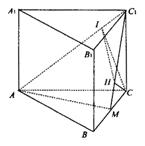
20、(本小题满分12分)如图,正三棱柱![]() 的底面边长为a,点M在边BC上,△
的底面边长为a,点M在边BC上,△![]() 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
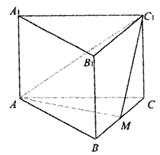
(1)求证点M为边BC的中点;
(2)求点C到平面![]() 的距离
的距离
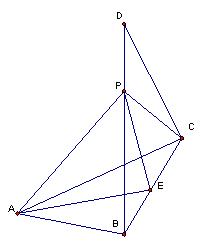
21、(本小题满分12分)⊿ABC是边长为2的正三角形,在⊿ABC所在平面外有一点P,PB=PC=![]() ,PA=
,PA=![]() ,延长BP至D,BD=
,延长BP至D,BD=![]() ,E是BC的中点,求AE和CD所成角的大小和这两条直线间的距离.
,E是BC的中点,求AE和CD所成角的大小和这两条直线间的距离.
22、如图,已知![]() 面
面![]() ,
,![]() 于D,
于D,![]() .
.
(1)令![]() ,
,![]() ,试把
,试把![]() 表示为
表示为![]() 的函数,并求其最大值;
的函数,并求其最大值;
(2)在直线PA上是否存在一点Q,使得 ![]() ?
?

 数 学 答 题 卷
数 学 答 题 卷
一、 选择题:请将唯一正确答案的编号填入答卷中,本题共12题,每题5分,共60分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:本题共4题,每题4分,共16分。
13_________________________ 14_________________________
15_________________________ 16_________________________
三、解答题:本题共6题,17、18、19、20、21题12分,22题14分,共74分。
![]() 17、
17、
18、
孟州五中05-06学年下学期高二年级期中考试卷
数学参考答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | A | B | A | D | A | D | D | C | D | A | D |
12.解 当l与异面直线a,b所成角的平分线平行或重合时,a取得最小值![]() ,当l与a、b的公垂线平行时,a取得最大值
,当l与a、b的公垂线平行时,a取得最大值![]() ,故选(D)
,故选(D)
二、填空题
13.钝角 14. 解:在长方体OXAY—ZBPC中,OX、OY、OZ是相交的三条互相垂直的三条直线。又PZ![]() OZ,PY
OZ,PY![]() OY,PX
OY,PX![]() OX,有 OX2+OZ2=49,OY2=OX2=9, OY2+OZ2=16,得 OX2+OY2+OZ2=37,OP=
OX,有 OX2+OZ2=49,OY2=OX2=9, OY2+OZ2=16,得 OX2+OY2+OZ2=37,OP=![]() 15.
15. ![]() 16.
16.![]()
17.证法一:分别过E、F作EM⊥AB于点M,FN⊥BC于点N,连结MN.
∵BB1⊥平面ABCD,
∴BB1⊥AB,BB1⊥BC.
∴EM∥BB1,FN∥BB1.∴EM∥FN.
又B1E=C
故四边形MNFE是平行四边形.
∴EF∥MN.又MN在平面ABCD中,
∴EF∥平面ABCD.
证法二:过E作EG∥AB交BB1于点G,连结GF,则![]() =
=![]() .
.
∵B1E=C![]() =
=![]() .
.
∴FG∥B
又∵EG∩FG=G,AB∩BC=B,
∴平面EFG∥平面ABCD.而EF在平面EFG中,
∴EF∥平面ABCD.
评述:证明线面平行的常用方法是:证明直线平行于平面内的一条直线;证明直线所在的平面与已知平面平行.
18.证明:,∵∠APE=∠APF=90°,PE∩PF=P,∴PA⊥平面PEF.
∵EF![]() 平面PEF,∴PA⊥EF.
平面PEF,∴PA⊥EF.
(2)证明:∵∠APE=∠EPF=90°,AP∩PF=P,∴PE⊥平面APF.又PE![]() 平面PAE,∴平面APE⊥平面APF.
平面PAE,∴平面APE⊥平面APF.
19. 分析:本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力、逻辑思维能力和运算能力。
(I)证明:
∵底面ABCD是正方形 ![]()
SD⊥底面ABCD ![]() DC是SC在平面ABCD上的射影
DC是SC在平面ABCD上的射影
由三垂线定理得![]()
(II)解:SD⊥底面ABCD,且ABCD为正方形
![]() 可以把四棱锥
可以把四棱锥![]() 补形为长方体
补形为长方体![]() ,如图2
,如图2
面ASD与面BSC所成的二面角就是面![]() 与面
与面![]() 所成的二面角,
所成的二面角,
![]()
又![]()
![]() 为所求二面角的平面角
为所求二面角的平面角
在![]() 中,由勾股定理得
中,由勾股定理得![]() 在
在![]() 中,由勾股定理得
中,由勾股定理得![]()
![]() 即面ASD与面BSC所成的二面角为
即面ASD与面BSC所成的二面角为![]()
(III)解45° 显然是∠DSA。过程不细说了,呵呵。
20. (1)∵ △![]() 为以点M为直角顶点的等腰直角三角形,∴
为以点M为直角顶点的等腰直角三角形,∴ ![]() 且
且![]() .∵ 正三棱柱
.∵ 正三棱柱![]() , ∴
, ∴ ![]() 底面ABC.
底面ABC.
∴ ![]() 在底面内的射影为CM,AM⊥CM.
在底面内的射影为CM,AM⊥CM.
∵ 底面ABC为边长为a的正三角形,∴ 点M为BC边的中点.
(2)过点C作CH⊥![]() ,由(1)知AM⊥
,由(1)知AM⊥![]() 且AM⊥CM,
且AM⊥CM,
∴ AM⊥平面![]() ∵ CH在平面
∵ CH在平面![]() 内, ∴ CH⊥AM,
内, ∴ CH⊥AM,
∴ CH⊥平面![]() ,由(1)知,
,由(1)知,![]() ,
,![]() 且
且![]() .
.
 ∴
∴ ![]() .
.
∴ 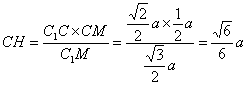 .
.
∴ 点C到平面![]() 的距离为底面边长为
的距离为底面边长为![]() .
.
21. (12分) 解:分别连接PE和CD,可证PE//CD,(1分)则∠PEA即是AE和CD所成角.(2分)在Rt⊿PBE中,
PB=![]() ,BE=1,∴PE=
,BE=1,∴PE=![]() 。在⊿AEP中,AE=
。在⊿AEP中,AE=![]() ,
,![]()
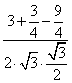 =
=![]() .
.
∴∠AEP=60º,即AE和CD所成角是60º.(6分)
∵AE⊥BC,PE⊥BC,PE//DC,∴CD⊥BC,∴CE为异面直线AE和CD的公垂线段,(10分)它们之间的距离为1.(12分)
22. 解:(1)为寻求![]() 与
与![]() 的关系,首先可以将
的关系,首先可以将![]() 转化为
转化为![]() .
.
∵ ![]() 面
面![]() ,
,![]() 于D,
于D,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]()
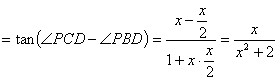 .
.
∵ ![]() 为
为![]() 在面
在面![]() 上的射影,
上的射影,
∴ ![]() ,即
,即![]() ,
,
∴ ![]()
 .
.
即![]() 的最大值为
的最大值为![]() ,等号当且仅当
,等号当且仅当![]() 时取得.
时取得.
(2)由正切函数的单调性可知:点Q的存在性等价于:是否存在点Q使得![]()
![]() ,
,
![]() ,
,
令![]()
![]()
![]() ,解得:
,解得:![]() ,与
,与![]() 交集非空,
交集非空,
∴ 满足条件的点Q存在.
