南昌十六中高二数学月考试卷

本试卷分第Ⅰ卷和第Ⅱ卷两部分，共150分.

题型	选择题	填空题	17题	18题	19题	20题	21题	22题	总分
得分

第Ⅰ卷（选择题，共60分）

一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1．若为正整数，则乘积（　　）

　　　A．　 　　　　　　　 B．　　　　　　　 C．　　  　　　 D．

2．若直线的系数同时从0,1,2,3,5,7六个数字中取不同的值,则这些方程表示不同的直线条数 （　　）

A． 22　　　　 　　　B． 30 　　　　　　 C． 12　　　　 　　　D． 15

3. 以平行六面体的顶点为顶点的三棱锥的个数是（　　）

A. 58　　 B. 70　　 C. 106　  D. 118

4．用0，1，2，3，4组成没有重复数字的全部五位数中，若按从小到大的顺序排列，则数字12340应是第几个数（　　）

　 A．6　　　　　　  　B．9　　　　　  C．10　　　　　  　　 D．8　

5.下列说法正确的是　（　　 ）

A、直线a平行于平面M，则a平行于M内的任意一条直线

B、直线a与平面M相交，则a不平行于M内的任意一条直线

C、直线a不垂直于平面M，则a不垂直于M内的任意一条直线

D、直线a不垂直于平面M，则过a的平面不垂直于M

6. 数11¹⁰⁰-1的末尾连续为零的个数是(　　)

A.0　　　　　　 B.3　　　　　　 C.5　　　　　　 D.7

7．把一个圆周24等分,过其中任意三个分点可以连成圆的内接三角形,其中直角三角形的个数是　（　　）

　　　A．2024　　　　　　　B．264 　　　　　　C．132　　　　　　　　D．122

8.若集合是从M到N的映射，则满足的映射有（　  ）

A．6个　　　　　 B．7个　　　　　 C．8个　　　　　  D．9个

9、设四次独立重复试验中，事件A最少发生三次的概率为 ，则在一次试验中事件A发生的概率为 （　　）

(A) 　　　　(B) 　　　　 (C) 　　　　 (D)

10、某厂有三个顾问，假定每个顾问发表的意见是正确的概率为0.8，现就某事可行与否征求各顾问的意见，并按顾问中多数人的意见作出决策，作出正确决策的概率是（　　）

(A) 0.896 　　 　　　(B)0.512　　　 　　　(C)0.64　　　　　  (D)0.384

11.有一名同学在书写英文单词“error”时，只是记不清字母的顺序，那么他写错这个单词的概率是 A.　　　　B.　　　　  C.　　　　D.

12．有10个均匀材料做成各面上分别标有数1，2，3，4，5，6的正方体玩具，每次同时抛出，共抛5次，则至少有一次全部都是同一个数字的概率为　　　　　　　　　　　　　　（　　）

A．[¹⁰]⁵　　　　B．[⁵]¹⁰C．1－[⁵]¹⁰　　　　D．1－[¹⁰]⁵

选择题	1	2	3	4	5	6	7	8	9	10	11	12

第Ⅱ卷（非选择题，共90分）

二、填空题：（每小题4分，共16分。把答案填在题中的横线上）

13．(2x²－3x－1）⁴展开式中x²项的系数是　　　　　　　　 

14．由0，1，2，3，4，5可以组成奇数与偶数相间且能被5整除的无重复数字的六位数的个数是　　　　　　　　  .

15．如图，一个地区分为5个行政区域，现给

地图着色，要求相邻区域不得使用同一颜色，

现有4种颜色可供选择，则不同的着色方法

共有　　　　　　　 种

16．将正整数n表示成k个正整数的和（不计较各数的次序），称为将正整数n分成k个部分的一个划分，一个划分中的各加数与另一个划分的各加数不全相同，则称为不同的划分，将正整数n划分成k个部分的不同划分的个数记为P（n，k），则P（10，3）＝______________．

三、解答题：（本大题共6道题共74分。请写出必要的文字说明和演算、推理步骤）

17．（本小题满分12分）如图，用A、B、C三类不同的无件连接成两个系统N₁、N₂，当元件A、B、C都正常工作时，系统N₁正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N₂正常工作，已知元件A、B、C正常工作的概率依次为0.80，0.90，0.90，分别求系统N₁、N₂正常工作的概率P₁、P₂.

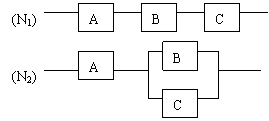18．（本小题满分12分）某学校有9名教师，其中4人只能教数学，3人只能教英语，2人既能教数学又能教英语.现要从中选出6人参加讲师团，必须有数学教师和英语教师各3人，有多少种不同的选法？

19. （本小题满分12分）

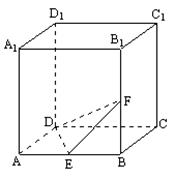
如图，正方体ABCD－A₁B₁C₁D₁中，E，F分别为AB与BB₁的中点，（1）求证：EF⊥平面A₁D₁B ； （2）求二面角F－DE－C大小．

20．（本小题满分12分）在一次三人象棋对抗赛里，甲胜乙的概率为0.4，乙胜丙的概率为0.5，丙胜甲的概率为0.6，比赛顺序如下：第一局，甲对乙；第二局，第一局的胜者对丙；第三局，第二局的胜者对第一局的败者；第四局，第三局的胜者对第二局的败者。计算：①乙连胜四局的概率；②丙连胜三局的概率.

21. （本小题满分12分） 三位数，若，则称为渐升数，若，则为渐降数，若，称为凸数，若，称为凹数，求四种数各有多少个。

22.（本小题满分14分） 甲、乙两人进行五次比赛，如果甲或乙无论谁胜了三次，比赛宣告结束。假定每次甲获胜的概率是，乙获胜的概率是，试求下列概率。（I）比赛以甲3胜1败而结束的概率；（II）比赛以乙3胜2败而结束的概率；（III）设最终甲获胜的概率为a，乙获胜的概率为b，求a：b的值。

高二数学月考试卷参考答案

1.D 2.A 3. A 4.C 5.B 6.B 7.B 8.B 9.B 10.A 11.C 12.D　 13.46  14.20  15.72　16.8

17．分别记元件A、B、C正常工作的事件A、B、C，由已知

P₁=P（A·B·C）=P（A）·P（B）·P（C）=0.8×0.9×0.9=0.648

故系统N₁正常工作的概率为0.648…………………………………………………………………6分

P₂=P（A）·[1－P（=0.80×(1－0.10×0.10)=0.80×0.99=0.792

故系统N₂正常工作的概率为0.792.………………………………………………………………12分

18．对于既能教数学又能教英语的2人有以下三种情况

（1）都不选，有=4种…3分　　 （2）都选，有=52种…7分

（3）只选一人，有=36种…10分 所以共有4+52+36=92种不同的选法…12分

19. （本小题满分12分）　（1）

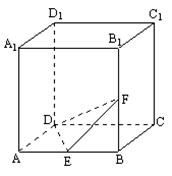
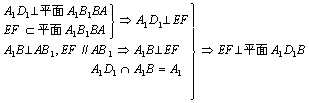
（II）延长DE、CB交于N，∵E为AB中点，

∴△DAE≌△NBE

过B作BM⊥EN交于M，连FM，∵FB⊥平面ABCD

∴FM⊥DN，∴∠FMB为二面角F—DE—C的平面角 

设AB=a，则BM=　　又BF=

∴tan∠FMB=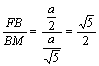，　　即二面角F—DE—C大小为arctan　　 

证明二（向量法）：（1）以射线、、分别为OX、OY、OZ轴，建立空间直角坐标系，设正方体ABCD－A₁B₁C₁D₁棱长为2，则E（2，1，0），F（2，2，1），A₁（2，0，2），D₁（0，0，2），B（2，2，0）；=（0，1，1），=（-2，0，0），=（0，2，-2）.

　　　　　　　　 由•=0，•=0 ，可得 EF⊥A₁D₁，　　EF⊥A₁B，∴EF⊥平面A₁D₁B（2）平面CDE的法向量为=（0，0，2），设平面DEF的法向量为

 =（x，y，z），由•=0，•=0 ，解得2 x= - y=z，

可取 =（1，-2，2），设二面角F－DE－C大小为θ，

∴cosθ=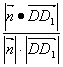==，即二面角F—DE—C大小为arccos

20．①乙连胜四局，必须每局乙都是胜者，则P₁=0.6×0.5×0.6×0.5=0.09

　　即乙连胜四局的概率为0.09…………………………………………………………………………5分

②由于第一局的胜者不同，丙连胜三局有两种情况，则0.4×0.6×0.5×0.6+0.6×0.5×0.5×0.6=0.162

即丙连胜三局的概率为0.162……………………………………………………………………12分

21.解：规定顺序即设有顺序

（1）………………2分　（2）（无0）………………4分

（3）讨论1，2，3……9　　…………8分

（4）讨论0，1，2……9　　………………12分

 22. 解：（I）以甲3胜1败而结束比赛，甲只能在1、2、3次中失败1次，因此所求概率为：

　　……4分 （II）乙3胜2败的场合，因而所求概率为：

　　………8分

　　（III）甲先胜3次的情况有3种：3胜无败，3胜1败，3胜2败

　　其概率分别为　　于是………11分

　　乙获胜概率　 　　 ……………14分