2005-2006学年第一学期南昌市期末考试试卷
数学(普通中学)
一、选择题(每题3分,共10题)
1.下列各命题中正确的是( )
![]()
![]()
![]()
![]()
2. 过(0,2)和(1,1)两点的直线的倾斜角是( )
A 150 0 B 1350 C 900 D 450
3.![]() ( )
( )
![]()
![]()
![]()
![]()
4.![]() ( )
( )
![]()
![]()
![]()
![]()
5.以点 ![]() 为圆心的圆与直线
为圆心的圆与直线
![]() 相离,则圆的半径
相离,则圆的半径
![]() 的取值范围是(
)
的取值范围是(
)
![]()
![]()
![]()
![]()
6.![]()
![]()
![]()
![]()
![]()
![]()
![]()
7.![]() ( )
( )
![]()
![]()
![]()
![]()
8.![]()
![]()
![]()
![]()
![]()
9.![]() ( )
( )
![]()
![]()
![]()
![]()
10.![]()
![]()
![]()
![]()
![]()
二.填空题(5题共20分)
11.![]() 为
。 12.
为
。 12.![]() 的
的
![]() 。
。
13.![]()
![]() 。
。
14.![]()
为
15. 对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;②焦点在x轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④抛物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).能使这抛物线方程为![]() 的条件是
(要求填写合适条件的序号).
的条件是
(要求填写合适条件的序号).
三、解答题
16. (本小题满分8分) 已知椭圆![]() ,其长轴长是短轴长的2倍,右准线方程为
,其长轴长是短轴长的2倍,右准线方程为![]() .求该椭圆方程,
.求该椭圆方程,
17. (本小题满分10分)已知a≠0且a≠-2,解关于x的不等式:
a(![]() +1)> x+2
+1)> x+2
18. (本小题满分10分)自点(-3,3)发出的光线L射到x轴上,被x轴反射,其反射线所在直线与圆![]() 相切,求光线L所在直线方程.
相切,求光线L所在直线方程.
19. (本小题满分10分)已知抛物线 y 2 = – x与直线 y = k ( x + 1 )相交于A、B两点, 点O是坐标原点.
(1) 求证: OA^OB;
(2) 当△OAB的面积等于![]() 时, 求k的值
时, 求k的值
20. (本小题满分12分)已知双曲线![]() 及点P(2,1),是否存在过点P的直线l,使直线l被双曲线截得的弦恰好被P点平分?若存在,求出直线l的方程;若不存在,请说明理由。
及点P(2,1),是否存在过点P的直线l,使直线l被双曲线截得的弦恰好被P点平分?若存在,求出直线l的方程;若不存在,请说明理由。
答案:
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | C | B | C | D | C | A | A | D |
二、填空题
11.x+3y+1=0 12.(x-2)2+(y-4)2=10 13. ![]()
14.y2=16x 15. ②⑤
三、解答题
16. 解: ![]() 2分
2分
∴![]() 4分
4分
又![]() 6分
6分
![]() 8分
8分
17. 解:∵a(![]() +1)> x+2 ∴a(
+1)> x+2 ∴a(![]() +1)-x-2>0
1分
+1)-x-2>0
1分
∴![]() 2分
2分
∴![]() 4分
4分
![]() 6分
6分
∴原不等式等价于x(x+2)(x-a)<0 7分
①当a>0时,其解集为![]() 8分
8分
②当-2<a<0时,其解集为![]() 9分
9分
③当a<-2时,其解集为![]() 10分
10分
18. 解:已知圆的标准方程是![]()
它关于x轴的对称圆的方程是![]() 2分
2分
设光线L所在直线方程是![]() 3分
3分
由题设知对称圆的圆心C′(2,-2)到这条直线的距离等于1,
即![]() .
6分
.
6分
整理得![]()
解得![]() .
8分
.
8分
故所求的直线方程是![]() ,或
,或![]() ,
,
即3x+4y-3=0,或4x+3y+3=0. 10分
19.解: (1) 当k = 0时直线与抛物线仅一个交点, 不合题意, 1分
∴k ¹ 0由y = k
(x+1)得x = ![]() –1 代入y 2 = – x
–1 代入y 2 = – x
整理得: y
2 +![]() y – 1 = 0 ,
3分
y – 1 = 0 ,
3分
设A(x1 , y1),B(x
2,y 2) 则y1+y2 =–![]() , y1y 2 =–1. 4分
, y1y 2 =–1. 4分
∵A、B在y 2 = – x上, ∴A (–![]() , y 1 ), B (–
, y 1 ), B (–![]() , y 2 ) ,
, y 2 ) ,
∴ kOA·kOB =![]() =
=![]() = – 1 .
= – 1 .
∴ OA^OB. 6分
(2) 设直线与x轴交于E, 则 E ( – 1 , 0 ) ∴OE = 1 ,
S△OAB =![]() OE( y 1 + y 2 ) =
OE( y 1 + y 2 ) =![]() y 1 – y 2 =
y 1 – y 2 =![]()
![]() =
=![]() , 8分
, 8分
解得k = ±![]() .
10分
.
10分
20. 解:假设符合题意的直线l存在. ……1分
设直线l与双曲线的两个交点分别为![]() .
.
∴ ……5分
……5分
∵P(2,1)为AB的中点,
∴![]() ……7分
……7分
∴![]() .
……8分
.
……8分
∴直线![]() 的方程为
的方程为![]() ……10分
……10分
但由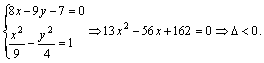 ……11分
……11分
∴不存在符合题意的直线l. ……12分