南昌市2005-2006学年度第一学期期末终结性测试卷
高 二 数 学 (重点)
|
大题号 | 一 | 二 | 三 | 总总分 | ||||
| 16 | 17 | 18 | 19 | 20 | ||||
| 满分值 | 30 | 20 | 8 | 10 | 10 | 10 | 12 | |
| 实得分 | ||||||||

一、选择题(本大题共10小题,每小题3分,共30分)在每小题得出的四个结论中,
只有一项是符合题目的要求,把正确结论的代号填入题后的答题表
1.已知椭圆方程为![]() ,则这个椭圆的焦距为
( )
,则这个椭圆的焦距为
( )
A.6 B.3 C.![]() D.
D.![]()
2. 空间四点中,无三点共线是四点共面的 ( )
A.充分不必要条件 B.必要不充分条件C.充分必要条件 D.既不充分也不必要
3. 已知正方体ABCD-A1B1C1D1的棱长为a,则棱A1B1
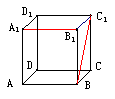 所在直线与面对角线BC1所在直线间的距离是 ( )
所在直线与面对角线BC1所在直线间的距离是 ( )
A.![]() B .
B .![]()
![]() C
C![]() D.
D.![]()
![]()
4.到直线![]() 的距离为
的距离为![]() 的点的集合是 (. )
的点的集合是 (. )
A. ![]() B.
B. ![]()
C. ![]() 或
或![]() D
D![]() .或
.或![]()
5.下列说法不正确的是 ( )
(1)一条直线垂直于一个平面内的无数条直线,则这条直线和这个平面垂直;
(2)经过一点和一条已知直线垂直的直线都在同一平面内;
(3)一个平面内不可能有直线与这个平面的一条斜线垂直;
(4)如果直线a//平面α,直线b⊥a,则b⊥平面α。
A .(2) B.(1)(3) C.(1)(2)(3) D.( 1)(3)(4)
6.直线过点(0,2),且被圆![]() 截得的弦长为2,则此直线的斜率是
截得的弦长为2,则此直线的斜率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() ( )
( )
7 .已知点(3,1)和(-4,6)在直线![]() 的两侧,则
的两侧,则![]() 的取值范围为( )
的取值范围为( )
- 1 -
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设![]() 为椭圆
为椭圆![]() 上一点,
上一点,![]() 、
、![]() 为焦点,如果
为焦点,如果![]() ,
,![]()
则椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
9.过抛物线![]() 的焦点的直线交抛物线于A、B两点,O为坐标原点,则
的焦点的直线交抛物线于A、B两点,O为坐标原点,则![]() 的值是
的值是
A.3 B.-3 C.12 D.-12 ( )
10.两双曲线![]() 的离心率分别为
的离心率分别为![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.![]() B.2
C.
B.2
C.![]() D. 4
D. 4
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(本大题共5小题,每小题4分,共20分)把答案填在题中的横线上.
11. 过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 两点,如果
两点,如果![]() ,那么
,那么![]() =
.
=
.
12.过点(3,-2)且与椭圆![]() 有相同焦点的椭圆方程是
.
有相同焦点的椭圆方程是
.
13. 双曲线的两条渐近线为![]() ,则它的离心率为
.
,则它的离心率为
.
14. A、B两点到平面α的距离分别是3、5,M是的AB中点,则M到平面α的距离是
 .
.
15.右图是正方体平面展开图,在这个正方体中
①![]() 与
与![]() 垂直; ②
垂直; ②![]() 与
与![]() 垂直.
垂直.
③![]() 与
与![]() 成60º角; ④
成60º角; ④![]() 与
与![]() 是异面直线
是异面直线
以上四个命题中,正确命题的序号是 .
三、解答题 (本大题共5小题,共50分)解答应写出文字说明
、演算步骤或证明过程.
16.(本题满分8分)椭圆![]() ,其上一点P(3,
,其上一点P(3,![]() )到两焦点的距离分别6.5和3.5 ,求椭圆方程
)到两焦点的距离分别6.5和3.5 ,求椭圆方程![]()
- 2 -
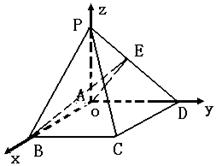
17.(本题满分10分)如图所示直角梯形![]() 中,
中,![]() ,
,![]() 面
面![]() ,
,![]() ,
,

![]() ,
,![]() 与底面
与底面![]() 成
成![]() 角
角
(1)若![]() 为垂足,求证:
为垂足,求证:![]() .
.
(2)求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
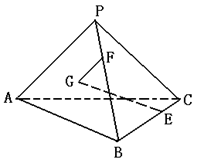
18.(本题满分10分)如图,![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,![]() ,
,![]() 是△
是△![]() 的重心,
的重心,![]() 是
是![]() 上的一点,且
上的一点,且![]() =
=![]()
![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() =
=![]()
![]()
(1)求证: ![]() 平面
平面![]() ;(2)求证:
;(2)求证:![]() ^平面
^平面![]() .
.
- 3 -
19.(本题满分10分)河上有一抛物线型拱桥,当水面距拱顶5米时,水面宽为8米,一小船宽4米,高2米,载货后船露出水面上的部分高为![]() 米,问水面上涨到与抛物线拱顶相距多少米时,小船不能通航?
米,问水面上涨到与抛物线拱顶相距多少米时,小船不能通航?
20.(本题满分12分)设双曲线的顶点是椭圆![]() 的焦点,该双曲线又与直线
的焦点,该双曲线又与直线![]() 交于两点A、B且
交于两点A、B且![]() (O为原点)(1)求此双曲线的标准方程 (2)求
(O为原点)(1)求此双曲线的标准方程 (2)求![]() 的长度.
的长度.
- 4 -
参考答案
一。选择题
1.A 2.D 3.A 4.D 5.D 6.B 7.C 8.B 9.B 10.C
二.填空题
11. 8 12. ![]() 13
13![]() 14. 1或4
15. ① ② ③
14. 1或4
15. ① ② ③
三、解答题
16. 解:由椭圆的焦半径公式,得
![]() ,解得
,解得![]() , ……(4分)
, ……(4分)
从而有 ![]() …….(6分)
…….(6分)![]()
所求椭圆方程为 ![]() ………(8分)
………(8分)![]()
17. 解:(1) ![]()
![]() 面
面![]() ,
,![]() ,如图建立空间坐标系
,如图建立空间坐标系
![]()
![]() ……..(2分)
……..(2分)
![]() ……(4分)
……(4分)
![]()
![]() ……(5分)
……(5分)
(2)![]()
![]() ,
,![]() ……(6分)
……(6分)
设![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
则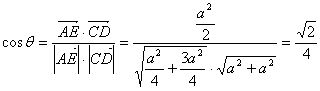 ……(9分)
……(9分)
故异面直线![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() ……(10分)
……(10分)
18. 证明:(1)连结![]() 和
和![]() ,并延长分别交
,并延长分别交![]() 、
、![]() 于
于![]() 和
和![]() ,连结
,连结![]()
在△![]() 中,∵
中,∵![]() 是△
是△![]() 的重心,∴
的重心,∴![]() =
=![]()
![]() ,
,
又![]() ,所以在△
,所以在△![]() 中
中![]()
![]() ……(3分)
……(3分)
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ………(5分)
………(5分)
 (2)在△
(2)在△![]() 中,∵
中,∵![]() 是△
是△![]() 的重心,
的重心,
∴![]() =
=![]()
![]() ,
,![]()
![]() =
=![]()
![]()
∴![]() ∥
∥![]() …………(7分)
…………(7分)
又![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,
∴![]() ^平面
^平面![]() ,则
,则![]() ^平面
^平面![]() ………(10分)
………(10分)
19. 解:如图建立坐标系,
设抛物线方程为![]()
由题意将点![]() 代入方程得
代入方程得![]() ……(4分)
……(4分)
所以抛物线的方程为![]() ………(5分)
………(5分)
船面两侧和抛物线桥接触时,船不能通航,设此时的船面宽为![]()
 则
则![]() , 由
, 由![]()
![]() ………(8分)
………(8分)
又知船面露出水面的部分为![]() 米,
米,
![]() 米……(9分)
米……(9分)
答:水面上涨到距抛物线拱桥拱顶2米时,小船不能通航 …… (10分)
20.解答:(1)椭圆![]() 的焦点为
的焦点为![]() ,
,
依题意设双曲线的方程为![]() ………(2分)
………(2分)
设![]() ,则
,则![]() ,
,![]()
![]() ,
,![]()
由 ![]()
![]()
![]() ……①
…………….(4分)
……①
…………….(4分)
由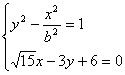
![]() …②
…②
![]() …………(6分)
…………(6分)
代入①中得![]()
![]() 双曲线的方程为
双曲线的方程为![]() ……(8分)
……(8分)
(2)将![]() 代入②式中,得
代入②式中,得![]()
![]() ………(10分)
………(10分)
![]()
![]() ……(12分)
……(12分)