南京九中高二数学期末测试模拟

班级_______________姓名______________________

一、选择题(每题5分,共60分)

1、教室内有一直尺，无论怎样放置，在地面总有直线与直尺所在直线　　　　　  (　　)

 A、平行　　　　  B、垂直　　　　  C、相交　　　　  D、 异面

2、过点（2,1）的直线中，被截得的最长弦所在的直线方程是　 （　　）

A、3x-y-5=0　　B、3x+y-7=0　　　 C、x+3y-5=0　　 D、x-3y+1=0

3、已知是三角形的一个内角，且，则方程表示（　　）

  A、焦点在轴上的椭圆　　　　　　　　  B、焦点在轴上的椭圆

　C、焦点在轴上的双曲线　　　　　　　  D、焦点在轴上的双曲线

4、已知直线，与轴，轴所围成的四边形有外接圆，则实数的值是　　　　　　 　　　　 (　　)

 A、　　　　  B、　　　　  C、　　　　  D、

5.设三棱锥的顶点在平面上的射影是，给出以下命题：

①若，，则是的垂心

②若两两互相垂直，则是的垂心

③若，是的中点，则

④若，则是的外心

其中正确命题的命题是　　 　　　　　　

A、1　　　　　　 B、2  　　　　　 C、3　　　　　　 D、4

6、设F₁、F₂是双曲线的两个焦点，点P在双曲线上，∠F₁PF₂=90°若△F₁PF的面积为1，则a的值是　　　 （　　）

A、1　　　　　  B、　 　　　C、2　　　　　  D、

7、与圆：相切且在、轴上截距相等的直线有　　　 (　　)

 A、条　　　　 B、条　　　　 C、条　　　　  D、条

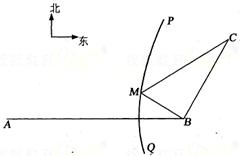
8、如图，B地在A地的正东方向4 km处，C地在B地的

北偏东30°方向2 km处，河流的没岸PQ（曲线）上任意

一点到A的距离比到B的距离远2 km.现要在曲线PQ上选

一处M建一座码头，向B、C两地转运货物。经测算，从

M到B、M到C修建公路的费用分别是a万元/km、

2a万元/km，那么修建这两条公路的总费用最低是 （　　）

A、(2－2)a万元　B、5a万元　C、(2+1)a万元 　D、(2+3)a万元

9、直线与圆的位置关系是　　　　　　　　 (　　)

  A、相交　　　　 B、相离　　　　 C、相切　　　　D、与、的取值有关

10．AB、CD在平面α内，AB//CD，且AB与CD相距28厘米，EF在平面α外，EF//AB，且EF与AB相距17厘米，EF与平面α相距15厘米，则EF与CD的距离为（　　　 ）

25厘米　　  39厘米　　　 25或39厘米　　15厘米

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　

11．已知直线a，如果直线b同时满足条件：①a、b异面②a、b所成的角为定值③a、b

间的距离为定值，则这样的直线b有（　　　　　）

1条　　　　 2条　　　　  4条　　　　　  无数条

12．已知异面直线a与b所成的角为50⁰，P为空间一点，则过点P与a、b所成的角都是30⁰的直线有且仅有（ 　　　　　 ）

1条　　　　2条　　　　  3条　　　　　  4条

13、给出下列四个命题：①若，则；②若、，则；

③若、，则；④若、、，则。其中真命题的序号是　　　　　　　  （　　）

　A、①③　　　　B、②③　　　　C、①②③　　　　D、①②③④

14、双曲线的两个焦点为，以为边作等边三角形，若双曲线恰平分三角形的另两边，则双曲线的离心率为　　　　　 （　　）

A、　　  　B、　　  　C、　　 　D、

二、填空题(每题4分,共16分)

 15、已知正方体的棱长为1，则过A₁C₁且与BD₁平行的截面面积为___________。

16、已知椭圆E的离心率为e，两焦点为F₁、F₂，抛物线C以F₁为顶点，F₂为焦点，P为两曲线的交点，若，则e的值为___________。

17、直线的方程为，在上任取一点P，若过点P且以双曲线的焦点作为椭圆的焦点，那么具有最短长轴的椭圆方程为________________________。

18、正方形ABCD的两对角线AC与BD交于O，沿对角线BD折起，使∠AOC=90对于下列结论：①AC⊥BD；②△ADC是正三角形；③AB与CD成60角；④AB与平面BCD成60角，其中正确的结论是_____________________。

三、　　　　　　 解答题(17题10分,18,19,20题各12分,21,22题各14分)

19..抛物线C：=2 （＞0）与直线：=＋m相交于A、B两点，

线段AB的中点横坐标为5，又抛物线C的焦点到直线的距离为，

试求,m的值。　　　　   

20．如图是所在平面外一点，平面，是的中点，

是上的点，

（1）求证：；（2）当，时，求的长。

21、过点A(1,0)的直线与y轴交于点M，在直线上取一点N，使得MN=AMAN。

(1)　  求点N的轨迹方程；

(2)　  直线与(1)中的曲线交于C、D两点，若OC=CD，求此直线方程。

 

 

22、在棱长为4的正方体ABCD-A₁B₁C₁D₁中，O是正方形A₁B₁C₁D₁的中心，点P在棱CC₁上，且CC₁=4CP。

(1)　  求直线AP与平面BCC₁B₁所成的角的大小(结果用反三角函数值表示)；

(2)　  设点O在平面D₁AP上的射影是H，求证：D₁H⊥AP；

(3)　  求点P到平面ABD₁的距离。

23、已知椭圆C： 的焦点在坐标轴上，A为右顶点，射线与椭圆的交点为B。

(1)　  写出以R(m，0)为顶点，A为焦点，开口向左的抛物线方程；

(2)　  当点B在抛物线上，且椭圆的离心率满足时，求m的取值范围。

24．如图棱长是1的正方体，P、Q分别是棱AB、CC₁上的点，且.

（1）求证：A₁P⊥平面AQD；

（2）求直线PQ与平面AQD所成角的正弦值.

参考答案：BABBB，ACBAD，CA

13、，14、，15、，16.1,3  17.略　

18.（1）证明：取的中点，连结，∵是的中点，

　 ∴，∵ 平面 ，∴　平面　　　　　　　　　　　　　

　∴是在平面内的射影 ，取 的中点，连结　　　　　　　　　　　 

 ，∵∴，又，∴

∴，∴，由三垂线定理得

（2）∵，∴，∴，∵平面

∴，且，∴

19.（1）证明：设：，

由方程组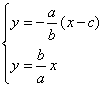得，

∵成等比数列，∴，

∴，，，

∴，，∴．

（2）设，

由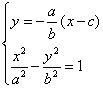得，

∵，∴，∴，即，∴．

20、 (1)

21、(1) ，(3)，22、。