解析几何同步练习（椭圆及其标准方程1A）

知识要点：　　　 ①定义：；

　　　　　  ②标准方程：；。

一、选择题

1、若点P到两定点F₁（-4，0），F₂（4，0）的距离和是8，则动点P的轨迹为　　[　 ]

A.椭圆　　　　　　B.线段F₁F₂　 　　　 C.直线F₁F₂　 　　　 D.不能确定

2.下列说法正确的个数是　　　　　　　　　　　　　　　　　　　　　　　　 [　 ]

①平面内与两个定点F₁、F₂的距离和等于常数的点的轨迹是椭圆②与两个定点F₁、F₂的距离的和等于常数（大于 F₁F₂）的点的轨迹是椭圆③方程（a>c>0）表示焦点在x轴上的椭圆④方程（a>0,b>0)表示焦点在y轴上的椭圆

A．1　　　　　　　B.2　　　　　　　　 C.3　　　　　　　　 D.4

3.椭圆的焦距为2，则m的值等于 　　　　　　　　　　　　　　 [　 ]

A.5或3　　　　　 B.8 　　　　　　　　C.5　　　　　　　　 D.16

4.过点（3，-2）且与有相同焦点的椭圆是　 　　　　　　　　　 [　 ]

A. 　　B. 　 C. 　　　D.

5．已知方程表示焦点在轴上的椭圆，则的取值范围是　　　　　  [　 ]

A．m<1　　B．-1<m<1　　C．m>1　 D．0<m<1

6.椭圆ax²+by²+ab=0（a<b<0）的焦点坐标是 　　　　　　　　　　　　　　　 [　 ]

A.（　 B.（0，）　C.（，0）　D.（0，）

二、填空题

7.如果椭圆上一点P到焦点F₁的距离等于6，则点P到另一个焦点

F₂的距离是　　　　　　  ；

8过椭圆C：的焦点引垂直于轴的弦，则弦长为　　　　

三、解答题：

9．求经过点A(0,2)和B()的椭圆的标准方程

10.椭圆的两个焦点F₁、F₂在x轴上，以 F₁F₂为直径的圆与椭圆的一个交点为（3，4），求椭圆标准方程.

11．已知点Ｐ在以坐标轴为对称轴的椭圆上，点Ｐ到两个焦点的距离分别为，过Ｐ作焦点所在轴的垂线恰好过椭圆的一个焦点，求椭圆的方程

参考答案

一、选择题：　 BAAA　DD

二、填空题：

1、14；　2、。

三、解答题

1、；　　　　　　 2、；　　　3、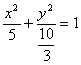；。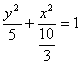