解析几何直线综合85（1）

一、选择题　　　　

1、

ΔPQR的顶点P(2，-4)，Q(-1，2)，R(3，4)，则ΔPQR的面积是　　(　　)

　  (A)12　　　　　　 (B)18　　　　　  (C)15　　　　　  (D)24

翰林汇

2、

在线段BA的延长线上，取点P，使，则P分AB的比为(　　)

　　(A)-　　　　　　 (B)-　　　　　　  (C)　　　　　　  (D)

翰林汇

3、

两条直线2x-y＋k=0和4x-2y＋1=0的位置关系是　　　　　　　　　 (　　)

　　(A)平行　　　 ( B)垂直　　　 (C)相交但不垂直　 　　(D)平行或重合

翰林汇

4、

已知点M(0，-1)，点N在直线x-y＋1=0上，若直线MN垂直于直线x＋2y-3=0，则点N坐标是　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

　　(A)(-2，-3)　　　　 (B)(2，1)　　　　　  (C)(2，3)　　　　(D)(-2，-1)

翰林汇

5、

两平行直线3x＋2y－3=0与6x＋ky＋1=0的距离为　　　　　　　  (　　)

(A)　　　　(B)　 　　　 (C)　 　　 (D)与k值有关

翰林汇

6、

三角形中， 已知三边a,b,c依次所对应的三内角α,β,γ满足lgsinα+lgsinγ=2lgsinβ, 则直线xsin²α+ysinα=α与xsin²β+ysinγ=c的位置关系是 (　　)

(A)　平行　　　  (B)　斜交　　　　 (C)　垂直　　　　  (D)　重合

翰林汇

7、

点(a,b)关于直线x+y=0对称的点是　　　　　　　　　　　　　　  (　　)

(A) (－a,－b) 　　　 (B)  (a,－b)　　　 　(C) (b,a) 　　　 (D) (－b,－a)

翰林汇

8、

已知l 平行于直线3x+4y－5=0, 且l和两坐标轴在第一象限内所围成三角形面积是24,则直线l的方程是　　　　　　　　　　　　　　　　　　　 (　　)

(A) 3x+4y－12=0 　　　　　　　　　　　　 (B) 3x+4y+12=0

(C) 3x+4y－24=0　　　　　　　　　　　　　　  (D) 3x+4y＋24=0

翰林汇

9、

点(4,0)关于直线5x+4y+21=0对称的点是　　　　　　　　　　　　　 (　　)

(A)　(－6,8)　　　(B)　(－8,－6)　　　 (C) (6,8)　　　  (D)　(－6,－8)

翰林汇

10、

若直线l经过点(1,1),且与两坐标轴所围成的三角形的面积为2,则直线l的条数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

(A)1　　 　　　　　 (B)2　 　　　　　 (C)3　　　　　　　　(D)4

翰林汇

11、

平面上两点A(4cosa，4sina)与B(3cosb，3sinb)之间的距离的最大值与最小值顺序为　　　　　　　　 　　　　　　　　　　　　　　　　　　　　 (　　)

　　(A)7与1　　　　  (B)6与1　　　　  (C)7与2　　 　　(D)6与2

翰林汇

12、

直线x+y-1=0的倾斜角为　　　　　　　　　　　　　　　　　  (　　)

　　　　(A)

翰林汇

13、

经过点A（－3，2）和B（6，1）的直线与直线x＋3y－6=0相交于M，M分所成的比是　　　　　　　　　　　　　　　　　　　　　　　  (　　)

（A）－1　　　　  （B）　　　　　 （C）1　　　　　  （D）2

翰林汇

14、

如图所示，直线l₁：ax－y＋b=0与l₂：bx－y＋a=0(ab≠0,a≠b)的图象只可能是(　　)

　　　　　　  　　  

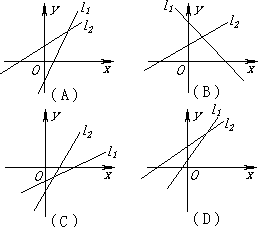
翰林汇

15、

由方程=1确定的曲线所围成的图形面积是　　　　　  (　　)

（A）1　　　　  （B）2　　　　　 （C）　　　　  （D）4

翰林汇

16、

一平行于y轴的直线把顶点为(0,0)、(1,1)、(9,1)的三角形分成面积相等的两部分，那么这条直线是　　　　　　　　　　　　　　　　　　　　　 (　　)

（A）x=2.5　 　　（B）x=3　　　（C）x=3.5　 　　（D）x=4

翰林汇

17、

经过原点，且倾斜角是直线y=x＋1倾斜角2倍的直线是　　　  (　　)

（A）x=0　　　 （B）y=0　　　　（C）y=x　 　（D）y=2x

翰林汇

18、

已知菱形的三个顶点为（a,b）、（－b,a）、（0，0），那么这个菱形的第四个顶点为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

（A）(a－b,a＋b)　　 （B）(a＋b, a－b)　　 （C）(2a,0)　　 （D）(0,2a)

翰林汇

19、

直线kx－y=k－1与ky－x=2k的交点位于第二象限，那么k的取值范围是(　　)

（A）k＞1　　 （B）0＜k＜　　  （C）k＜ 　　（D）＜k＜1

翰林汇

20、

直线ax＋by=ab(a＞0,b＜0)的倾斜角等于　　　　　　　　　　　  (　　)

（A）－arctg(－)　 　　　　　　　　　　　 （B）－arctg

（C）arctg(－)　　　　　　　　　　　　　　　（D）arctg

翰林汇

21、

下列命题中不正确的是　　　　　　　　　　　　　　　　　　　　  (　　)

（A）二直线的斜率存在时，它们垂直的充要条件是其斜率之积为－1

（B）如果方程Ax＋By＋C=0表示的直线是y 轴，那么系数A、B、C满足A≠ 0,B=C=0

（C）ax＋by＋c=0和2ax＋2by＋c＋1=0表示两条平行直线的充要条件是a²＋b²≠0且c≠1

（D）(x－y＋5)＋k(4x－5y－1)=0表示经过直线x－y＋5=0与4x－5y－1=0的交点的所有直线。

翰林汇

22、

过定点P(2,1)作直线l,交x轴和y轴的正方向于A、B，使△ABC的面积最小，那么l的方程为　　　　　　　　　　　　　　　　　　　　　　　  (　　)

(A)x-2y-4=0　　　 (B)x-2y+4=0　　　 (C)2x-y+4=0　　　 (D)x+2y-4=0

翰林汇

23、

△ABC的一个顶点是A(3,-1),∠B、∠C的平分线分别是x=0,y=x，则直线BC的方程是　　　　　　　　　　　　　　　　　　　　　　　　　　 ( 　 )

(A)y=2x+5　　　　(B)y=2x+3　 　　　(C)y=3x+5　 　　　(D)y=-

翰林汇

24、

若0<q<，当点(1，cosq)到直线：xsinq＋ycosq=1的距离为时，直线的斜率是　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

　　(A)1　　　　　　  (B)-1　　　　　　  (C)-　　　　　　 (D)

翰林汇

25、

已知两点A(-1，3)，B(3，1)，点C在坐标轴上，若ACB=60⁰，则点C有(　　)

　　(A)1个　　　　　 (B)2个　　　　　  (C)3个　　　　　　  (D)4个

翰林汇

二、填空题　　　　

1、

直线l经过点P（3，－1），且到直线y=2x的角等于45⁰，则l的方程是________

翰林汇

2、

直线l的斜率为－,且与两坐标轴所围成的三角形的周长等于24,则直线l的方程是________.

翰林汇

3、

△ABC的三个顶点分别为A(1,2),B(3,4),C(2,5),作平行于AB的直线l分别交AC、BC于D、E,且△CDE的面积等于△ABC的面积的一半,则直线l的方程是________.

翰林汇

4、

等腰直角三角形的斜边所在直线的方程是3x－y+2=0,直角顶点为C(3,－2),则两条直角边所在直线的方程是________.

翰林汇

5、

已知等腰直角三角形的两个顶点为A(3,0),B(0,4),则直角顶点C的坐标是____.

翰林汇

6、

设直线5x+4y=2m+1与2x+3y=m相交,且交点在第四象限内,则m的取值范围是________.

翰林汇

7、

直线l经过点(1,2),且和两坐标轴所围成的三角形是等腰直角三角形,则直线l的方程是________.

翰林汇

8、

已知直线l在x轴上的截距为－2,倾斜角满足,则直线l的方程是________.

翰林汇

9、

三条直线：2y=x+a,y=bx+4,cy=dx+1围成一个三角形,已知这三角形的两个顶点的坐标为(0,6),(2,0),则a=____,b=____,c=____,d=____.

翰林汇

10、

已知△ABC的顶点为A(0,0)B(3,0),C(1,2),则△ABC的重心坐标为________,垂心坐标为________,外心坐标为________.

翰林汇

三、计算题　　　　

1、

光线通过点A(－2,4), 经直线2x－y－7=0反射. 若反射线通过点B(5,8), 求入射线和反射线所在直线的方程.

翰林汇

2、

求点P（2，3）关于直线l：2x－y－4=0的对称点Q.

翰林汇

3、

已知直线l的方程为3x+4y－12=0, 求直线l^′的方程, 使得：

(1) l^′与l平行, 且过点(－1,3) ;

(2) l^′与l垂直, 且l^′与两轴围成的三角形面积为4.

翰林汇

4、

光线由点P(－1,3)射出, 遇直线x+y+1=0即行反射, 已知反射光线经过Q(4,－2), 求反射线所在直线方程.

翰林汇

5、

在直线3x－y－1=0上求一点M, 使它到点A(4,1)和B(0,4)的距离之差最大, 并求此最大值..

翰林汇

四、解答题　　　　

1、

根据下列条件，选用恰当的形式，写出直线的方程，并化为一般式：

经过点(0,－2)和(3,0).

翰林汇

2、

直线l经过A（3，2）点，斜率k=2，求l和x轴的交点P、和y轴的交点Q的坐标。

翰林汇

3、

直线l₁的斜率是，直线l₂的斜率是，直线l₃的倾斜角等于l₁，l₂的倾斜角的和，求l₃的斜率。

翰林汇

4、

的三个顶点分别是A，B（－1，3），C（3，－5），过A作直线l交BC边于D，若的面积是面积的，求l的方程。

翰林汇

5、

已知的三个顶点为A（2，－1），B（4，3），C（3，－2）

（1）求AC边上的高所在直线的方程；（2）求的三个内角。

翰林汇

6、

过点P(0,1)作直线m,使它被两条已知直线l₁：x－3y+10=0和l₂：2x+y－8=0所截得线段以P为中点,求直线m的方程.

翰林汇

7、

求点P(3,5)关于直线l：x－3y+2=0对称的点的坐标.

翰林汇

8、

已知△ABC的一条内角平分线CD所在直线的方程是2x+y－1=0,两个顶点是A(1,2),B(－1,－1),求顶点C的坐标.

翰林汇

9、

已知一条动直线与两坐标轴相交,如果截距的倒数和为常数d(d≠0),求证这动直线必经过一定点,并求出这定点的坐标.

翰林汇

10、

光线从点A(3,－2)射到直线3x－2y＋3=0上一点N后被反射,反射光线经过点B(0,－4),求点N的坐标.

翰林汇

解析几何直线综合85（1） 〈答卷〉

一、选择题　　　　

1、　C  翰林汇

2、　A  翰林汇

3、　D  翰林汇

4、　C  翰林汇

5、　A  翰林汇

6、　D  翰林汇

7、　D  翰林汇

8、　C  翰林汇

9、　D  翰林汇

10、　C  翰林汇

11、　A  翰林汇

12、　B  翰林汇

13、　C  翰林汇

14、　D  翰林汇

15、　B  翰林汇

16、　B  翰林汇

17、　D  翰林汇

18、　A  翰林汇

19、　B  翰林汇

20、　C  翰林汇

21、　D  翰林汇

22、　D  翰林汇

23、　A  翰林汇

24、　D  翰林汇

25、　C  翰林汇

二、填空题　　　　

1、　

x－3y－6=0

翰林汇

2、　

4x＋3y－24=0,4x＋3y＋24=0

翰林汇

3、　

x－y+3－=0

翰林汇

4、　

2x＋y－4=0,x－2y－7=0

翰林汇

5、　

(3,3)或(－1,1)

翰林汇

6、　

(－

翰林汇

7、　

x－y＋1=0,x＋y－3=0

翰林汇

8、　

2x－y+4=0

翰林汇

9、　

a=12,b=－2,c=,d=－

翰林汇

10、　

(

翰林汇

三、计算题　　　　

1、　

略解： 如图, 设光线经l上点C反射.则∠1=∠2. 设A关于l对称的点为A^′, 则∠1=∠3, ∴∠2=∠3, 故B,C,A^′三点共线. 易得A^′的坐标A^′(10,-2), 则直线A^′B的方程为2x+y－18=0. 解方程组, 得点C的坐标, 则直线AC的方程为2x－11y+48=0　 ∴入射线所在直线方程为2x－11y+48=0, 反射线所在直线方程为2x+y－18=0.

　　　　　　　　 

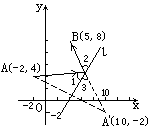
翰林汇

2、　

解：设点Q（a,b）, 则由PQ⊥l和PQ被l平分,有解得,  ∴点Q的坐标为.

翰林汇

3、　

解： (1) 由条件, 可设l^′的方程为 3x+4y+m=0, 以x=－1, y=3代入,

得 －3+12+m=0, 即得m=－9, ∴直线l^′的方程为 3x+4y－9=0;

(2) 由条件, 可设l^′的方程为4x－3y+n=0, 令y=0, 得, 令x=0, 得, 于是由三角形面积, 得n²=96, ∴

∴直线l^′的方程是 或

翰林汇

4、　

x+4y+4=0.

翰林汇

5、　

M(2,5) , 最大值为.

翰林汇

四、解答题　　　　

1、　

；2x－3y－6=0

翰林汇

2、　

P(2,0)　　Q(0,－4)

翰林汇

3、　

1

翰林汇

4、　

9x－33y＋8=0

翰林汇

5、　

(1)x－y－1=0；

(2)∠A=π－arctg3, ∠C=arctg, ∠B=arctg3－arctg

翰林汇

6、　

x+4y－4=0

翰林汇

7、　

(5,－1)

翰林汇

8、　

(－)

翰林汇

9、　

(,)

翰林汇

10、　

N(－)

翰林汇