金山区2005学年度第一学期期末高二数学试题
(满分：100分，完卷时间：90分钟)
| 题号 | 1~10 | 11~15 | 16 | 17 | 18 | 19 | 20 | 总分 |
|
|
|
|
|
|
|
|
|
|
一、填空题：(每小题4分，满分40分)
1、两条异面直线所成角的范围是 。
2、直线y=
x+1的倾斜角为 。
3、设集合M = {正方体}，N = {直四棱柱}，P = {正四棱柱}，Q = {直平行六面体}，则四个集合间的包含关系是 。
4、点A(3, –4)关于点M(–4, 3)的对称点B的坐标是 。
5、长方体共顶点的三条棱长分别是
、、
，则长方体的体对角线长为_____。
6、已知
=2
-
，
=-3+4，则
= 。
7、已知
={4, –3}，那么与同向的单位向量
=_______。
8、直线l过点(1, 3)，且与直线2x–3y+1=0平行，则直线l的方程为________。
9、直线l1：(a–2)x+(a+1)y+4=0与l2：(a+1)x+ay–9=0互相垂直，则a的值是 。
10、如果二面角a–l–b的平面角是锐角，空间一点P到平面α、β和棱l的距离分别为
和
，则二面角a–l–b的大小为
。
二、选择题：(每小题3分，满分15分)
11、在下列关于直线l、m与平面
、
的命题中，真命题是
( )
(A)若lÌb且a⊥b，则l⊥a (B)若l⊥b且a∥b，则l⊥a
(C)若l⊥b且a⊥b，则l∥a (D)若a∩b=m且l∥m，则l∥a
12、如果直线y=ax+2与直线y=3x–b关于直线y=x对称，那么a、b的值分别是 ( )
(A)
，6
(B)，–6 (C)3，–2
(D)3，6
13、a=3是直线ax+2y+3a=0和直线3x+(a–1)y=a–7平行且不重合的 ( )
(A)充分非必要条件 (B)必要非充分条件 (C)充要条件 (D)既非充分也非必要条件
14、设A，B，C，D是空间不共面的四点，且满足
，
，
，则△BCD是
( )
(A)钝角三角形 (B)直角三角形 (C)锐角三角形 (D)不确定
15、已知定点P(2,1)，分别在y=x及x轴上各取一点B与C，使
BPC的周长最小，则最小值为
( )
(A) 
(B) 2+ (C)3+
(D) 不存在
三、解答题：(共有5小题，满分45分，请写出必要的求解或证明过程)
16 、(满分8分)已知矩形ABCD的两个顶点分别是A(–1, 3)、B(–2,4)，若它的对角线的交点在x轴上，求另外两个顶点的坐标。
17、(满分8分) 若
与夹角为
，
，(1) 求的值；(2)试问
为何值时，
与
互相垂直。
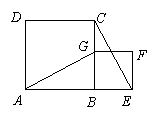18、(满分8分) 已知四边形ABCD、BEFG都是正方形，且A、B、E在同一条直线上，用坐标法证明：AG⊥CE。
19、(满分9分) 已知向量={1, 2}，
={x,1}，且
与
平行，(1) 求向量； (2) 已知点A(3 ,–1)，向量与垂直，求直线AB的一般式方程。
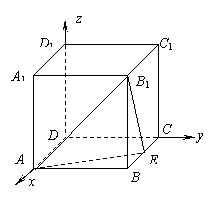20、(满分12分) 在正方体ABCD–A1B1C1D1中，E为棱BC的中点。(1) 在棱BB1上是否存在一点M，使D1M⊥平面B1AE？为什么？；(2) 在正方体表面ABB1A1上是否存在一点N，使D1N⊥平面B1AE？为什么？
金山区2005学年度第一学期期末高二数学试题评分标准
一、填空题(每小题4分，满分40分)
1、0o<q≤90o 2、60o 3、MÌPÌQÌN 4、(–11, 10) 5、
6、–10
7、{
, –
} 8、2x–3y+7=0
9、–1或1 10、15o 或75o
二、选择题(每小题3分，满分15分)
11、B 12、A 13、C 14、C 15、A
三、解答题
16、设C(x1, y1)、D(x2, y2)，由于AC、BD的交点在x轴上，即：AC、BD的中点在x轴上，
所以3+y1=0，4+y2=0，所以y1= –3，y2= –4，……………………………………3分
又AB⊥BC，所以kAB kBC= –1，kAB=–1，
所以kBC = 1，–3–4=x1+2，x1= –9，…………………………………………………5分
同理可得，x2= –8，…………………………………………………………………6分
所以C(–9, –3)、D(–8, –4)。…………………………………………………………8分
17、解：(1)由已知得：
，……………………3分
(2)又
…………………………………………5分
=27m–60+3(5m–9)=0…………………………………………………………7分
解得 
…………………………………………………………………8分
18、证明：分别以AB、AD所在的直线为x轴和y轴，如图建立直角坐标系。………2分
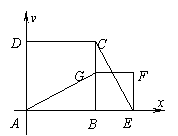设AB=a，BE=b，
则A(0,0)，G(a,b)，E(a+b,0)，C(a,a)…4分
kAG=
，kEC= –
，…………………………………6分
因为kAG.kEC= –1，所以AG⊥CE。………………8分
注意：本题如果用向量方法来证，相应给分。
19、解：(1) 因为：={1, 2}，={x,1}，
所以={1+2x, 4}，={2–x, 3}……………………………………………2分
又：∥，所以：
，即：
，故={
,1}…………4分
(2) 设B (x, y
)，则
；………………………………………………6分
由与垂直得：
。…………………………………………………………8分
所以直线AB的一般式方程为：x+2y–1=0……………………………………………9分
20、解：不妨设正方体的棱长为
，则
………………………………………2分
又：
……………………5分
假设BB1上存在一点
，使
平面B1AE成立，
则必有：AE；AB1
所以：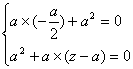
，此时方程组无解，…………………………………7分
故不存在点M，使平面B1AE。……………………………………………8分
(2) 假设正方体表面ABB1A1上存在一点
，使
平面B1AE成立。
则必有AE；AB1成立。由于
……………9分
所以：
解得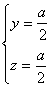
，……………………………………11分
即存在点
，也即正方体表面ABB1A1上存在一点N恰是正方形ABB1A1的中心，使平面B1AE成立。……………………………………………………12分