空间直线解答题
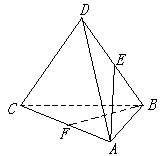
1、在空间四边形ABCD中,各边长和对角线长均为a,点E、F分别是BD、AC的中点,求异面直线AE和BF所成的角.
 翰林汇
翰林汇
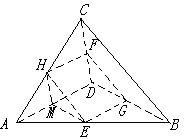
2、如图,空间四边形ABCD中,AB=AD=2,BC=DC=1,AD和BC成角60o,E、F分别是AB、DC的中点。求:
(1)AB和DC成角的度数;(2)EF的长。
 翰林汇
翰林汇
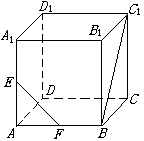
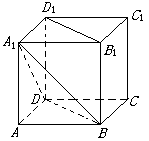
3、已知棱长为a的正方体ABCD—A1B
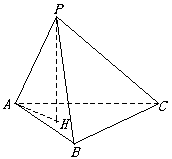
4、过锐角三角形ABC的垂心H作平面ABC的垂线,P为垂线上一点,![]() APB=90o,那么△BPC和△APC的形状如何?又若
APB=90o,那么△BPC和△APC的形状如何?又若![]() APB≠90o,PA与BC是否垂直?为什么?翰林汇
APB≠90o,PA与BC是否垂直?为什么?翰林汇
5、夹在两个平行平面![]() 和
和![]() 间的异面直线AB和CD所成的角为45o,它们在平面
间的异面直线AB和CD所成的角为45o,它们在平面![]() 内的射影长分别为
内的射影长分别为![]() 所成的角的差是45o.求异面直线AC和BD间的距离和它们所成角的度数.翰林汇
所成的角的差是45o.求异面直线AC和BD间的距离和它们所成角的度数.翰林汇
6、已知:矩形ABCD中,AB=45,直线EF//BC,交AB于E,交CD于F,且EB=28,将矩形AEFD沿直线EF折起,使AD和平面EBCF间的距离为15,求此时AD与BC间的距离.翰林汇
7、a、b是异面直线,它们所成角是60°.AB是a、b的公垂线,A![]() a,B
a,B![]() b,AB=1,另有C、D两点,C
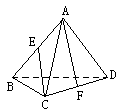
b,AB=1,另有C、D两点,C![]() a,D
a,D![]() b,且DB=AC=10,求C、D两点间距离.
b,且DB=AC=10,求C、D两点间距离.
翰林汇
8、平行四边形ABCD的内角C=60°,CD=2BC,沿对角线BD将平行四边形所在平面折成直二面角;求AC、BD所成的角.翰林汇
9、在边长a为的正方体ABCD-A1B
(1)异面直线AB与CC1间的距离为 ;
(2)异面直线A1D1与BC1所成角的度数为 ;
(3)若E,F分别为AA1,AB的中点,则异面直线EF与BC1所成角的大小
为 ;
(4)把两两都为异面直线的三条直线称为一组,在正方体ABCD-A1B
 翰林汇
翰林汇
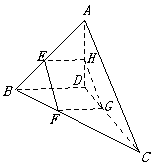
10、已知空间四边形ABCD.
(1)求证:对角线AC与BD是异面直线;
(2)若AC⊥BD,E,F,G,H分别这四条边AB,BC,CD,DA的中点,试判断四边形EFGH的形状;
(3)若AB=BC=CD=DA,作出异面直线AC与BD的公垂线段.翰林汇
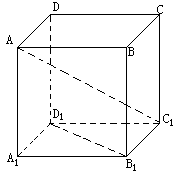
11、在正方体ABCD-A1B
12、在正方体ABCD-A1B
 翰林汇
翰林汇
13、已知AB,BC,CD为不在同一平面内的三条线段,AB,BC,CD的中点,P,Q,R满足PQ=2,![]() ,PR=3,求AC与BD所成的角。
,PR=3,求AC与BD所成的角。
翰林汇
14、在长方体ABCD-A1B
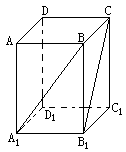 翰林汇
翰林汇
15、若E是正方体ABCD-A1B
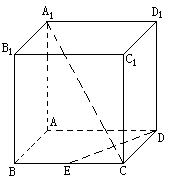 翰林汇
翰林汇
16、在长方体ABCD-A1B
 翰林汇
翰林汇
17、已知E,F,G,H顺次是空间四边形ABCD各边的中点。
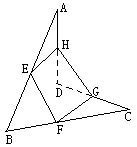
(1)求证:EFGH为平行四边形;
(2)如果AC=BD,那么EFGH是什么四边形?
(3)如果AC⊥BD,那么EFGH是什么四边形?
(4)如果AC=BD,且AC⊥BD,那么EFGH是什么四边形?
(5)若对角线BD=2,AC=4,求EG2+HF2的值。翰林汇
18、在正方体ABCD-A1B
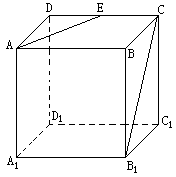 翰林汇
翰林汇
19、在空间四边形ABCD中,已知AD=1,![]() ,且AD⊥BC,对角线
,且AD⊥BC,对角线![]() ,
,![]() ,求AC和BD所成的角。翰林汇
,求AC和BD所成的角。翰林汇
20、在正四面体ABCD中,若E,F分别为棱AB,CD的中点,求AF与CE所成的角的正切值。
 翰林汇
翰林汇
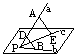
21、完成下列证明,已知直线a、b、c不共面,它们相交于点P,AÎa,DÎa,BÎb,EÎc求证:BD和AE是异面直线。
证明:假设__共面于g,则点A、E、B、D都在平面__内。
QAÎa,DÎa,∴__Ìγ.QPÎa,∴PÎ__.QPÎb,BÎb,PÎc,EÎc
∴__Ìg,__Ìg,这与____矛盾。∴BD、AE__________。
 翰林汇
翰林汇
22、在长方体ABCD-A′B′C′D ′中,已知AB=a,BC=b,AA′=c(a>b),求异面直线D′B与AC所成角的余弦值。
翰林汇
23、已知a、b为异面直线,A、B![]() a.AA1⊥b,BB1⊥b,A1、B1为垂足,若AB=2,A1B1=1,求异面直线a、b所成的角.翰林汇
a.AA1⊥b,BB1⊥b,A1、B1为垂足,若AB=2,A1B1=1,求异面直线a、b所成的角.翰林汇
24、已知异面直线a,b互相垂直,它们的公垂线段PQ=h,一条长为定值m(m>h)的线段AB两端分别在a,b 上滑动,求AB中点M的轨迹。翰林汇
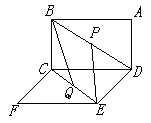
25、已知两个全等的正方形ABCD和CDEF所在平面互相垂直。
(1)求BD与EC所成的角;
(2)若P,Q分别为两个正方形的中心,求BQ与EP所成角的余弦值。
 翰林汇
翰林汇
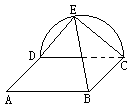
26、已知ABCD为矩形,E为半圆CED上一点,且平面ABCD⊥平面CDE.
(1)求证:DE是AD与BE的公垂线;
(2)若AD=DE=![]() ,求AD和BE所成角的大小。
,求AD和BE所成角的大小。
 翰林汇
翰林汇
27、完成下列证明:已知a∥b∥c,a∩d=A,b∩d=B,c∩d=C,求证:a、b、c、d共面。
证明:∵a//b,∴___确定一个平面a,∵AÎa,BÎb.
∴A__a,B__a,又∵AÎd,BÎd,∴___Ìa.同理dÌ(b、c确定的平面)b.
∵b、dÌ___,且b、dÌ__,bId=B,∴__与__重合,∴____共面。
说明:立几中证n条直线共面,一般可根据条件先确定一个平面(根据公理三及三推论),然后再证其它直线也在这个平面内;也可先确定n个平面,再证这些平面重合。翰林汇
28、在底半径为r的圆柱中,O、O′分别为上下底面圆的圆心,OM和O′N′分别为上下底面圆的两条半径,若异面直线OM和O′N′的成角为60o.求:异面直线MN′和OO′的距离。
空间直线解答题(参考答案)
1、 arccos![]() 翰林汇
翰林汇
2、 (1)60o;(2)![]() .翰林汇
.翰林汇
3、 提示:在面ABCD中作BP∥CE交DC的延长线于P,连D1P,在![]() BD1P中用余弦定理求得ÐD1BP=arccos
BD1P中用余弦定理求得ÐD1BP=arccos![]() .翰林汇
.翰林汇
4、 如图,H是垂心,PH是垂线,AH⊥BC,由三垂线定理得AP⊥BC,又AP⊥PB,故AP⊥平面PBC,从而AP⊥PC,△APC是直角三角形,同理△BPC也是直角三角形.由分析过程知PA⊥BC与否,与∠APB的大小无关,即PA⊥BC成立
 翰林汇
翰林汇
5、 90o,4或6.翰林汇
6、 25或39翰林汇
7、 提示:利用异面直线上两点间距离公式分类讨论:当∠DBE=60°时,CD=![]() .
.
当∠DBE=120°时,CD=![]() .翰林汇
.翰林汇
8、 如图,

折起前,∠A=∠C=60°,AD=BC=a,AB=DC=2a.
由余弦定理得BD2=a2+4a2-a·2a=3a2,∴BD=![]() .
.
∵AD2+BD2=AB2, ∴△ABD是直角三角形.
即∠ADB=90°.同理∠DBC=90°.折起后∠ADB=∠CBD=90°.
如图,
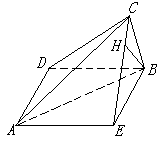
过A作AE![]() BD,连结AC、CE、BE,四边形AEBD是矩形,BD⊥BE,DB⊥BC.
BD,连结AC、CE、BE,四边形AEBD是矩形,BD⊥BE,DB⊥BC.
∴∠CBE是二面角A—BD—C的平面角.
∴∠CBE=90°,EC2=2a2.∵DB⊥平面EBC,∴DB⊥EC.
∵AE⊥EC,AC2=AE2+EC2=5a2,
由AE‖BD得∠CAE即为AC与BD所成的角.
在Rt△AEC中,cos∠CAE=![]() .
.
于是AC与BD所成角为arccos![]() .翰林汇
.翰林汇
9、 (1)a (2)45o (3)60o (4)8翰林汇
10、 (1)∵ABCD是空间四边形,
∴A点不在平面BCD上,而C![]() 平面BCD,∴AC过平面BCD外一点A与平面BCD内一点C,又∵BD
平面BCD,∴AC过平面BCD外一点A与平面BCD内一点C,又∵BD![]() 平面BCD,且C
平面BCD,且C![]() BD.∴AC与BD是异面直线.
BD.∴AC与BD是异面直线.
(2)解如图,∵E,F分别为AB,BC的中点,∴EF//AC,且EF=![]() AC.同理HG//AC,且HG=
AC.同理HG//AC,且HG=![]() AC.∴EF平行且相等HG,∴EFGH是平行四边形.又∵F,G分别为BC,CD的中点,∴FG//BD,∴∠EFG是异面直线AC与BD所成的角.∵AC⊥BD,∴∠EFG=90o.∴EFGH是矩形.
AC.∴EF平行且相等HG,∴EFGH是平行四边形.又∵F,G分别为BC,CD的中点,∴FG//BD,∴∠EFG是异面直线AC与BD所成的角.∵AC⊥BD,∴∠EFG=90o.∴EFGH是矩形.
(3)作法取BD中点E,AC中点F,连EF,则EF即为所求.
翰林汇
11、
解(1)如图,连结BD,A1D,∵ABCD-A1B1C1D1是正方体,∴DD1平行且相等BB1.∴DBB1D1为平行四边形,∴BD//B1D1.∴A1B,BD,A1D是全等的正方形的对角线.∴A1B=BD=A1D,△A1BD是正三角形,∴∠A1BD=60o,∵∠A1BD是锐角,∴∠A1BD是异面直线A1B与B1D1所成的角.∴A1B与B1D1成角为60o.
(2)连BD交AC于O,取DD1 中点E,连EO,EA,EC.
∵O为BD中点,∴OE//BD1.∵∠EDA=90o=∠EDC,ED=ED,AD=DC,∴△EDA≌△EDC,∴EA=EC.在等腰△EAC中,∵O是AC的中点,∴EO⊥AC,∴∠EOA=90o.
又∴∠EOA是异面直线AC与BD1所成角,∴AC与BD成角90o.
 翰林汇
翰林汇
12、 90°翰林汇
13、 90°翰林汇
14、 ![]() 翰林汇
翰林汇
15、 ![]() 翰林汇
翰林汇
16、 90°翰林汇
17、 (2)菱形;(3)矩形;(4)正方形;(5)10翰林汇
18、 ![]() 翰林汇
翰林汇
19、 90°翰林汇
20、 ![]() 翰林汇
翰林汇
21、 假设BD、AE共面于g,则点A、E、B、D都在平面g内。∵AÎa,DÎa,∴aÌg.∵PÎa,PÎg.∵PÎb,BÎb,PÎc,EÎc.∴bÌg,cÌg,这与a、b、c不共面矛盾。∴BD、AE是异面直线。
翰林汇
22、
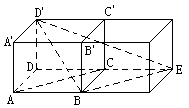
解:在长方体的一旁,补上一个全等的长方体,则BE≠AC,∠D′BE(或其补角)即D′B和CD所的角。
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() =
=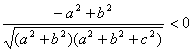
∴D′B与AC所成角的余弦值为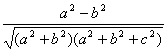 .翰林汇
.翰林汇
23、
解(如图)
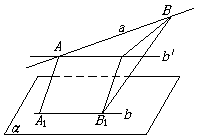
过A作直线b′‖b, 在b′上取一点C,使AC=A1B1,则AA1B1C为平行四边形,∵A1B1⊥AA1,∴AA1B1C为矩形,∴AC⊥B1C,又∵AC⊥A1B1,A1B1⊥BB1,∴AC⊥BB1,∴AC⊥平面BB1C,∴AC⊥BC.∴cos∠CAB=![]() ,∴∠CAB=60°,即a、b成60°角.翰林汇
,∴∠CAB=60°,即a、b成60°角.翰林汇
24、 M点的轨迹是以PQ为中点T为圆心、半径为![]() ,并位于PQ的垂直平分面上的圆。翰林汇
,并位于PQ的垂直平分面上的圆。翰林汇
25、 (1)60°;(2)![]() .翰林汇
.翰林汇
26、 (1)∵BC⊥面DEC,CE是BE在面DEC上的射影,而CE⊥DE,
∴BE⊥DE.又AD⊥面DEC,∴AD⊥DE,
故DE是AD与BE的公垂线;
(2)60°.
翰林汇
27、
∵a//b,∴a、b确定一个平面a,∵AÎa,BÎb.∴AÎa,BÎa.
又∵AÎd,BÎd,∴dÌa.同理dÌ(b、c确定的平面)b.
∵b、dÌa,且b、dÌb,b∩d=B,∴a与b重合,∴a、b、c、d共面。翰林汇
28、 d=![]() r翰林汇
r翰林汇