昆一中2005-2006学年度高二上学期期末数学试题
命题教师:杨洁民
注意:本试卷满分100分,考试时间为120分钟,请将全部试题做在答题卡上,只交答题卡。
一. 选择题(每小题3分,12小题,共36分)
1.抛物线![]() 的焦点坐标是( )
的焦点坐标是( )
A.(0,![]() )
B.(0,
)
B.(0,![]() ) C.(0,1) D.(0,2)
) C.(0,1) D.(0,2)
2.点0是空间的任意一点,A,B,C是不共线三点,若点P满足![]() 则当实数x,y,z满足下列哪个条件时P,A,B,C四点共面( )
则当实数x,y,z满足下列哪个条件时P,A,B,C四点共面( )
A. x=y=z B. x+y+z=-1 C. x+y+z=0 D. x+y+z=1
3.已知a,b为两条不同的直线,![]() ,
,![]() 为两个不同的平面,且a⊥
为两个不同的平面,且a⊥![]() ,b⊥
,b⊥![]() ,则下列命题中假命题是( )
,则下列命题中假命题是( )
A.若a∥b,则![]() ∥
∥![]() B.若
B.若![]() ⊥
⊥![]() ,则a⊥b
,则a⊥b
C.若![]() ,
,![]() 相交,则a,b相交
D.若a,b相交,则
相交,则a,b相交
D.若a,b相交,则![]() ,
,![]() 相交
相交
4.给出下列关于互不相同的直线m, l,n和平面![]() ,
,![]() 的四个命题:
的四个命题:
(1)若m![]()
![]() ,l∩
,l∩![]() =A,点A
=A,点A![]() m,则l与m不共面;
m,则l与m不共面;
(2)若m,l是异面直线,l∥![]() ,m∥
,m∥![]() 且n⊥l,n⊥m,则n⊥
且n⊥l,n⊥m,则n⊥![]() ;
;
(3)若l∥![]() ,m∥
,m∥![]() ,
,![]() ∥
∥![]() ,则l∥m;
,则l∥m;
(4)若l![]()
![]() , m
, m![]()
![]() ,l∩m=A, l∥
,l∩m=A, l∥![]() ,m∥
,m∥![]() ,则
,则![]() ∥
∥![]() ;
;
其中为假命题的是( )
A.(1) B.(2) C.(3) D.(4)
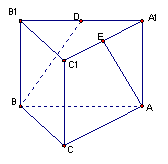 5.如图,在直棱柱
5.如图,在直棱柱![]() 中,∠AC=
中,∠AC=![]() ,D,E分别是
,D,E分别是![]() 和
和![]() 的中点,若AC=BC=
的中点,若AC=BC=![]() ,则BD和AE所成角的余弦值是( )
,则BD和AE所成角的余弦值是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.双曲线![]() 的两条渐近线互相垂直,那么该双曲线的离心率是( )
的两条渐近线互相垂直,那么该双曲线的离心率是( )
A.2 B.![]() C.
C.![]() D.
D.![]()
7.AB是异面直线a,b的公垂线段,AB=2,a,b成![]() 角,在a上取点P使AP=4,则点P到b的距离等于( )
角,在a上取点P使AP=4,则点P到b的距离等于( )
A.![]() 或
或![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
8.在一个二面角的一个面内有一点,它到棱的距离是它到另一个平面距离的二倍,那么这个二面角的度数是( )
A.![]() B.
B.![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
9.有下列命题:
(1)斜线a在平面![]() 上的射影为b,若直线c⊥b,则c⊥a;
上的射影为b,若直线c⊥b,则c⊥a;
(2)斜线a在平面![]() 上的射影为b,若直线c⊥b且c∥
上的射影为b,若直线c⊥b且c∥![]() ,则c⊥a;
,则c⊥a;
(3)设直线a,b在平面![]() 上的射影分别是
上的射影分别是![]() ,若
,若![]() ∥
∥![]() ,则a∥b;
,则a∥b;
其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
10.球面上有三点A,B,C组成球的内接三角形,若AB=9,BC=12,AC=15且球心到△ABC所在平面的距离为球半径的![]() ,则此球的体积是( )
,则此球的体积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.直线![]() 交抛物线
交抛物线![]() 于A,B两点,若AB的中点的横坐标为2,则AB等于( )
于A,B两点,若AB的中点的横坐标为2,则AB等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
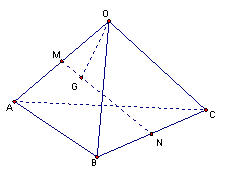 12.如图所示,空间四边形OABC,其对角线OB,AC,M,N分别为对边OA,BC的中点,点G在线段MN上,且分MN所成的比是1:2,现用基向量
12.如图所示,空间四边形OABC,其对角线OB,AC,M,N分别为对边OA,BC的中点,点G在线段MN上,且分MN所成的比是1:2,现用基向量![]() 表示的向量
表示的向量![]() ,设
,设![]() ,则x, y, z的值分别是( )
,则x, y, z的值分别是( )
A.![]()
B.![]()
C.![]()
D.![]()
二.填空题:(每小题4分,4小题,共16分)
13.圆心为(2,1)且被直线x-y-1=0截得的线段长为![]() 的圆的方程____________________;
的圆的方程____________________;
14.在空间内有两条成![]() 角的直线,过空间的一点P与这两条直线都成
角的直线,过空间的一点P与这两条直线都成![]() 角的直线有_________条;
角的直线有_________条;
15.已知直线![]() :2x-y-1=0,
:2x-y-1=0,![]() :3x+y-2=0,则
:3x+y-2=0,则![]() 到
到![]() 的角为________________;
的角为________________;
16.正三棱锥的一个侧面与底面面积之比为2:3,则这个三棱锥的侧面与底面所成二面角的大小为__________________________;
三.解答题(本大题共5小题,满分48分)
17.(本小题8分)已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设![]()
(1)求![]() 和
和![]() 的夹角
的夹角![]() 的余弦值;
的余弦值;
(2)若向量![]() 与
与![]() 互相垂直,求k的值.
互相垂直,求k的值.
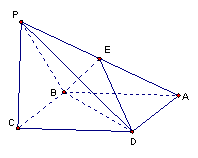
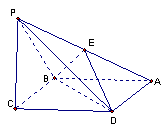
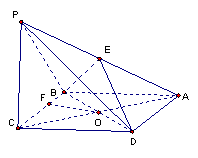
18.(本小题10分)如图,ABCD是边长为a的菱形,∠BAD=![]() ,PC⊥平面ABCD,PC=a,E是PA的中点
,PC⊥平面ABCD,PC=a,E是PA的中点
(1)求证:平面BDE⊥平面ABCD;
(2)求点E到平面PBC的距离.
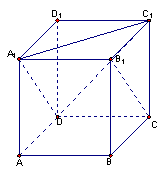
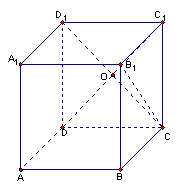
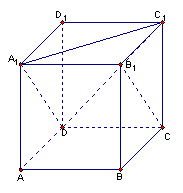 19.(本小题10分)如图,正方体
19.(本小题10分)如图,正方体![]() 中,
中,![]() 的棱长为1,
的棱长为1,
(1)求直线BC与直线![]() 的距离;
的距离;
(2)求直线![]() 与平面
与平面![]() 的距离.
的距离.
20.(本小题10分)已知直线l过点A(-3,2),且与抛物线![]() 只有一个公共点,求直线l的方程;
只有一个公共点,求直线l的方程;
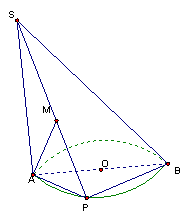
21.(本小题10分)AB为圆O的直径, 圆O在平面![]() 内,SA⊥
内,SA⊥![]() ,P在圆周上移动(异于A,B),M为A在SP上的射影
,P在圆周上移动(异于A,B),M为A在SP上的射影
(1)求证:三棱锥S-ABP的各面均是直角三角形;
(2)求证:AM⊥面SPB

 昆一中2005-2006学年度高二年级上学期期末考试
昆一中2005-2006学年度高二年级上学期期末考试
高二数学答题卷
一. 选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二.填空题:
13._____________________________; 14._________________________________;
15._____________________________; 16._________________________________;
三.解答题:
17.
18.
 19.
19.
20.
 21.
21.
高二(上)数学试卷参考答案
一. 选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | C | C | A | B | D | C | B | A | C | D |
二.填空题:
13.![]() 14.
4条 15.
14.
4条 15.![]() 16.
16.![]()
三.解答题:
17.解:据题意得:![]()
(1)cos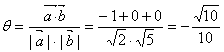
∴![]() 与
与![]() 夹角
夹角![]() 的余弦值是
的余弦值是![]()
(2)![]() =(k-1,k,2)
=(k-1,k,2)
![]() =(k+2,k,-4)
=(k+2,k,-4)
∵![]() ⊥
⊥![]()
 ∴(k-1,k,2).(k+2,k,-4)=(k-1)(k+2)+
∴(k-1,k,2).(k+2,k,-4)=(k-1)(k+2)+![]() -8=0
-8=0
∴![]() +k-10=0
∴
+k-10=0
∴![]() 或k=2
或k=2
18.(1)证明:如图,设O是对角线AC,BD的交点
∵E是PA的中点 ∴EO∥PC
由已知PC⊥平面ABCD,得EO⊥平面ABCD
又∵EO![]() 平面BDE
平面BDE
∴平面BDE⊥平面ABCD
(2)解:∵EO∥PC, ∴EO∥平面PBC
∴E到平面PBC的距离等于O到平面PBC的距离
作OF⊥BC于F,又OF⊥PC
∴OF⊥平面PBC
由已知△BDC为正三角形
高h=![]()
∴OF等于高的一半,即OF=![]()
∴E到平面PBC的距离为![]()
19.解: (1)如图,连结![]() 交
交![]() 于O,则CO⊥
于O,则CO⊥![]()
 又∵BC⊥面
又∵BC⊥面![]() ∴ BC⊥CO
∴ BC⊥CO
∴线段CO为直线![]() 的公垂线段
的公垂线段
∴所求距离为![]()
(2)如图可证平面![]() ∥平面
∥平面![]()
∴直线![]() 与平面
与平面![]() 的距离就转化成平面
的距离就转化成平面![]() 与平面
与平面![]() 的距离
的距离
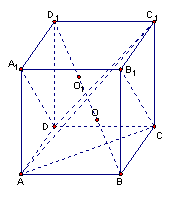 连接
连接![]() 可证
可证![]() ⊥平面
⊥平面![]()
设垂足为O,那么![]() ⊥平面
⊥平面![]() 设垂足为
设垂足为![]()
∴![]() 的长为所求
的长为所求
正三棱锥![]() 的体积
的体积
=![]()
∴BO=![]() 同理可得
同理可得![]()
∴![]()
20.解:设直线l的斜率为k,则l:y-2=k(x+3)
![]() 由 y-2=k(x+3)
由 y-2=k(x+3)
![]() 得
得![]()
当k=0时 ,方程y=2有唯一解
当k≠0时,令△=0得k=-1或k=![]() 此时方程有两个相同的实数根
此时方程有两个相同的实数根
∴直线方程为y=2 x+y+1=0 与x-3y+9=0
21.证明: (1)∵SA⊥面![]() AP
AP![]()
![]() AB
AB![]()
![]() ∴SA⊥AP SA⊥AB
∴SA⊥AP SA⊥AB
∴△SAP,△SAB为直角三角形
又∵AB是直径 ∴PB⊥AP SA⊥面![]()
∴SA⊥PB ∵AP∩SA=A ∴PB⊥面SAP
∵SP![]() 面SAP ∴PB⊥SP
面SAP ∴PB⊥SP
∴△SPB是直角三角形, △APB也是直角三角形
(2)∵SA⊥面APB ,PB![]() 面APB
面APB
∴SA⊥PB 又PB⊥AP
 ∴PB⊥面SAP ∵AM
∴PB⊥面SAP ∵AM![]() 面SAP
面SAP
∴PB⊥AM 又∵AM⊥SP PB∩SP=P
∴AM⊥面SPB
