含有绝对值的不等式
A卷
一、选择题
1、设命题A：2＜x＜3，命题B： x－2 ＜1，那么( )
A、A是B的充分不必要条件 B、A是B的必要不充分条件
C、A是B的必要条件 D、A是B的既不充分也不必要条件
2、下列不等式有实数解的是( )
A、x2 + (x－1)2≤0 B、
C、 x2－x + 1≤x2－x + 1 D、 x－5 + 2－x＜3
3、不等式1≤ x－2 ≤7的解集是( )
A、{x x ≤1或x≥3} B、{x 1≤x ≤3}
C、{x －5≤x ≤1或3≤x ≤9} D、{x－5≤x ≤9}
4、若a，b，c
，且 a－c ≤ b ，则( )
A、 a ≥ b + c B、 a ≤ b － c
C 、 a ≤ b + c D、 a ≥ c － b
5、不等式 x－1 + x + 2 ＜5的解集是( )
A、{ x －3＜x＜2}
B、{ x －1＜x＜2} C、{ x －2＜x＜1} D、
6、已知四个实数a、b、c、d满足a + d = b + c且 a－d ＜ b－c ，则有( )
A、a d = b c B、a d ＜ b c C、a d ＞ b c D、a d与b c的关系不确
7、若A = 
( )
A、{ 1 } B、{ 0，1} C、(0，1} D、[0，1]
8、 x－A
的( )
A、充分而非必要条件 B、必要而非充分条件 C、充分且必要条件 D、以上都不是
9、设xy＜0，x，y
，那么正确的是( )
A、 x + y ＞ x－y B、 x－y ＜ x + y
C、 x + y ＜ x－y D、 x－y ＜ x － y
二、填空题
10、不等式 x + 1＜1的解集是 。
11、不等式x2 + x －6＜0的解集是 。
12、能使不等式
成立的整数集合是
。
13、若a，b，且 a ≤3， b ≤2，则 a + b的最大值是
，最小值是 。
14、不等式 x2－4≤x + 2的解集是 。
15、对一切实数x，不等式 x－3 + x + 2 ＞a恒成立，则a的取值范围是 。
三、解答题
16、已知x≠0，求证：
。
17、已知f(x) = x2－x + 13,且 x－a＜1，求证：f(x)－f(a) ＜2( a + 1)。
18、解不等式
。
19、国家为了加强对烟酒生产管理，实行征收附加税政策，现知某种酒每瓶70元，不征收附加税时，每年大约产销100万瓶，若政府征收税，每销售100元征税R元(叫做税率R%)，则每年产销量将减少10R万瓶，要使每年在此项经营中所收附加税不少于112万元，R应怎样确定？
B卷
一、综合题
1、已知 a ＜1， b ＜1，求证：
。
2、已知a，b
R，求证：
。
3、解不等式 x + 3 － 2x + 1 ＜
。
二、应用题
4、已知某轮船速度为每小时10km时，燃料费用为每小时30元，其余费用为每小时480元，设轮船的燃料费用与其速度的立方成正比，问轮船航行的速度为每小时多少千米时，每千米航行费用总和最小。
三、创新题
5、设f(x) = ax2 + bx + c(a≠0),当 x ≤1时,总有 f(x) ≤1,求证 f(2) ≤8。
6、已知a，bR，求证：
。
四、高考题
7、对于任意的实数x，不等式 x + 1 ≥kx恒成立，则实数k的取值范围是( )
A、(－∞，0) B、[－1，0] C、[0，1] D、[0，+∞)
8、不等式(1 + x )(1－ x )＞0的解集是( )
A、{ x 0≤x＜1} B、{x x＜0且x≠－1}
C、{x －1＜x＜1} D、{ x x＜1且x≠－1}
参考答案
一、选择题
1、A 2、C 3、C 4、C 5、A 6、C 7、A 8、A 9、C
二、填空题
10、－2＜x＜0 11、{x －2＜x＜2} 12、{－2，0} 13、5，0
14、{x 1≤x≤3或x = －2} 15、a＜5
三、解答题
16、证明：由于有
有x与
的符号相同
：
即
17、证明：∵
18、
19、{
B卷
一、综合题
1、要证
即
又∵
2、证明：当a + b = 0时，不等式显然成立；
当a + b≠0时，∵
于是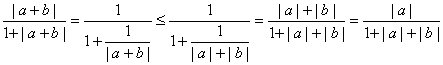
+
∴
3、
二、应用题
4、
三、创新题
5、证明：由已知
①又∵
∴
②∵
∴
③
由①②③知
6、证明：
=
∴当
∴原不等式成立
四、高考题
7、C 8、D