衡阳市田家炳实验中2005年高二上期末模拟考试
班级_______ 姓名__________ 学号______
一、选择题(本大题共10小题,每小题5分,共50分)
1.设全集I=R,集合P={x2x2-x<0},集合Q={x![]() ≤2},则 ( )
≤2},则 ( )
A.P![]() RQ B.P=
RQ B.P=![]() RQ
RQ
C.P∪Q=R D.P∪Q={xx>0}
2.当x∈[-1,3]时,不等式a≥x2-2x-1恒成立,则a的最大值和最小值分别为( )
A.2,-1 B.不存在,2
C.2,不存在 D.-2,不存在
3.如果实数x、y满足(x-2)2+y2=3,那么![]() 的最大值是 ( )
的最大值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.当-1≤x≤1时,y=ax+2a+1的值有正也有负,则实数a的取值范围是( )
A.a<0或a>1 B.0<a≤1
C.-1<a<-![]() D.a≤-1或a≥-
D.a≤-1或a≥-![]()
5. 已知两定点F1(-1,0) 、F2(1,0), 且![]() 是
是![]() 与
与![]() 的等差中项,则动点P的轨迹是( ).
的等差中项,则动点P的轨迹是( ).
A. 椭圆 B. 双曲线 C. 抛物线 D. 线段
6、已知平面内动点M(x,y)到定点A(6,0)的距离与到直线x=3的距离之比为![]() ,则M的轨迹是( )。
,则M的轨迹是( )。
A 抛物线; B 椭圆 ; C 双曲线 ; D 圆。
7. 设![]() ,“
,“![]() ”是“曲线
”是“曲线![]() 为椭圆”的 ( )
为椭圆”的 ( )
A.必要非充分条件 B.充分非必要条件
C.充分必要条件 D.既非充分又非必要条件
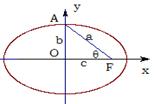 8. 如图,已知
8. 如图,已知![]() 是椭圆
是椭圆![]() 的半焦距,则
的半焦距,则![]() 的 取值( )
的 取值( )
A (1, +∞) B ![]()
C ![]() D
D ![]()
9.过原点的直线l与双曲线![]() -
-![]() =-1有两个交点,则直线l的斜率的取值范围是 ( )
=-1有两个交点,则直线l的斜率的取值范围是 ( )
A.(-![]() ,
,![]() )
B.(-∞,-
)
B.(-∞,-![]() )∪(
)∪(![]() ,+∞)
,+∞)
C.[-![]() ,
,![]() ]
D.(-∞,-
]
D.(-∞,-![]() ]∪[
]∪[![]() ,+∞)
,+∞)
10、已知曲线bx2+ay2=ab与直线ax+by+1=0(a,b为非零实数),在同一坐标系中,它们的图形可能是( )
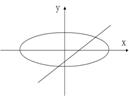
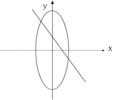
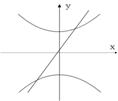

A B C D
二、填空题(本大题共5小题,每小题4分,共20分)
11. 已知椭圆![]() 的一条准线方程是x=
的一条准线方程是x=![]() ,则b=
。翰林汇
,则b=
。翰林汇
12.已知-![]() <α<
<α<![]() ,-π<β<
,-π<β<![]() ,则2α-
,则2α-![]() β的取值范围是_________.
β的取值范围是_________.
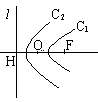 13.配制A、B两种药剂,需要甲、乙两种原料,已知配一剂A种药需甲料3 mg,乙料5 mg;配一剂B种药需甲料5 mg,乙料4 mg.今有甲料20 mg,乙料25 mg,若A、B两种药至少各配一剂,应满足的条件是__________.
13.配制A、B两种药剂,需要甲、乙两种原料,已知配一剂A种药需甲料3 mg,乙料5 mg;配一剂B种药需甲料5 mg,乙料4 mg.今有甲料20 mg,乙料25 mg,若A、B两种药至少各配一剂,应满足的条件是__________.
14. 如图, 直线l ^ FH于H, O为FH的中点, 曲线C1 ,
C2是以F为焦点, l为准线的圆锥曲线(图中只画出曲
线的一部分), 那么圆锥曲线C1是 ;
圆锥曲线C2是 .
15.抛物线y2=4x的弦AB垂直于x轴,若AB的长为4![]() ,则焦点到AB的距离为 ;
,则焦点到AB的距离为 ;
三、解答题(本大题共6小题,共80分)
16.( 12分) 在R上定义运算![]() ,若不等式
,若不等式![]() 对任意实数
对任意实数![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
17.已知a,b>0,a+b=1.求证:(1+![]() )(1+
)(1+![]() )≥9.(12分)
)≥9.(12分)
18.( 14分)已知圆C:(x-1)2+(y-2)2=25及直线l:(2m+1)x+(m+1)y=7m+4 (m∈R).
(1)证明不论m取什么实数,直线l与圆C恒相交;
(2)求直线l被圆C截得的弦长的最短长度及此时的直线方程.
19.(14分) 已知椭圆![]() =1(a>b>0)的离心率
=1(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.
(1)求椭圆的方程;(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
20.( 14分)如图,某农场在P处有一堆肥,今要把这堆肥料沿道路PA或PB送到庄稼地ABCD中去,已知PA=100 m,PB=
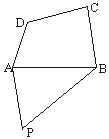
21.(14分) 在平面直角坐标系xOy中,抛物线y=4x2上异于坐标原点O的两不同动点A、B满足AO⊥BO, 如图所示.
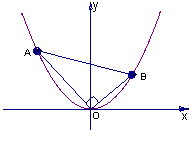 (Ⅰ)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅰ)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)△AOB的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
参考答案
一.选择题
1.A 2. B 3. D 4. C 5. A 6. C 7. A 8. C 9. B 10. D
二.填空题:
11,5 12,(-![]() ,
,![]() ) 13, 14,椭圆 ; 双曲线 15,2。
) 13, 14,椭圆 ; 双曲线 15,2。
三、解答题(本大题共6小题,共80分)
16. 1<x<4 ;
17.证明:![]() =
=![]()
=![]()
![]() (1+
(1+![]() )(1+
)(1+![]() )≥9.
)≥9.
18(1)证明:若按常规思路只需圆心O(1,2)到直线l的距离恒小于半径即可,但注意到直线l的方程写成x+y-4+m(2x+y-7)=0后,发现直线l过直线x+y-4=0与直线2x+y-7=0的交点(3,1).若该定点在圆内部,则问题(1)得证.
∵(3-1)2+(1-2)2=5<25,
∴点(3,1)在圆内部.
∴不论m为何实数,直线l与圆恒相交.
(2)解:从(1)的结论知直线l过定点M(3,1)且与过此点的圆O的半径垂直时,l被圆所截的弦长AB最短,由垂径定理知
AB=2![]()
=2![]() =4
=4![]() .
.
此时kl=-![]() ,即-
,即-![]() =-
=-![]() =2,
=2,
解得m=-![]() ,代入,得直线l方程为2x-y-5=0.
,代入,得直线l方程为2x-y-5=0.
19.(14分) 解析:(1)直线AB方程为:bx-ay-ab=0. …1分
依题意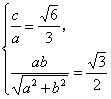 解得
解得  …5分
…5分
∴ 椭圆方程为 ![]() .
…6分
.
…6分
(2)假若存在这样的k值,由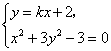
得![]()
![]() .
…7分
.
…7分
∴ ![]() . ①
…8分
. ①
…8分
设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则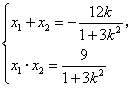 ②
…9分
②
…9分
而![]() .
…10分
.
…10分
要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE,即![]() 时,
时,
有![]() .
…11分
.
…11分
∴ ![]() . ③
…12分
. ③
…12分
将②式代入③整理解得![]() .经验证,
.经验证,![]() ,使①成立.
…13分
,使①成立.
…13分
综上可知,存在![]() ,使得以CD为直径的圆过点E .
…14分
,使得以CD为直径的圆过点E .
…14分
20.解:设M是这种界线上的点,
则必有MA+PA=MB+PB,
即MA-MB=PB-PA=50.
∴这种界线是以A、B为焦点的双曲线靠近B点的一支.建立以AB为x轴,AB中点 O为原点的直角坐标系,则曲线为![]() -
-![]() =1,
=1,
其中a=25,c=![]() AB.
AB.
∴c=25![]() ,b2=c2-a2=3750.
,b2=c2-a2=3750.
∴所求曲线方程为![]() -
-![]() =1(x≥25,y≥0).
=1(x≥25,y≥0).
21.(14分)解:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),
则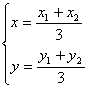 …(1)…… 2分
…(1)…… 2分
∵OA⊥OB ∴![]() ,即
,即![]() ,……(2) …… 4分
,……(2) …… 4分
又点A,B在抛物线上,有![]() ,代入(2)化简得
,代入(2)化简得![]() …… 5分
…… 5分
∴![]()
所以重心为G的轨迹方程为![]() …… 7分
…… 7分
(II)![]()
![]() …… 9分
…… 9分
由(I)得![]() …… 11分
…… 11分
![]() …… 12分
…… 12分
当且仅当![]() 时,等号成立
时,等号成立![]() …… 13分
…… 13分
所以△AOB的面积存在最小值,且最小值为1 . …… 14分