湖北省黄冈中学2005年秋季高二数学期末考试试题（文科）

命题人：曾建民　　 校对人：陈晓洁

一、选择题：本大题共12个小题，每小题5分，共60分.在每小题所给出的四个选项中，只有一项是符合题目要求的.

1．已知a, b∈R，若a+b=1，则下列各式中成立的是（　　）

　 A．a+b>1　　 　　　　　　　　　　　　　　　　 　　B．a+b≥1　　　

 C．a+b<1　　　　　　　 　　　　　　　　　　　　　　　D．a+b≤1

2．下列命题中，正确的是（　　）

　 A．经过不同的三点有且只有一个平面

　 B．平行于同一平面的两条直线互相平行

　 C．分别和两条异面直线都相交的两条直线是异面直线

　 D．若一个角的两边和另一个角的两边分别平行，则这两个角相等或互补

3．抛物线y=4x²的准线方程是（　　）

　 A．x=1　　　　　　　　　 　 B．　　　　　　　 C．y=－1　　　　　 D．

4．已知圆C与圆关于直线y=x对称，则圆C的方程是（　　）

　 A．　　　　　　　　　　　　　　　　　　 B．

　 C．　　　　　　　　　　　　　　　　　　　　 　 D．

5．不等式的解集为（　　）

　 A．　　　　　　　　　　　　　　　　　　　　　　　　　 B．（0，1）　　 　

 C．　　　　 　　　　　　　　　　　　　　 D．

6．若P为双曲线的右支上一点，且P到右焦点的距离为4，则P到左准线的距离为（　　）

　 A．3　　　　　　　　　　　　 B．6　 　　　　　　　　　 　C．　　　　　　　　　　 　 D．10

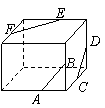7．如图，A、B、C、D、E、F分别为正方体相应棱的中点，对于直线AB、CD、EF，下列结论正确的是（　　）

　 A．AB∥CD　　　　　　　　　　　　 　 B．CD与EF异面　　

 C．AB与CD相交　　　　　　　　　 D．AB与EF异面

8．已知，当取最小值时，的值为（　　）

　 A．0°　　　　　　　　　B．90°　　　　　　　　　 　 C．180°　　　　　　　 　 D．60°

9．设为不重合的平面，为不重合的直线，给出下列四个命题：

①；　　  ②若；

③若； ④若.

其中是真命题的个数是（　　）

　 A．1　　　　　　　 　　　B．2　　　　　　　　　　 　 C．3　　　　　　　 　　　D．4

10．已知实数x, y满足，则的最小值是（　　）

　 A．　　　　　　　　　　　 B．　　　　　　　　 　 C．　　　　　　　　　　 D．2

11．若双曲线与直线无交点，则离心率的取值范围是

（　　）

　 A．　　　　　　 　 B．　　　　　　 　 C．　　　　　　　　　 D．

12．E、F是椭圆的左、右焦点，是椭圆的一条准线，点P在上，则∠EPF的最大值是（　　）

　 A．60°　　　　　　 B．30°　 　　C．90° 　　　 D．45°

选择题答题卡

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：本大题共4小题，每小题4分，共16分.把答案写在横线上.

13．若为圆的弦AB的中点, 则直线AB的方程为____________.

14．过抛物线的焦点作直线交抛物线于A(x₁, y₁), B(x₂, y₂)两点，则y₁y₂=_______.

15．已知关于x的不等式的解集为M，若，则a的取值范围是________________.

16．某单位需购液化气106千克，现在市场上该液化气有两种瓶装，一种是瓶装35千克，价格为140元；另一种是瓶装24千克，价格为120元. 在满足需要的情况下，最少要花费_________________元.

三、解答题：本大题共6个小题，共74分.解答应写出文字说明、证明或演算步骤.

17．（本小题满分12分）求经过点A（3，2），圆心在直线y=2x上，且与直线y=2x+5相切的圆的方程.

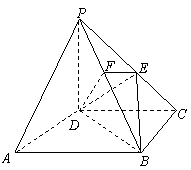18．（本小题满分12分）如图，ABCD为正方形，PD⊥平面AC，PD=DC，E是PC的中点，作EF⊥PB交PB于点F.

（1）证明：PA∥平面EDB；

（2）证明：PB⊥平面EFD.

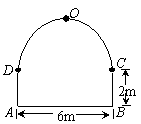
19．（本小题满分12分）一座拱桥桥洞的截面边界由抛物线弧段COD和矩形ABCD的三边组成，拱的顶部O距离水面5m，水面上的矩形的高度为2m，水面宽6m，如图所示.一艘船运载一个长方体形的集装箱，此箱平放在船上，已知船宽5m，船面距离水面1.5m，集装箱的尺寸为长×宽×高=4×3×3(m). 试问此船能否通过此桥？并说明理由.

20．（本小题满分12分）如图，在长方体ABCD—A₁B₁C₁D₁，AB=BC=1，AA₁=2，E为CC₁的中点，F为BD₁的中点.

（1）求异面直线D₁E与DF所成角的大小；

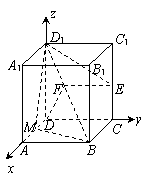（2）M为直线DA上动点，若EF⊥平面BMD₁，则点M在直线DA上的位置应是何处？

 

21．（本小题满分12分）已知双曲线的右焦点为F，过点F作直线PF垂直于该双曲线的一条渐近线于.

（1）求该双曲线方程；

（2）设A、B为双曲线上两点，若点N（1，2）是线段AB的中点，求直线AB的方程.

22．（本小题满分14分）如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，M为CD的中点.

（1）求点M的轨迹方程；

（2）过M作AB的垂线，垂足为N，若存在正常数，使，且P点到A、B 的距离和为定值，求点P的轨迹E的方程；

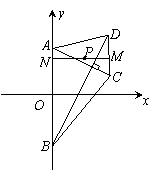（3）过的直线与轨迹E交于P、Q两点，且，求此直线方程.

2005年秋高二数学参考答案（文）

1.B  2.D　3.D　4.A  5.D　6.C　7.D  8.B　9.B　10.A　11.A　12.B

13．x－y－3=0　　　　　　 14．－4　　　　 15．[2, 3]∪[9, +∞)　　　　　　16．500

17．解：设圆心坐标为（a, 2a），则.

∴5a²－14a+8=0.　∴a=2或.　 故所求圆的方程为

18．（1）连结AC，设AC∩BD=0，连结EO，∵底面是正方形，∴O为AC的中点

∴OE为△PAC的中位线　 ∴PA∥OE，而OE平面EDB，PA平面EBD，∴PA∥平面EDB.

（2）∵PD⊥平面AC，BC平面AC，∴BC⊥PD，而BC⊥CD，PD∩CD=D.

∴BC⊥平面PDC.　∵DE平面PDC　, ∴BC⊥DE .　①

又∵PD⊥平面AC，DC平面AC，　∴PD⊥DC，而PD=DC，

∴△PDC为等腰三角形 .　∴DE⊥PC .　 ②　　

由①、②可知DE⊥平面PBC， ∴DE⊥PB.又EF⊥PB,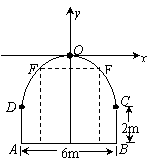 ∴PB⊥平面DEF.

（可建立空间直角坐标系证明。略）

19．解：建立如图所示的平面直角坐标系，使抛物线顶点O在坐标原点，对称轴与y轴重合，设抛物线方程为x²=ay (a<0)

由题设条件知C（3，－3）在抛物线上，

∴9=－3a， a=－3，即抛物线方程为x²=－3y.

要使船能顺利通过，应有集装箱最高处E、F关于y轴对称.

于是设F（1.5, y₀），则1.5²=－3y_0.

∴y₀=－0.75　 此时点F距离水面的高度为5－0.75=4.25.

而集装箱高加船高为3+1.5=4.5>4.25，故此船不能通过此桥.

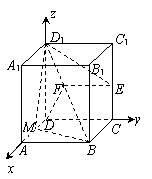20．（1）以D为坐标原点建立如图所示的空间直角坐标系，则D（0，0，0），B（1，1，0），D₁（0，0，2），E（0，1，1），F（，，1）.　 ∴.

则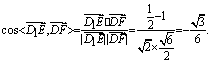

故异而直线D₁E与DF所成角为.

（2）设点M（x, 0, 0），则

由EF⊥平面BMD₁，有　 可得x=0.∴点M的坐标为M(0,0,0).

故当EF⊥平面BMD₁时，M在直线DA上的D点处.

（也可不建立空间直角坐标系求解。略）

21．解：(1)设半焦距为C，则F（C，0），直线l₁的方程为，直线PF的方程为

解方程组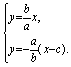　可得，又已知P点坐标为

∴　∴双曲线方程为

① ②

（2）设A(x₁, y₁), B(x₂, y₂)，则有

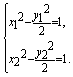
　　②－①, 得.　∴

即直线AB的方程为, 即

22．解：（1）设点M的坐标为M(x, y)(x≠0)，则

又 由AC⊥BD有，即，∴x²+y²=1（x≠0）.

（2）设P（x, y），则，代入M的轨迹方程有

即，∴P的轨迹方程为椭圆（除去长轴的两个端点）.

要P到A、B的距离之和为定值，则以A、B为焦点，故.

∴　从而所求P的轨迹方程为9x²+y²=1(x≠0).

（3）易知l的斜率存在，设方程为

联立9x²+y²=1，有

设P(x₁, y₁), Q(x₂, y₂)，则.

∵，而

∴.　　整理，得　 ∴

即所求l的方程为