湖北随州曾都一中05—06学年高二上学期期末调研
数 学 试 题（文理合卷）（元月11日15：00---17：00）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分． 时间120分钟，分数150分
第Ⅰ卷（选择题，共60分）
一、选择题（本大题共有12个小题，每小题5分；在每小题给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在试卷指定的位置上。）
1．坛子里放有2个白球，3个黑球，从中进行不放回摸球． A1表示第一次摸得白球，A2表示第二次摸得白球，则A1与A2是
A．互斥事件 B．独立事件 C．对立事件 D．不独立事件
2．
的展开式中，
的系数为
A．－40 B．
3．若直线
到直线
的角为
，则实数
的值等于
A．0 B．
C．0或 D．
4. 若椭圆
的离心率是
，则双曲线
的离心率是
A．
B．
C．
D．
5．湖北省分别与湖南、安徽、陕西三省交界,且湘、皖、陕互不交界，在地图上分别给各省地域涂色，要求相邻省涂不同色，现有五种不同颜色可供选用，则不同的涂色方法的种数是
A．240 B．
6.椭圆
的焦点在
轴上，长轴长是短轴长的两倍，则
的值为
A．
B．
C． 2 D．4
7．任意写一个无重复数字的三位数，其中十位上的数字最小的概率是
A．
B．
C．
D．
8．设(3x
+x
)
展开式的各项系数之和为t，其二项式系数之和为h，若t+h=272，则展开式的x
项的系数是
A．
B．
9、若不论
为何值，直线
与曲线
总有公共点，则
的取值范围是
A.
B.
C.
D.
10．若双曲线
的渐近线l方程为
，则双曲线焦点F到渐近线l的距离为
A．2 B．
C．
D．2
11.（文科）设离心率为
的双曲线
（
，
）的右焦点为
，直线
过点且斜率为
，则直线与双曲线
的左、右两支都相交的充要条件是
A．
B． 
C．
D．
（理科）已知定点M（1，
给出下列曲线方程：
① 4x+2y-1=0 ②
③
④
在曲线上存在点P满足
的所有曲线方程是
A.①③ B.②④ C.①②③ D.②③④
12、（文科）椭圆
上一点M到焦点
的距离为2，
是
的中点，则
等于
A．2 B．
C．
D．
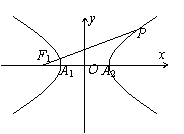（理科）如图，双曲线＝1的左焦点为F1，顶点为A1，A2，P是双曲线上任意一点，则分别以线段PF1、A
A.相交 B.相切 C.相离 D.以上情况都有可能
二、填空题（本大题共4小题，每小题4分，共16分）
13. 椭圆的焦点为F1、F2，过点F1作直线与椭圆相交，被椭圆截得的最短的线段MN长为
，
的周长为20，则椭圆的离心率为 __________
14.若焦点在
轴上的椭圆
上有一点，使它与两焦点的连线互相垂直，则正数的取值范围是_______________
15．点
到直线
的距离等于4，且在不等式
表示的平面区域内，则点
的坐标是_______________.
16．三位数中、如果十位上的数字比百位上的数字和个位上的数字都小，则这个数为凹数，如524、746等都是凹数。那么各个数位上无重复数字的三位凹数共有_____个．
三、解答题(本大题6小题, 解答应写出文字说明、证明过程或演算步骤)
17．一个口袋中装有大小相同的2个白球和3个黑球。
（1）从中摸出两个球，求两球恰好颜色不同的概率；
（2）从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率。
18. （文科）已知动点P与平面上两定点
连线的斜率的积为定值
.
（1）试求动点P的轨迹方程C.
（2）设直线
与曲线C交于M、N两点，当MN=
时，求直线l的方程.
（理科）已知向量
=（0，x），
=（1，1），
=（x，0），
=（y2，1）（其中x，y是实数），
又设向量
=+
，
=－，且//，点P（x，y）的轨迹为曲线C.
（1）求曲线C的方程；
（2）设直线与曲线C交于M、N两点，当MN=时，求直线l的方程.
19．某承包户承包了两块鱼塘，一块准备放养鲫鱼，另一块准备放养鲤鱼，现知放养这两种鱼苗时都需要鱼料A、B、C，每千克鱼苗所需饲料量如下表：
| 鱼类 | 鱼料A | 鱼料B | 鱼料C |
| 鲫鱼/kg | | | |
| 鲤鱼/kg | | | |
如果这两种鱼长到成鱼时，鲫鱼和鲤鱼分别是当时放养鱼苗重量的30倍与50倍，目前这位承包户只有饲料A、B、C分别为
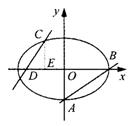20.已知椭圆
（a＞b＞0）的离心率
，过点A（0，-b）和B（a，0）的直线与原点的距离为
．
（1）求椭圆的方程．
（2）已知定点E（-1，0），若直线y＝kx＋2（k≠0）与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点?请说明理由．
21.甲乙两个围棋队各 5 名队员按事先排好的顺序进行擂台赛，双方 1 号队员先赛，负者被淘汰，然后负方的队员 2 号队员再与对方的获胜队员再赛，负者又被淘汰，一直这样进行下去，直到有一方队员全被淘汰时，另一方获胜．假设每个队员的实力相当，求甲方有 4 名队员被淘汰且最后战胜乙方的概率 ．
22. 已知椭圆C1的方程为
，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点。
（1）求双曲线C2的方程；
（2）若直线l：
与椭圆C1及双曲线C2恒有两个不同的交点，且l与C2的两个交点A和B满足
(其中O为原点)，求k的取值范围。
湖北随州曾都一中05—06学年高二上学期期末调研
数学试题答卷纸
| 题号 | 一 | 二 | 三 | 得分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 分数 | |||||||||
选择题答题卡
一．选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
非选择题
二．填空题 13. ________________________； 14. ________________________；
15. ________________________； 16. ________________________.
三．解答题
| 17.（本题满分12分） |
请在各题规定的黑色矩形区域内答题，超出该区域的答案无效！
| 18.（本题满分12分） |
请在各题规定的黑色矩形区域内答题，超出该区域的答案无效！
| 19.（本题满分12分） |
| 20.（本题满分12分） |
请在各题规定的黑色矩形区域内答题，超出该区域的答案无效！
| 21.（本题满分12分） |
| 22.（本题满分14分） |
请在各题规定的黑色矩形区域内答题，超出该区域的答案无效！
参考答案
一、选择题;DDABD AABBC DB
二、填空题：
； 
； 
； 240
三、解答题17.（1）记“摸出两个球，两球恰好颜色不同”为A，摸出两个球共有方法C
=10种，其中，两球一白一黑有C
·C
=6种， 
所求的概率为：P（A）=
=
…………………………5分
（2）记摸出一球，放回后再摸出一个球“两球恰好颜色不同”为B，摸出一球得白球的概率为
=0.4, 摸出一球得黑球的概率为=0.6，“有放回摸两次，颜色不同”指“先白再黑”或“先黑再白”，
所求的概率为：P（B）=0.4×0.6+0.6×0.4=0.48
………………12分
18.（文科）⑴解：设点
，则依题意有
，………3分
整理得
由于
，所以求得的曲线C的方程为
………………………………………5分
⑵同理科⑵
（理科）（1）由已知，
…………………………2分
即所求曲线的方程是：
…………………………5分
（2）由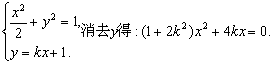
解得x1=0, x2=
分别为M，N的横坐标）.……………………9分
由
………11分
所以直线l的方程x－y+1=0或x+y－1=0.………………………………12分
19．[解析]：设放养鲫鱼xkg,鲤鱼ykg,则成鱼重量为
,其限制条件为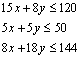 
………………………5分
画出其表示的区域（如图），不难找出使30x+50y最大值为
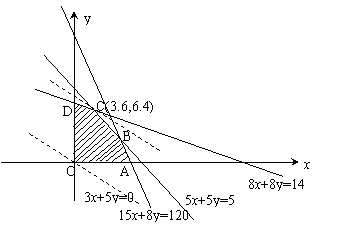答：鲫鱼放养
20.解析：（1）直线AB方程为：bx-ay-ab＝0．
依题意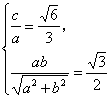
解得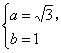 
∴ 椭圆方程为 
．…………………………4分
（2）假若存在这样的k值，由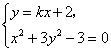
得
．
∴ 
． ①
设
，
、
，
，则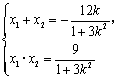
② …………8分
而
．
要使以CD为直径的圆过点E（-1，0），当且仅当CE⊥DE时，则
即
．………………………10分
∴ 
． ③
将②式代入③整理解得
．经验证，，使①成立．
综上可知，存在，使得以CD为直径的圆过点E．………………12分
21.解析：根据比赛规则可知，一共比赛了 9 场，并且在最后一场是甲方的 5 号队员战胜乙方的 5 号队员，而甲方的前 4 名队员在前 8 场比赛中被淘汰，也就是在 8 次独立实验中，甲方队员负 4 次，根据 8 次重复独立实验中该事件恰好发生 4 次的概率公式得 
，………………………8分
又第 9 场甲方的 5 号队员战胜乙方的 5 号队员的概率为 
．所以甲方有 4 名队员被淘汰且最后战胜乙方的概率是 
．………………………12分
22解：（1）设双曲线C2的方程为
，则
故C2的方程为
………………………………………………5分
（2）将
由直线l与椭圆C1恒有两个不同的交点得
即
①…………7分
.
由直线l与双曲线C2恒有两个不同的交点A，B得
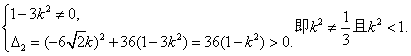…………………9分
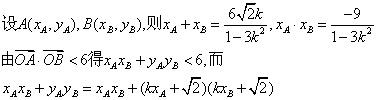
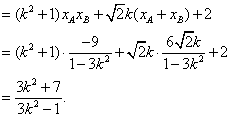
解此不等式得
③…………12分
由①、②、③得
故k的取值范围为
………………………14分