极坐标的练习

1.极坐标方程ρ=1表示(　　 )

A　直线　　　　 B射线　　　　  C圆　　　　  D椭圆

2.极坐标方程sinθ= (ρ∈R)表示的曲线是(　　  )

A两条相交直线　　　　  B两条射线

C一条直线　　　　　　  D一条射线

3.若极坐标方程ρ=ρ(θ)满足ρ(θ)= ρ(π-θ),则ρ=ρ(θ)表示的图形（　　）

A关于极轴对称　　　　　B关于极点对称

C关于射线θ=对称　　 D不确定

4.极坐标方程ρ=sinθ＋cosθ表示的曲线是（　　  ）

A直线　　　　  B圆　　　　　 C椭圆　　　　　 D抛物线

5. 极坐标方程ρ=cos(-θ)所表示的曲线是（　　　）

A 双曲线　　　　B椭圆　　　　 C抛物线　　　　  D 圆

6. 极坐标方程ρ=cosθ和ρ=sinθ的两个圆的圆心距是（　　　 ）

A　2　　　　　  B 　　　　　C　1　　　　　  D　

7.已知曲线C与曲线ρ=cosθ－5sinθ关于极轴对称，则曲线C的方程是（　　）

A ρ=-10cos（） 　　　　　　 Bρ=10cos（）

Cρ=-10cos（）　　　　　　　 Dρ=10cos（）

8.极坐标平面内，集合P=｛（ρ，θ）︳sinθ=，ρ∈R｝与集合S=｛（ρ，θ）︳cosθ=，ρ∈R｝之间的关系是（　　　 ）

A　PS　　　　B　PS　　　　  C P=S　　　　 D　PS=｛(0,0)｝

9.在极坐标系中，已知一个圆的方程为ρ=12sin（）,则过圆心与极轴垂直的直线的极坐标方程是（　　　 ）

A ρsinθ=　　Bρsinθ=-　 Cρcosθ=-3　　  D  ρcosθ=3

10在极坐标系中,过点A(6,π)作圆ρ=-4cosθ的切线，则切线长为（　　  ）

A  2　　　 B　6　　　 C  　　 D　

11.以极坐标系中的点（1，1）为圆心，1为半径的圆的方程是（　　　 ）

A ρ=2cos（）　　　　　　 B ρ=2sin（）

 C ρ=2cos（）　　　　　　  Dρ=2sin（）

12.极坐标方程ρ=2sinθ＋4cosθ表示的曲线是（　　  ）

A直线　　　　  B圆　　　　　 C双曲线　　　　 D抛物线.

13极坐标方程θ=的直角坐标方程是

14. θ=0，θ= （ρ≥0）和ρ=4所围成的面积是

15.极坐标方程ρcosθ=sin2θ所表示的曲线是

16.过点A(-2, )且与极轴平行的直线的极坐标方程是

17.已知定点A(a,0),动点P对极点O和点A的张角∠OPA=,在OP的延长线上取一点Q,使

　 ︳PQ ︳=︳PA ︳,当P在极轴上方运动时,求点Q的轨迹的极坐标方程.

答案

1-5　 CACBD　　　　 6-10　DBCCC　11-12 CB

13　y=－x　　 14　　 15　cosθ=0 (θ=或θ=)或ρ=2sinθ

16　ρsinθ=－　

17　解：设动点Q的坐标为（ρ，θ）则∠OQA=，在△OQA中，∠QAO=

　　　　由正弦定理可知：=

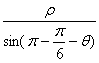
　　　　 ∴ρ=2asin()

　　　　 即：ρ=2asin（+θ）