伯乐园高二特色卷
(试卷总分:150分考试时间:120分钟)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的.
1.抛物线y2=ax的准线方程为x=-1,则a的值是( )
A.-2 B.
2.在下列各点中,位于不等式2x+3y<5表示的平面区域外的点是( )
A.(0,1) B.(1,0) C.(0,2) D.(2,0)
3.已知0<a<b<c, b<0且满足![]() ,则下列不等式中成立的是( )
,则下列不等式中成立的是( )
A.c<b<a B.a<b<c
C.b<a<c D.b<c<a
4.袋中有5个白球,3个黑球,从中任意摸出4个球,则至少摸到一个黑球的概率是( )
A.![]()
![]() B.
B.![]() C.
C. ![]() D.
D.![]()
5.将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD的中点,则异面直线AE、BC所成角的正切值是( )
A.![]() B.
B. ![]() C.2
D.
C.2
D. ![]()
6.二项式![]() 的展开式中含有x4
的项,则n的一个可能值是(
)
的展开式中含有x4
的项,则n的一个可能值是(
)
A.3
B
7.从一块短轴长为2b的椭圆形的玻璃镜中划出一块面积最大的矩形,其面积的取值范围是[3b2,4b2],则这一椭圆离心率e的取值范围是( )
A.[![]() ,
,![]() ] B.[
] B.[![]() ,
,![]() ]
]
C.[![]() ,
,![]() ] D.[
] D.[![]() ,
,![]() ]
]
8.球O的截面把垂直于截面的直径分成1∶3的两部分,若截面圆半径为![]() ,则球O的体积为(
)
,则球O的体积为(
)
A.16![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.从6人中选出4人参加数、理、化、英语比赛,每人只能参加其中一项,其中甲、乙两人都不能参加英语比赛,则不同的参赛方式共有( )
A.96种 B.180种 C.240种 D.288种
10.连续投掷两次骰子,以先后得到的两次点数m,n为点P(m,n)的坐标,则点P落在圆x2+y2=17外部的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
11椭圆![]() (a> b >0) 有内接正n边形 ,则n的所有可能值是 ( )
(a> b >0) 有内接正n边形 ,则n的所有可能值是 ( )
(A) 4 (B) 3,4 (C) 3,4,5 (D) 3,4,6
12.已知点P是双曲线![]() 右支上的动点,又知定点A(8,1) , 右焦点为F, 则
右支上的动点,又知定点A(8,1) , 右焦点为F, 则![]() 的值的范围是( )
的值的范围是( )
A.[1,+∞) B.![]() C.
C. ![]() D.[8, +∞)
D.[8, +∞)
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
13.有n(n∈N*)件不同的产品排成一排,若其中A、B两件产品排在一起的不同排法共有48种,则n= .
14.设x、y满足约束条件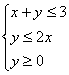 ’则目标函数Z=2x+y的最大值是 .
’则目标函数Z=2x+y的最大值是 .
15.不等式loga(x2-2x+3)≤-1在x∈R上恒成立,则实数a的取值范围为 .
16.能使不等式![]() 成立的正整数n的取值集合是
.
成立的正整数n的取值集合是
.
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
已知关于x的不等式![]() 的解集为M.
的解集为M.
(Ⅰ)当a=4时,求集合M;
(Ⅱ)若3∈M且5![]() M,求实数a的取值范围.
M,求实数a的取值范围.
18.(本小题满分12分)
已知抛物线的顶点在原点,它的准线过双曲线![]() 的一个焦点,并且这条准线与双曲线的两焦点连线垂直,又抛物线与双曲线交于点(
的一个焦点,并且这条准线与双曲线的两焦点连线垂直,又抛物线与双曲线交于点(![]() ,
,![]() ),求抛物线的方程和双曲线的方程.
),求抛物线的方程和双曲线的方程.
19.(本小题满分12分)
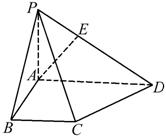 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=
(Ⅰ)求异面直线AE与CD所成角的大小;
(Ⅱ)求点C到平面PBD的距离.
20.(本小题满分12分)
将一个各个面上均涂有红颜色的正方体锯成64个同样大小的小正方体.
(Ⅰ)从这些小正方体中任取1个,其中恰好有奇数个面涂有红颜色的概率是多少?
(Ⅱ)从这些小正方体中任取2个,至少有一个小正方体的某个面或某几个面涂有红色的概率是多少?
21.(本小题满分12分)
如图,在长方体ABCD—A1B
(1)证明:D1E⊥A1D;
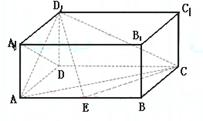 (2)当E为AB的中点时,求点E到面ACD1的距离;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC—D的大小为![]() .
.
22.(本小题满分14分)
已知A(-2,0),B(2,0),点C、D满足![]() =2,
=2,![]() =
=![]()
(Ⅰ)求点D的轨迹方程;
(Ⅱ)过点A作直线l交以A、B为焦点的椭圆于M、N两点,线段MN的中点到y轴的距离为![]() ,且直线l与点D的轨迹相切,求该椭圆的方程.
,且直线l与点D的轨迹相切,求该椭圆的方程.
试题答案
1.D 2.C 3.A 4.B 5.A 6.C 7. B 8.C 9.C 10.D 11.B 12.C
13.5 14.6 15.![]() 16.
16.![]()
17.解:(Ⅰ)当a=4时,原不等式为![]() (2分) 即
(2分) 即
4(x-![]() ) (x+2)(x-2)<0 (3分)
) (x+2)(x-2)<0 (3分)
解得x<-2或![]() <x<2 (5分)
<x<2 (5分)
故M={xx<-2或![]() <x<2}(6分)
<x<2}(6分)
(Ⅱ)由于3∈M , 故![]() ① (8分)
① (8分)
又5![]() M,故
M,故![]() ② (10分)
② (10分)
联立①②解得1≤a<![]() 或9<a<25(12分)
或9<a<25(12分)
18.法一:解:设抛物线方程为 y2=2px.因点(![]() ,
,![]() )在抛物线上,
)在抛物线上,
则6=2p·![]() ,得p=2.,抛物线方程为 y2=4x,(5分)
,得p=2.,抛物线方程为 y2=4x,(5分)
又双曲线左焦点在抛物线准线 x=-1上,故c=1 (7分)
从而 a2+b2=1 ① (8分)
将点(![]() ,
,![]() )代入双曲线方程得
)代入双曲线方程得![]() ② (9分)
② (9分)
由①、②解得 a2=![]() ,b2=
,b2=![]() , (11分)
, (11分)
故双曲线方程为
4x2-![]() y2=1.
(12分)
y2=1.
(12分)
法二:求出抛物线方程y2=4x,同解法一,
又双曲线左焦点在抛物线准线 x=-1上,故双曲线的焦点坐标为F1(-1,0),F2(1,0).由 得 a2=
得 a2=![]() .
.
所以b2=c2-
a 2=![]() . (11分)
. (11分)
故双曲线方程为 4x2-![]() y2=1.
(12分).
y2=1.
(12分).
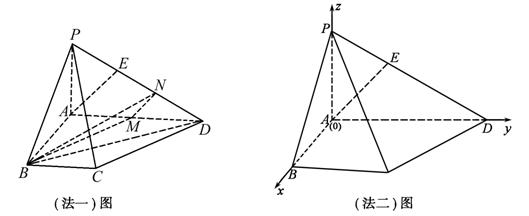
19.解:法一
(Ⅰ)取AD中点M,则BM∥CD,过M作MN∥AE,连BN,
则∠NMB为异面直线AE、CD所成的角或其补角,(2分)
由已知BM=![]() a,∵PD与底面成30°角,∴MN=
a,∵PD与底面成30°角,∴MN=![]() ,ND=
,ND=![]() ,PD=
,PD=![]() ,PA=
,PA=![]() ,
,
在Rt△ABD中,BD=![]() a, PB=
a, PB=![]() =
=![]() , PN=
, PN=![]() , ∴BN2=
, ∴BN2=![]()
在△BMN中,cos∠BMN=![]()
![]() =--
=--![]() (5分)
(5分)
由于异面直线所成角取值范围为(0,90°),
故所求角为arc
cos![]() . (6分)
. (6分)
(Ⅱ)
作AF⊥BD,BD=![]() a, AF=
a, AF=![]()
又PA=![]() , ∴PF=
, ∴PF=![]() , (9分)
, (9分)
S△PBD=![]() ,S△BCD=
,S△BCD=![]() ,VC-PBD=VP-BCD ,设点C到平面PBD的距离为d,则
,VC-PBD=VP-BCD ,设点C到平面PBD的距离为d,则
d·![]() =
=![]() ·
·![]()
![]() d=
d=![]() a (12分)
a (12分)
法二:
(Ⅰ)以A为空间直角坐标系原点,![]() 的方向为正方向建立直角坐标系如图
(2分)
的方向为正方向建立直角坐标系如图
(2分)
则 A(0,0,0),
C(a,a,0), D(0,![]() ,
,![]() a),
a),
∴![]() =(0,
=(0,![]() ,
,![]() a)
a)
![]() , cos(
, cos(![]() ,
,![]()
![]() )=
)=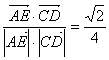
故所求角为
arc cos![]() (7分)
(7分)
(Ⅱ)设平面PBD的法向量
![]() =(x,y,z),P(0,0,
=(x,y,z),P(0,0,![]() a),∴
a),∴![]() ,
,![]()
由![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() 知
知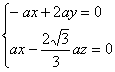
![]()
令z=a,得![]() =(
=(![]() a,
a,![]() ,a),又
,a),又![]() =(0,a,0),∴ d=
=(0,a,0),∴ d=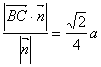 (12分)
(12分)
20.解:
(Ⅰ)小正方体中,有3个面,2个面,1个面,0个面涂有红色的个数分别为8,24,24,8
(4分)
故恰好有奇数个面涂有红色的概率为:
P1=![]() (6分)
(6分)
(Ⅱ)设![]() 表示所选取的2个小正方体都是0个面涂有红色的事件,则所求的概率为:
表示所选取的2个小正方体都是0个面涂有红色的事件,则所求的概率为:
P2=1-P(![]() )=1-
)=1-![]() (12分)
(12分)
21.解法(一)
(1)证明:∵AE⊥平面AA1 D1D ,A1D⊥AD1 ,∴ A1D⊥D1E (三垂线定理)(4分)。
(2)设点E到面ACD1的距离为h ,在△ACD1中,AC=CD1=![]() ,AD1=
,AD1=![]() ,
,
故![]()
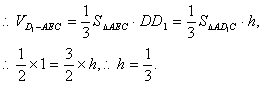
(8分)
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
∴∠DHD1为二面角D1—EC—D的平面角.
设AE=x,则BE=2-x
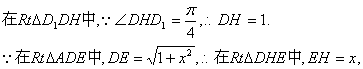
 (12分)
(12分)
解法(二):以D为坐标原点,直线DA,DC,DD1分别为x、y、z轴 ,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0),
C(0,2,0)
(1)![]() (4分)。
(4分)。
(2)因为E为AB的中点,则E(1,1,0),从而![]() ,
,
![]() ,设平面ACD1的法向量为
,设平面ACD1的法向量为![]() ,则
,则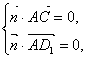
也即![]() ,得
,得![]() ,从而
,从而![]() ,所以点E到平面AD
,所以点E到平面AD
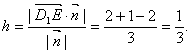 (8分)
(8分)
(3)设平面D1EC的法向量![]() ,∴
,∴![]()
由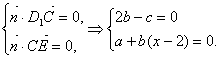 令b=1,
∴c=2,a=2-x,
令b=1,
∴c=2,a=2-x,
∴![]()
依题意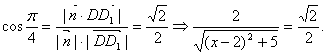
∴![]() (不合,舍去),
(不合,舍去),![]() .
.
∴AE=![]() 时,二面角D1—EC—D的大小为
时,二面角D1—EC—D的大小为![]() . (12分)
. (12分)
22.解:(Ⅰ)设C、D点的坐标分别为
C(x0,y0),D(x,y)
则![]() =(x0+2,y0),
=(x0+2,y0),![]() =(4,0)
=(4,0)
于是![]() +
+![]() =(x0+6,y0)
=(x0+6,y0)
故![]() =
=![]() (
(![]() +
+![]() )=(
)=(![]() ). (2分)
). (2分)
又![]() =(x+2,y)
=(x+2,y)
故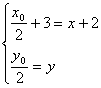 ,解得
,解得 (4分)
(4分)
代入![]() =
=![]() = 2
= 2
得x2+y2=1即为所求点D的轨迹方程. (7分)
(Ⅱ)易知直线l与x轴不垂直,设直线l的方程为 y=k(x+2) ①
又设椭圆方程为![]() (a2>4) ② (8分)
(a2>4) ② (8分)
又直线l与圆 x2+y2=1相切,故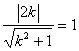 ,解得k2=
,解得k2=![]() (9分)
(9分)
将①代入②整理得(a2k2+a2-4)x2+
把k2代入上式得(a2-3)x2+a2x-![]() a4+
a4+
设M(x1,y1),N(x2,y2),则x1+x2=-![]() ,依题意有
,依题意有 ![]() =2×
=2×![]() (a2>3)得 a2=8 (13分)
(a2>3)得 a2=8 (13分)
经检验,此时△>0,故所求椭圆方程为![]() .(14分)
.(14分)
另解(I) 设C、D点的坐标分别为C(x0,y0),D(x,y)
由![]() =
=![]() 知,点D是线段BC的中点,
知,点D是线段BC的中点,
故x0=2x-2, y0=2y.点C的坐标为(2x-2,2y) (4分)
于是由![]() =2得,
=2得, ![]() =
=![]() , (6分)
, (6分)
化简得x2+y2=1即为所求点D的轨迹方程. (7分)
(II) 易知直线l与x轴不垂直,设y=k(x+2) ①
因直线l与圆 x2+y2=1相切,故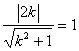 ,解得k2=
,解得k2=![]() (9分)
(9分)
由椭圆的对称性,不妨设直线l的方程为![]() . (1)
. (1)
设M(x1,y1),N(x2,y2),线段MN的中点P(x0,y0),依题意有x0=![]() 代入(1)式
代入(1)式
可求得y0= ![]() ,所以点P的坐标为(
,所以点P的坐标为(![]() ,
,![]() ). (11分)
). (11分)
又设椭圆方程为![]() .
.
于是 , (1)-(2)得
, (1)-(2)得![]() , 将(3)(4)代入
, 将(3)(4)代入
得![]() 即
即![]() ,再由
,再由![]() 知
知![]()
故所求椭圆方程为![]() . (14分)
. (14分)
