高二数学中期考试试题

总分150分　　时间120分钟

一、　　 选择题：(本大题共10小题，每小题5分，共50分)

 1、M＝｛正四棱柱｝，N＝｛长方体｝，Q＝｛正方体｝，P＝｛直四棱柱｝．则下列关系中正确的是　　　　　　　　　　　　　　　 　　　　　　　　　　　　 　　　　 （　　 ）

A、QMNP　 B、QMNP　　 C、QNMP　 　　D、QNMP

2、下列说法正确的是　　　　　　 　　　　　　　　　　　　　　　　　　 （　　 ）

A、直线a平行于平面M，则a平行于M内的任意一条直线

B、直线a与平面M相交，则a不平行于M内的任意一条直线

C、直线a不垂直于平面M，则a不垂直于M内的任意一条直线

D、直线a不垂直于平面M，则过a的平面不垂直于M

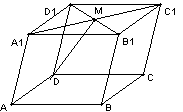3、如图：在平行六面体中，为与的交点。若，，，则下列向量中与相等的向量是　　　　　　　 （　　 ）

A、 　　　B、

C、 　　　D、

4、点（x，y，z）关于y轴的对称点的坐标是　　　　　　　　　　　　 （　　 ）

A、（x，-y，-z） 　B、（-x，-y，z）　  C、（x，-y，z）　　 D、（-x，y，-z）

5、已知空间四点 A（2，1，-3），B（-2，3，-4），C（3，0，1），D（1，4，m），

若A、B、C、D四点共面，则m=　　 　　　　　　　　　　　　　　　　（　　 ）

A、-7　　　　　　 B、-22　　　　　　 C、19　　　　 　　 D、5

6、下面四个条件：①平行于同一个平面；②垂直于同一直线；③与同一平面所成的角相

等；④分别垂直于两个平行平面. 其中能够判定空间两条直线平行的有　 （　　 ）　　　　　　　　 　　　　　　　　　　 

A．0个　　　　 　B．1个　　　　　 　C．2个　　　　 　D．3个

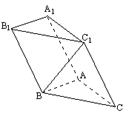7、如图，在斜三棱柱ABC－A₁B₁C₁中，∠BAC=90°，又BC₁⊥AC，过C₁作C₁H⊥底面ABC，垂足为H，则点H一定在　 (　　 )

A、直线AC上　　 　　 B、直线AB上　  

 C、直线BC上　　　　　D、△ABC的内部

8、若平面α∥平面β，直线在α内，且α与β之间的距离为d，下面给出四个命题：

①β内有且只有一条直线与的距离等于d；②β内所有直线与的距离都等于d；③β内

有无数条直线与的距离等于d；④β内所有直线与α的距离都等于d.其中正确的是 (　 )　　　　　　　　　　 A. ① B. ②　　　　　 　  C. ①与②　　　　　　　　　 D. ③与④

9、在下列条件中，可判断平面α与β平行的是　　　　　　　　　　　　　　　　（　　）

　　　　　　　　　　　A．α、β都垂直于平面.

　　　　　　　　　　　B．α内存在不共线的三点到β的距离相等.

　　　　　　　　　　　C．l，m是α内两条直线，且l∥β，m∥β.

　　　　　　　　　　　D．l，m是两条异面直线，且l∥α，m∥α, l∥β，m∥β.

10、一个棱锥被平行于底面的平面所截，若截面面积与底面面积之比为1：2，则此棱锥的高被分成两段之比（自上而下）为　　  　　　　　　　　　　　　　　　（　　 ）

A. 1：2　 　　　 B. 1：4； 　　　　　C. 1：（+1）　　　　 D. 1：（）

二、　　 填空题：（本大题共6小题，每小题4分，共24分，把正确答案填在题中横线上。）

11、边长为2的正方形ABCD的边CD在平面内，AB在平面外，如果AB与平面

的距离为，则对角线AC与平面所成角的大小是_____________.

12、已知S是△ABC所在平面外一点， D是SC的中点，若＝，

 则x＋y＋z＝　　　　　　 . 

13、正四面体ABCD中，点A（0，0，0），B（2，0，0），C（1，，0），则点D的坐标为________________.

14、设地球半径为R，若30°纬线圈 所在小圆的直径为AB，则A、B两点间的球面距离为__________________．

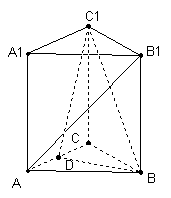
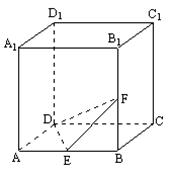
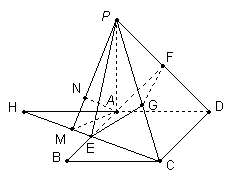
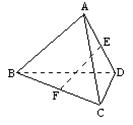15、如右图,在三棱锥A－BCD中，平面ABD⊥平面BCD，∠BDC＝90°，E、F分别是AD、BC的中点，若EF＝CD，则EF与平面ABD所成的角为___________．

16、下列5个正方体图形中，是正方体的一条对角线，点M、N、P分别为其所在棱的中点，能得出面MNP的图形的序号是　　　　 _________________________（写出所有符合要求的图形序号）

   ①　　　　　　  ②　　　　　　 ③　　　　　　　 ④　　　　　　 ⑤

三、解答题：（本大题共6小题，共76分,解答应写出文字说明，证明过程或或演算步骤)

17．（本小题满分12分）

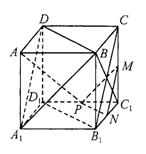 如图，在正方体ABCD-A₁B₁C₁D₁中，M、N、P分别是C₁C、B₁C₁、C₁D₁的中点，

求证：（1）AP⊥MN　　 　 （2）平面MNP∥平面A₁BD。

18. （本小题满分12分）

如图，正方体的一个顶点为O，OA、OB、OC是有一个公共点O的三个面上的对角线，OQ为正方体对角线。（1）求与的关系；（2）沿、、方向分别作用10g、20g、30g的力，求这些力的合力的大小。

19. （本小题满分12分）

已知正三棱柱ABC-A₁B₁C₁的底面边长为8，面的对角线BC₁=10，D为AC的中点，

（1）求证：AB₁//平面C₁BD；　（2）求异面直线AB₁与BC₁所成角的余弦值;

20. （本小题满分13分）

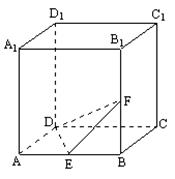
如图，正方体ABCD－A₁B₁C₁D₁中，E，F分别为AB与BB₁的中点，（1）求证：EF⊥平面A₁D₁B ； （2）求二面角F－DE－C大小．

21. （本小题满分13分）

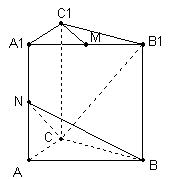
如图，直三棱柱ABC-A₁B₁C₁，底面△ABC中，CA=CB=1，∠BCA=90⁰，棱AA₁=2，M、N分别是A₁B₁，A₁A的中点，（1）求证：C₁M⊥BN　　 （2）求点B₁到平面CNB的距离；

22. （本小题满分14分）

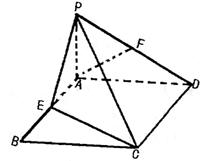
如图,PA⊥平面ABCD，四边形ABCD是矩形，点E在边AB上，F为PD的中点，AF∥平面PCE，（1）试确定E点位置；

（2）若二面角P-CD-B为45⁰，AD=2，CD=3，求直线AF到平面PCE的距离。

　　　　　　　　　　　 高二数学中期考试参考答案

一、　　 选择题：(本大题共10小题，每小题5分，共50分)　　 ABDDB，BCDDD

二、　　 填空题：（本大题共6小题，每小题4分，共24分）

11、30⁰ ； 12、 0 ； 13、 （1，，）；14、  15、30°；16、①④⑤

提示： 13、设D（x，y，z），由AB⊥CD，AD⊥BC，AD=2 ，可建立关于x，y，z的方程组，从而得解.

三、　　 解答题：（本大题共6小题，共76分）

17．（本小题满分12分）

证明：（1）连BC₁、B₁C，则B₁C⊥BC₁，BC₁是AP在面BBCC₁上的射影。

∴AP⊥B₁C，又B₁C∥MN，∴PA⊥MN；

（2）连结B₁D₁，∵P、N分别是D₁C₁、B₁C₁的中点，

∴PN∥B₁D₁,又B₁D₁∥BD，∴PN∥BD，又PN不在平面A₁BD上，　　∴PN∥平面A₁BD。

同理MN∥平面A₁BD，又PN∩MN=N，∴平面PMN∥平面A₁BD。

18. （本小题满分12分）

　 解：⑴设正方体的棱长为1，由图中坐标系可得：

A（1，1，0），B（1，0，1），C（0，1，1），Q（1，1，1）

∴=（2，2，2），=（1，1，1），

 则=2　　　　　　　 

⑵ ∵OA、OB、OC是有一个公共点O的三个面上的对角线，

∴、、两两夹角均为60⁰，

又∵沿、、方向分别作用10g、20g、30g的力，

∴可设=10，=20，=30，　　　　　　　

∵²=（）²=2500

∴=50，则这些力的合力的大小为50g　　

19. （本小题满分12分）

 解：（1）连结B₁ C交BC₁于点E，则E为BC₁的中点，并连结DE

∵D为AC中点　　∴DE∥AB₁　 而DE面BC₁D， AB₁面BC₁D　 ∴AB₁∥面C₁BD　　　　

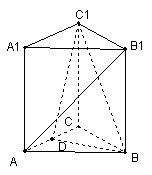（2）由（1）知AB₁∥DE，则∠DEB或其补角为异面直线AB₁与BC₁所成的角　　　　 

由条件知BC₁=10， BC=8　 则BB₁=6

∵正三棱柱中 AB₁=BC₁　　　∴DE=5

又∵BD=　　　　　 

∴在△BED中 

　故异面直线AB₁与BC₁所成角的余弦值为

解二（向量法）以点D为原点，以、、方向的单位向量为x、y、z轴建立空间直角坐标系，由已知得A（4，0，0），B（0，4，0），C（-4，0，0），

D（0，0，0），A₁（4，0，6），B₁（0，4，6），C（-4，0，6），

则=（-4，4，6），=（-4，-4，6）.　　　　 

设平面C₁BD的法向量为=（x，y，z），由•=0，可得 y=0；

由•=0，可得4x=10z，∴可取=（5，0，2），　　　　　

（1）∵•=0 ，∴AB₁∥面C₁BD 　　　　　　　　　　　　 

（2）∵cos<，>=　　　　　　 故异面直线AB₁与BC₁所成角的余弦值为

20. （本小题满分13分）　（1）

（II）延长DE、CB交于N，∵E为AB中点，

∴△DAE≌△NBE

过B作BM⊥EN交于M，连FM，∵FB⊥平面ABCD

∴FM⊥DN，∴∠FMB为二面角F—DE—C的平面角　　　

设AB=a，则BM=　　又BF=

∴tan∠FMB=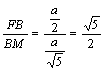，　　 即二面角F—DE—C大小为arctan　　　　　　　

证明二（向量法）：（1）以射线、、分别为OX、OY、OZ轴，建立空间直角坐标系，设正方体ABCD－A₁B₁C₁D₁棱长为2，则E（2，1，0），F（2，2，1），A₁（2，0，2），D₁（0，0，2），B（2，2，0）；=（0，1，1），=（-2，0，0），=（0，2，-2）.

　　　　　　　   由•=0，•=0 ，可得 EF⊥A₁D₁，　　EF⊥A₁B，∴EF⊥平面A₁D₁B（2）平面CDE的法向量为=（0，0，2），设平面DEF的法向量为

 =（x，y，z），由•=0，•=0 ，解得2 x= - y=z，

可取 =（1，-2，2），设二面角F－DE－C大小为θ，

∴cosθ=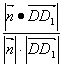==，即二面角F—DE—C大小为arccos

21. （本小题满分13分）

解一：（1）以射线、、分别为OX、OY、OZ轴，建立空间直角坐标系，

则 C₁（0，0，2），M（，，2），N（1，0，1），B（0，1，0），

=（，，0），=（1，-1，1）　　  

　　∴·=×1+×（-1）+0×1=0 ，∴ BN⊥C₁M

（2）=（1，0，1），（0，1，2），=（0，1，0），

设平面CNB的法向量为=（x，y，z），

由·=0 ，·=0，解得 y=0，x= - z，取=（1，0，-1），

记点B₁到平面CNB的距离d，　　　 ∴d==　　　

解二：（1）在直三棱柱ABC-A₁B₁C₁中，∵CA=CB=1，M是A₁B₁的中点，

∴C₁M⊥A₁B₁，又∵AA₁⊥平面A₁B₁C₁，∴C₁M⊥AA₁，

则C₁M⊥平面A₁B₁BA，又∵BN平面A₁B₁BA，∴C₁M⊥BN

 （2）∵B₁C₁∥BC，∴点B₁到平面CNB的距离d等于点C₁到平面CNB的距离.

　连C₁N，∵在矩形A₁C₁CA中，N是A₁A的中点，CA=CB=1， AA₁=2，

　∴C₁N⊥CN；又由C₁C⊥CB，AC⊥CB，得CB⊥平面A₁C₁CA，

∴CB⊥C₁N.　　　　 则C₁N⊥平面BCN，∴d=C₁N=.　　　　　　　　　

22. （本小题满分14分）

解：（1）过AF、AB作平面β交PC于点G，连FG、EG，

∵四边形ABCD是矩形，点E在边AB上，∴EA∥CD，

∴EA∥平面PCD， ∴EA∥FG∥CD，　

∵AF∥平面PCE，∴AF∥EG，　　　　则四边形AEGF是平行四边形

又∵F为PD的中点，∴EA=FG=CD，

 则点E是边AB的中点.　

（2）延长CE、DA交于点H，作AM⊥HC，垂足为点M；连接AM、PM，作AN ⊥PM，垂足为点N.

∵PA⊥平面ABCD，∴PA⊥HC，则HC⊥平面PAM，

∴HC⊥AN，则AN ⊥平面PEC；

又∵AF∥平面PCE，∴线段AN的长是直线AF到平面PCE的距离.　

∵二面角P-CD-B为45⁰，可证得∠PDA就是二面角P-CD-B的平面角，

∴∠PDA=45⁰.　　　在Rt△PAD中，∵AD=2，∴PA=2.

又在Rt△HCD中，∵EA =CD，CD=3，∴AH= AD=2.

∵AM⊥HC，∴Rt△HCD∽Rt△HAM，可求得AM=.

在Rt△PAM中，∵S_△PAM=PA•AM=AN•PM，　　　　　　　　　　  ∴AN=.　

解法二：以点A为原点，AB、AD、AP为X、Y、Z轴建立空间直角坐标系（如图），由已知可得A（0，0，0），B（3，0，0），D（0，2，0），C（3，2，0），

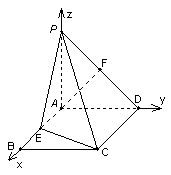∵二面角P-CD-B为45⁰，可证得∠PAD就是二面角P-CD-B的平面角，∴∠PDA=45⁰.

在Rt△PAD中， AD=2，∴PA=2，则P（0，0，2）

又∵F为PD的中点，∴F（0，1，1）

则=（0，1，1），=（3，2，-2） 

∵点E在边AB上，∴设E（λ，0，0），

 则=（3-λ，2，0）

设平面PEC的法向量=（x，y，z），由•=0得（3-λ）x+2y=0，

由•=0得3x+2y-2z=0，解得y=，z=；

令x=2，得=（2，λ-3，λ）　　　　　　　　　　　　

（1）∵AF∥平面PCE，∴•=0，即λ-3+λ=0，∴λ=

则点E是边AB的中点.　　　　　　　　　　　　　　　　

（2）∵AF∥平面PCE，∴直线AF到平面PCE的距离等于点A到平面PCE的距离d，则d=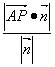==.