高中二年级数学(上)第七章第一单元测试题

时间：120分钟　　　　总分：150分

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1． 下列命题：

（1）直线的倾斜角为，则直线的斜率为；

（2）若直线的斜率为，则此直线的倾斜角为；

（3）任何一条直线都有倾斜角，但不是每一条直线都存在斜率；

（4）直线的倾斜为，则；

（5）直线的斜率为0，则直线的倾斜角为0或．

其中正确有（　　）

A．1个　　　　　　　 B．2个　　　　　　　 C．3个　　　　　　　D．4个

2． 直线平行于直线，且在轴上的截距为，则的值分别为（　  ）

A．和　　　　　　　　　　　　 B．和　　　　　　　　　　　　 C．和　　　　　　　　　　　　 D．和

3． 轴上一点到一、三象限平分线的距离为（　　）

A．　　　　　 B．　　　　　　　 C．　　　　　　　　D．

4． 已知直线，和轴，轴围成的四边形有外接圆，则实数等于（　  ）

A．1　　　　　　　　　　B．2　　　　　　　　　　C．3　　　　　　　　　 D．4

5． 若且，直线不通过（　  ）

A．第三象限　　　　　　　　  B．第一象限　　　　　　　　 C．第四象限 　　　　D．第二象限

6． 已知点，点在直线上，若直线垂直于直线，则点的坐标是（　  ）

A．　　　　　　B．　　　　　 C．　　　　　　　　　 D．

7． 若，则经过两点，的直线的倾斜角为（　　）

A．　　　　　　　　　 B．　　　　　　　 　　 C．　 　　　　　D．

8． 已知直线和的夹角平分线为，如果的方程为，那么的方程为（　  ）

A．　　　　 　　　　　  　 B．

C．　　　　　　　　　　　　　　  D．

9． 已知直线，当变化时，所有直线都经过的定点为（　　）

A．　　　　　　　 B．　　　　　　　　C．　　　　　　　　D．

10． 由5条直线：，，，，可以组成三角形的个数为（　　）

A．0　　　　　　　　　　B．2　　　　　　　　　　C．10　　　　　　　　　　　　　 D．以上都不对

11． 在直角坐标系中，已知的三边所在直线的方程分别是，，，则的内部和边上的整点（即横、纵坐标都为整数的点）的总数是（　　）

A．　　　　　　　　　　　　B．　　　　　　　　　　　　 C．　　　　　　　　　　　　D．

12． 已知等腰直角三角形斜边所在直线的方程，直角顶点坐标为，则两条直角边所在直线的方程分别为（　　）

A．　　　　　 B．

C．　　　　　  D．

二、填空题：本大题共4小题，每小题4分，共16分，把答案填写在题中横线上．

13． ，直线的倾斜角的变化范围是　　　　　．

14． 将直线绕点沿逆时针方向转动，则旋转后直线的方程是　　　　　　．

15． 已知直线的方向向量，若直线经过点且，则直线的方程为　　　　　　．

16． 若实数，满足，则的最大值、最小值分别为　　　　　　．

三、解答题：本大题共8小题，共74分，解答应写出必要的计算过程、推演步骤或文字说明．

17．(本小题8分) 当且仅当为何值时，经过两点，的直线的斜率为3？

18．(本小题8分) 直线经过点，它的倾斜角是直线倾斜角的2倍，求直线的方程．

　

　

　

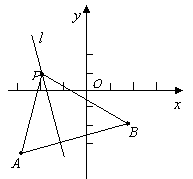19．(本小题8分) 已知，，，如图所示，若直线过点且与线段有公共点，试求直线的斜率的取值范围．

　　

　

　

　

20．(本小题8分) 求直线关于直线对称的直线方程．

　

 

　

21．(本小题8分) 求过点的直线使它与直线的夹角为．

22．(本小题10分) 两平行线，分别过点与，

⑴若与距离为，求两直线方程；

⑵设与之间距离是，求的取值范围．

23．(本小题12分) 已知直线与直线的倾斜角相等，并且与两坐标轴围成的三角形的面积为，求直线的方程．

　

　

 

24．(本小题12分) 光线从点射出，到轴上的点后被轴反射到轴上的点，又被轴反射，这时反射线恰好过点，求所在直线的方程．

　

　

高中二年级数学(上)第七章第一单元测试题答案

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1． B2． D3． B．4． C．5． C．6． C．7． C8． A9． C10． A．9． B11． A12

二、填空题：本大题共4小题，每小题4分，共16分，把答案填写在题中横线上．

13． ．14． ．15． ．16． ，．

三、解答题：本大题共8小题，共74分，解答应写出必要的计算过程、推演步骤或文字说明．

17．(本小题8分) 解：，

即，解得．

18．(本小题8分) 解：设直线的倾斜角为，则所求直线倾斜角为．

　　　 ，

　　　 所求直线的斜率．

　　　 所求直线方程为，即．

19．(本小题8分) 解：，

，

要使直线与线段有公共点，的取值范围应该是，或．

20．(本小题8分) 解：由得交点为．

设所求直线斜率为，由一条直线到另一条直线的角的公式得，．所以所求直线方程为．

21．(本小题8分) 解：已知直线的斜率为，设所求直线的斜率为．

　　　 由夹角公式得，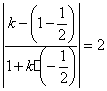

　　　 解得．所求的直线为．

　　　 又过点与轴平行的直线也符合要求．

　　　 直线方程为或．

22．(本小题10分) 解：⑴设的方程为，

则，解之得或．

的方程为或．

利用两平行直线间的距离公式可得的方程为或．

⑵显然这两条直线之间的最大距离即，两点之间的距离为，．

23．(本小题12分) 解：直线的斜率是，

与直线的倾斜角相等，

的斜率为．

设直线的方程为，的横截距为．

与两坐标轴围成的三角形面积为24，

，即．

直线的方程是，即．

24．(本小题12分) 解：点关于轴的对称点及点关于轴的对称点均在上，故的方程为，即．