高中学生学科素质训练
高二数学同步测试（9）—抛物线及几何性质
共150分，考试用时120分钟
一、选择题（本题每小题5分，共60分）
1．抛物线
的焦点坐标为
（ ）
A．
B．
C．
D．
2．过抛物线y2=4x的焦点作直线交抛物线于A（x1,y1）、B（x2,y2）两点，如果x1+x2=6，则AB的长是 （ ）
A．10 B．
3．抛物线y=x2上点A处的切线与直线
的夹角为45°，则点A的坐标是（ ）
A．（－1，1） B．
C．（1，1） D．（－1，1）或
4．设P是抛物线
上的动点，点A的坐标为（0，－1），点M在直线PA上，且分
所成的比为2：1，则点M的轨迹方程是 （ ）
A．
B．
C．
D．
5．已知抛物线
的焦点为F，定点P(4,－2)，在抛物线上找一点M，使得
最小，则点M的坐标为 （ ）
A．
B．
C．
D．
6．抛物线
上的点到直线
的距离最短，则该点的坐标为 （ ）
A．
B．
C．
D．
7．抛物线
上的点
到抛物线焦点的距离为3，则y0= （ ）
A．
B． C．2 D．4
8．过抛物线的焦点F作倾斜角是
的直线，交抛物线于A,B两点，则
（ ）
A．8 B．
C．
D．16
9．过抛物线焦点F的直线与抛物线交于P,Q两点，若P,Q在抛物线准线上的射影为
，
则
等于 （ ）
A．
B．
C．
D．
10．已知抛物线
上三点A,B,C,且A(－1,0),
当点B移动时，点C的横坐
标的取值范围是 （ ）
A．
B．
C．
D．
11．若一个圆的圆心在抛物线y2=4x的焦点处，且此圆与直线x+y+1=0相切，则这个圆的方程是 （ ）
A．x2+y2－2x－1=0 B．x2+y2+2x+1=0
C．x2+y2－2y+1=0 D．x2+y2+2y+1=0
12．设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是 （ ）
A．[－
，] B．[－2，2] C．[－1，1] D．[－4，4]
二、填空题（本题每小题4分，共16分）
13．若抛物线的顶点是双曲线
的中心，且准线与双曲线的左准线重合，则此抛
物线的方程为____________.
14．设x1, x2∈R定义运算×：x1×x2=(x1+x2)2－(x1－x2)2,若x≥0，常数m>0，则动点P(x,
)的轨迹方程是
15．一个正三角形的三个顶点都在抛物线上，其中一个顶点在原点，则这个三角形
的面积为_________.
16．AB是抛物线
的一条焦点弦，若
，则AB的中点到直线
的距
离为_____________.
三、解答题（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤）
17．（12分）.过点A(0，－2)的直线与抛物线相交于两点P,Q，求以OP,OQ为邻边
的平行四边形的第四个顶点M的轨迹方程．
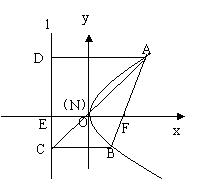
18．（12分）一辆卡车高3米，宽1.6米，欲通过抛物线型隧道，拱口宽恰好是抛物线的正焦弦长，若拱口宽为a米，求能使卡车通过的a的最小整数值．
 |
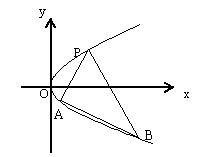
19．（12分）如图所示，设抛物线
的焦点为F，
经过F的直线交抛物线于A,B两点，点C在抛物线的准
线上，且BC//x轴，证明直线AC经过原点O．
20．（12分）、如图，过抛物线
上一定点
P（
）（
），作两条直线分别交抛物线于
A（
），B（
）
（I）求该抛物线上纵坐标为
的点到其焦点F的距离
（II）当PA与PB的斜率存在且倾斜角互补时，求
的值，并证明直线AB的斜率是非零常数
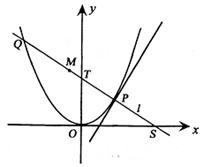
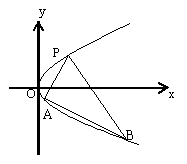
21．(12分)如图，P是抛物线C：y=x2上一点，直线l过点P且与抛物线C交于另一点Q.
（Ⅰ）若直线l与过点P的切线垂直，求线段PQ中点M的轨迹方程；
（Ⅱ）若直线l不过原点且与x轴交于点S，与y轴交于点T，试求
的取
值范围.
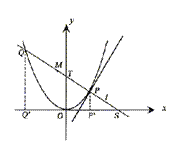
22．（14分）如图, 直线y=x与抛物线y=
x2－4交于
A、B两点, 线段AB的垂直平分线与直线y=－5交
于Q点.
（1）求点Q的坐标；
（2）当P为抛物线上位于线段AB下方(含点A、B) 的
动点时, 求△OPQ面积的最大值.
参考答案（9）
一．选择题 (本大题共12小题, 每小题5分, 共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | D | A | C | C | B | D | C | A | A | C |
二．填空题（本大题有4小题, 每小题4分, 共16分）
13．
14. y2=2mx(y≥0) 15. 
16. 
三、解答题（本大题共6题，共74分）
17．解 平行四边形 ABCD的对角线的交点为N，且
．由题
意得直线PQ的方程为
，其中k为不等于零的参数
由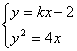
，得
，
N是PQ的中点
N点的坐标为
，又N为OM的中点
直线PQ和抛物线有两个不同的交点
式中
，解得：
由
，故点M的轨迹方程为
18．分析：先建立如图所示的坐标系，确定抛物线的方程，由对称性知，卡车的轴线与y轴重合，问题转化为求出x＝0.8时的y值，需y＞3才能满足条件．
解：设抛物线方程为x2＝－2p(y－p/2)∵（a/2，0）在抛物线上，∴a2/4＝p2 ，即p＝a/2．
从而抛物线方程为x2＝－a(y－a/4)，将（0.8,y）代入得
卡车高3米，故
需y＞3且a＞0，得 a2－12a－2.56＞0，解得a＞12.21或a＜－0.12（舍去）所以a应
取13．
注：本题以应用问题描述为载体，利用代定系数法求抛物线方程，解题中利用点与坐标、
曲线与方程的对应关系，融进参数的讨论，富有新意。
19．解：如图，连接AC，设AC与EF交于点N，过A作
于D，则AD//EF//BC，
,
由抛物线的定义：有
N是线段EF
的中点，即AC经过点O
20．解：本小题主要考查直线、抛物线等基本知识，考查运用解析几何的方法分析问题和解决问题的能力.满分14分.
解：（I）当
时，
, 又抛物线
的准线方程为
. 由抛物线定义得，所求距离
为
.
（2）设直线PA的斜率为
，直线PB的斜率为
由
，
,
相减得
.
故
. 同理可得
.
由PA，PB倾斜角互补知
,
即
, 所以
, 故
.
设直线AB的斜率为
由
，
相减得
, 所以
.
将
代入得 
，所以是非零常数.
21．解：本题主要考查直线、抛物线、不等式等基础知识，求轨迹方程的方法，解析几何的基本思想和综合解题能力.满分12分.
解：（Ⅰ）设P(x1，y1)，Q(x2，y2)，M(x0，y0)，依题意x1≠0，y1>0，y2>0.
由y=x2， ①得y＇=x.∴过点P的切线的斜率k切= x1，
∵x1=0不合题意，∴x1≠0∴直线l的斜率
∴直线l的方程为y－x12=－
(x－x1)，
方法一：联立①②消去y，得x2+
x－x12－2=0.∵M是PQ的中点
∴ x0=
=－， y0=x12－(x0－x1).
消去x1，得y0=x02+
+1(x0≠0)，∴PQ中点M的轨迹方程为y=x2++1(x≠0).
方法二：由y1=x12，y2=x22，x0=，
得y1－y2=x12－x22=(x1+x2)(x1－x2)=x0(x1－x2)，则x0=
=kl=－，
∴x1=－
，将上式代入②并整理，得
y0=x02++1(x0≠0)，∴PQ中点M的轨迹方程为y=x2++1(x≠0).
（Ⅱ）设直线l:y=kx+b，依题意k≠0，b≠0，则T(0，b).分别过P、Q作PP＇⊥x轴，
＇⊥y轴，垂足分别为P＇、Q＇，则
.
y=x2
由 消去x，得y2－2(k2+b)y+b2=0. ③
y=kx+b
y1+y2=2(k2+b)，
则
y1y2=b2.
方法一：
∴b(
)≥2b
=2b
=2.
∵y1、y2可取一切不相等的正数，∴的取值范围是（2，+
）.
方法二：
∴=b
=b
.
当b>0时，=b=
=
+2>2；
当b<0时，=－b=
.
又由方程③有两个相异实根，得△=4(k2+b)2-4b2=4k2(k2+2b)>0，
于是k2+2b>0，即k2>－2b.
所以>
=2.
∵当b>0时，可取一切正数，∴的取值范围是（2，+）.
22．解：(1) 解方程组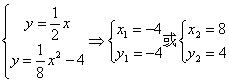 
即A(－4,－2),B(8,4),
从而AB的中点为M(2,1). 由kAB==,直线AB的垂直平分线方程y－1=(x－2).
令y=－5, 得x=5,
∴Q(5,－5) (2) 直线OQ的方程为x+y=0, 设P(x, x2－4).
∵点P到直线OQ的距离d=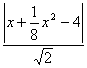
=
, 
,
∴SΔOPQ=
=
. ∵P为抛物线上位于线段AB下方的点, 且P不
在直线OQ上, ∴－4≤x<4
－4或4－4<x≤8. ∵函数y=x2+8x－32在区间
[－4,8] 上单调递增, 且当x=－4时，x2+8x－32=48 当x=8时，x2+8x－32=96
∴当x=8时, ΔOPQ的面积取到最大值
.