高中学生学科素质训练
高二数学同步测试(10)—圆锥曲线综合应用及光学性质
共150分,考试用时120分钟
一、选择题(本大题共12小题,每小题5分,共60分)
1.二次曲线![]() ,
,![]() 时,该曲线的离心率e的取值范围是 ( )
时,该曲线的离心率e的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.我国发射的“神舟3号”宇宙飞船的运行轨道是以地球的中心![]() 为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为
( )
为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为
( )
A.![]() B.
B.![]()
C.mn D.2mn
3.已知椭圆![]()
![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,且
,且![]() ,弦AB过点
,弦AB过点![]() ,则△
,则△![]() 的周长为 ( )
的周长为 ( )
A.10 B.![]() D.
D. ![]()
4.已知椭圆的中心在原点,离心率![]() ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线![]() 的焦点重合, 则此椭圆方程为 ( )
的焦点重合, 则此椭圆方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围 ( )
A.[-![]() ,
,![]() ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
6.以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是 ( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
7.椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点![]() 、
、![]() 是它的焦点,长轴长为
是它的焦点,长轴长为![]() ,焦距为
,焦距为![]() ,静放在点
,静放在点![]() 的小球(小球的半径不计),从点
的小球(小球的半径不计),从点![]() 沿直线出发,经椭圆壁反弹后第一次回到点
沿直线出发,经椭圆壁反弹后第一次回到点![]() 时,小球经过的路程是
( )
时,小球经过的路程是
( )
A.![]() B.
B.![]() C.
C.![]() D.以上答案均有可能
D.以上答案均有可能
8.过双曲线![]() 的右焦点F2有一条弦PQ,PQ=7,F1是左焦点,那么△F1PQ的周长
的右焦点F2有一条弦PQ,PQ=7,F1是左焦点,那么△F1PQ的周长
为 ( )
A.28
B.![]() C.
C.![]() D.
D.![]()
9.已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和![]() .若
.若![]() 是
是![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率是 ( )
的等差中项,则椭圆的离心率是 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
10.过抛物线![]() (a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长
(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长
分别为p、q,则![]() 等于 ( )
等于 ( )
A.![]() C.
C.![]()
![]() D.
D.![]()
11.如果椭圆![]() 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.设P(x ,
y) (xy≠0)是曲线![]() 上的点,F1(-4,0
) 、F2(4,0), 则 ( )
上的点,F1(-4,0
) 、F2(4,0), 则 ( )
A.F1 P + F2 P <10 B.F1 P + F2 P >10
C.F1 P + F2 P ≥10 D.F1 P + F2 P ≤10
二、填空题(本大题共4小题,每小题4分,共16分)
13.设中心在原点的椭圆与双曲线![]() =1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是
.
=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是
.
14.设![]() 是曲线
是曲线![]() 上的一个动点,则点
上的一个动点,则点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到
到![]() 轴的距离之和的最小值为
.
轴的距离之和的最小值为
.
15.与椭圆![]() 具有相同的离心率且过点(2,-
具有相同的离心率且过点(2,-![]() )的椭圆的标准方程是
.
)的椭圆的标准方程是
.
16.设双曲线![]() 的半焦距为c,直线过(a,0)、(0,b)两点,已知原
的半焦距为c,直线过(a,0)、(0,b)两点,已知原
点到直线L的距离为![]() ,则双曲线的离心率为 .
,则双曲线的离心率为 .
三、解答题(本大题共6题,共74分)
17.(本题满分10分) 已知双曲线与椭圆![]() 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为![]() ,
,
求双曲线方程.
18.(本题满分10分)、求两条渐近线为![]() 且截直线
且截直线![]() 所得弦长为
所得弦长为![]()
的双曲线方程.
19.(本题满分13分).双曲线![]() 的焦距为
的焦距为![]() 过点(a,0)
过点(a,0)
和(0,b),且点(1,0)到直线![]() 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线![]() 的距离之和
的距离之和![]() 求
求
双曲线的离心率e的取值范围.
20.(本题满分13分)设椭圆![]() 的两个焦点是
的两个焦点是![]() 与
与![]() ,且椭圆上存在一点
,且椭圆上存在一点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是相应于焦点
是相应于焦点![]() 的准线,直线
的准线,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,
,
求直线![]() 的方程.
的方程.
21.(本题满分14分).给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点.
(Ⅰ)设l的斜率为1,求![]() 与
与![]() 的夹角的大小;
的夹角的大小;
(Ⅱ)设![]() ,若λ∈[4,9],求l在y轴上截距的变化范围..
,若λ∈[4,9],求l在y轴上截距的变化范围..
|
(1)设P、Q两点坐标分别为(x1,y1)、(x2,y2),
证明:y1·y2=-p2;
(2)求抛物线的方程;
(3)试判断在抛物线上是否存在一点,使该点与点
M关于PN所在的直线对称?若存在,请求出
此点的坐标;若不存在,请说明理由.
参考答案(10)
一.选择题 (本大题共12小题, 每小题5分, 共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | D | A | C | D | D | C | A | C | D | D |
7【解】⑴静放在点![]() 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点![]() 沿直线出发,经椭圆壁右顶点反弹后第一次回到点
沿直线出发,经椭圆壁右顶点反弹后第一次回到点![]() 时,小球经过的路程是
时,小球经过的路程是![]() ,则选B;
,则选B;
⑵静放在点![]() 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点![]() 沿直线出发,经椭圆壁左顶点反弹后第一次回到点
沿直线出发,经椭圆壁左顶点反弹后第一次回到点![]() 时,小球经过的路程是
时,小球经过的路程是![]() ,则选C;
,则选C;
⑶静放在点![]() 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点![]() 沿直线出发,经椭圆壁非左右顶点反弹后第一次回到点
沿直线出发,经椭圆壁非左右顶点反弹后第一次回到点![]() 时,小球经过的路程是
时,小球经过的路程是![]() ,则选A。
,则选A。
于是三种情况均有可能,故选D。
二.填空题(本大题有4小题, 每小题4分, 共16分)
13.![]() 14.
14. ![]() 15.
15. ![]() 或
或![]() 16. 2
16. 2
三、解答题(本大题共6题,共74分)
17.(本题满分10分)解:由于椭圆焦点为F(0,![]() 4),离心率为e=
4),离心率为e=![]() ,所以双曲线的焦点为F(0,
,所以双曲线的焦点为F(0,![]() 4),离心率为2,
4),离心率为2,
从而c=4,a=2,b=2![]() . 所以求双曲线方程为:
. 所以求双曲线方程为: ![]() .
.
18(本题满分10分)解:设双曲线方程为x2-4y2=![]() .
.
联立方程组得: 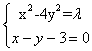 ,消去y得,3x2-24x+(36+
,消去y得,3x2-24x+(36+![]() )=0
)=0
设直线被双曲线截得的弦为AB,且A(![]() ),B(
),B(![]() ),那么:
),那么: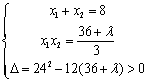
那么:AB=![]()
解得: ![]() =4,所以,所求双曲线方程是:
=4,所以,所求双曲线方程是:![]() .
.
19.(本题满分13分)
解:直线![]() 的方程为
的方程为![]() ,即
,即 ![]()
由点到直线的距离公式,且![]() ,得到点(1,0)到直线
,得到点(1,0)到直线![]() 的距离
的距离![]() ,
,
同理得到点(-1,0)到直线![]() 的距离
的距离![]()
![]()
由![]() 即
即 ![]()
于是得 ![]()
解不等式,得 ![]() 由于
由于![]() 所以
所以![]() 的取值范围是
的取值范围是![]()
20.(本题满分13分)本小题主要考查直线和椭圆的基本知识,以及综合分析和解题能力.
解:(Ⅰ)由题设有![]() 设点P的坐标为
设点P的坐标为![]() 由PF1⊥PF2,得
由PF1⊥PF2,得
![]() 化简得
化简得 ![]() ①
①
将①与![]() 联立,解得
联立,解得 ![]()
由![]() 所以m的取值范围是
所以m的取值范围是![]() .
.
(Ⅱ)准线L的方程为![]() 设点Q的坐标为
设点Q的坐标为![]() ,则
,则
![]()
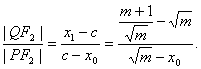 ②
②
将
![]() 代入②,化简得
代入②,化简得 ![]()
由题设 ![]() ,得
,得 ![]() , 无解.
, 无解.
将
![]() 代入②,化简得
代入②,化简得 ![]()
由题设
![]() ,得
,得 ![]() .
.
解得m=2. 从而![]() ,
,
得到PF2的方程 ![]()
21.(本题满分14分)本小题主要考查抛物线的性质,直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力.
解:(Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为![]()
将![]() 代入方程
代入方程![]() ,并整理得
,并整理得 ![]()
设![]() 则有
则有 ![]()
![]()
![]()
![]()
所以![]() 夹角的大小为
夹角的大小为![]()
(Ⅱ)由题设![]() 得
得 ![]()
|
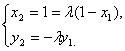
由②得![]() , ∵
, ∵ ![]() ∴
∴![]() ③
③
联立①、③解得![]() ,依题意有
,依题意有![]()
∴![]() 又F(1,0),得直线l方程为
又F(1,0),得直线l方程为
![]()
当![]() 时,l在方程y轴上的截距为
时,l在方程y轴上的截距为![]()
由 ![]() 可知
可知![]() 在[4,9]上是递减的,
在[4,9]上是递减的,
∴
![]()
直线l在y轴上截距的变化范围为![]()
22.(本题满分14分)命题意图:对称问题是直线方程的又一个重要应用.本题是一道与物理中的光学知识相结合的综合性题目,考查了学生理解问题、分析问题、解决问题的能力。
知识依托:韦达定理,点关于直线对称,直线关于直线对称,直线的点斜式方程,两点式方程.
错解分析:在证明第(1)问题,注意讨论直线PQ的斜率不存在时.
技巧与方法:点关于直线对称是解决第(2)、第(3)问的关键.
(1)证明:由抛物线的光学性质及题意知
光线PQ必过抛物线的焦点F(![]() ,0),
,0),
设直线PQ的方程为y=k(x-![]() )
①
)
①
由①式得x=![]() y+
y+![]() ,将其代入抛物线方程y2=2px中,整理,得y2-
,将其代入抛物线方程y2=2px中,整理,得y2-![]() y-p2=0,由韦达定理,y1y2=-p2.
y-p2=0,由韦达定理,y1y2=-p2.
当直线PQ的斜率角为90°时,将x=![]() 代入抛物线方程,得y=±p,同样得到
代入抛物线方程,得y=±p,同样得到
y1·y2=-p2.
(2)解:因为光线QN经直线l反射后又射向M点,所以直线MN与直线QN关于直线l对称,设点M(![]() ,4)关于l的对称点为M′(x′,y′),则
,4)关于l的对称点为M′(x′,y′),则
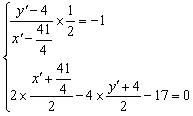 解得
解得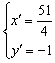
直线QN的方程为y=-1,Q点的纵坐标y2=-1,
由题设P点的纵坐标y1=4,且由(1)知:y1·y2=-p2,则4·(-1)=-p2,
得p=2,故所求抛物线方程为y2=4x.
(3)解:将y=4代入y2=4x,得x=4,故P点坐标为(4,4)
将y=-1代入直线l的方程为2x-4y-17=0,得x=![]() ,
,
故N点坐标为(![]() ,-1)
,-1)
由P、N两点坐标得直线PN的方程为2x+y-12=0,
设M点关于直线NP的对称点M1(x1,y1)
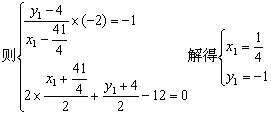
又M1(![]() ,-1)的坐标是抛物线方程y2=4x的解,故抛物线上存在一点(
,-1)的坐标是抛物线方程y2=4x的解,故抛物线上存在一点(![]() ,-1)与点M关于直线PN对称.
,-1)与点M关于直线PN对称.
在解题的过程中,只要注意到各学科知识之间的内在联系,定会有很多巧妙的解题方法.