高中学生学科素质训练

 　 高二数学同步测试期中试题

共150分，考试用时120分钟

一、选择题（本大题共12小题，每小题5分，共60分）

1．已知点（2，－1）和（－3,2）在直线的异侧，则的取值范围是　 （　　）

　　　 A．（4,7）　　　　　　　　B．（－4,7）　　　　　　 C．（－7,4）　　　　　　 D．（－4,4）

2．在下列函数中，当x取正数时，最小值为2的是　　　　  　　　　　　　　　　　　　　　 （　　）

　　　 A．y=x+　 　　　　　　　　　　　　　　　　　　　　 B．　

　　　 C．　　　　　　　 D．y=x²－2x+3

3．如果直线l将圆：x²+y²－2x－4y=0平分，且不过第四象限，那么l的斜率取值范围是（　　）

A．[0，2]　　　　　　　  　　　　　　　　　　B．（0，2）

C．（－∞，0）∪（2，+∞）　　　　　　　D．（－∞，0∪[2，+∞

4．已知定点在直线外，则方程表示　　　　　 （　　）

　　A．与重合的直线　 　　　　　　　　　　　　　 B．与平行的直线　

C．与垂直的直线 　　　　　　　　　　　　　　　　D．点

5．由动点P向圆引两条切线PA、PB，切点分别为A、B，∠APB＝60°，则动点P的轨迹方程是　　　　　　　　　　（　　）

　　　 A．　　　　　B．　　　　　C．　　　　　D．

6．若不等式＞0的解为－3＜x＜－1或x＞2，则a的值为　　　　　　　　　　（　　）

A．2　　　　  　　　B．－2 　　　　　　　　　C．　　　　　　　　　 D．－

7．若点A（4，a）到直线4x－3y－1＝0的距离不大于3，则　　　　　　　　　　　　　　　　 （　　）

　　　 A．－1＜a＜9　　　　　B．0≤a≤10　　　　　　C．5＜a＜8　　　　　　　D．－2≤a≤6

8．不等x－2y+6>0 表示的平面区域在直x－2y+6=0 的　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．右上方　 　　　　 B．右下方　 　　　　 C．左上方　　　　　　D．左下方

9．若=（1，2），=（－2，1）且，分别是直线L₁：ax+(b－a)y－a=0,

 L₂：ax+4by+b=0的方向向量，则a,　b的值分别可以是　　　　　　　　　　　　　　　　 （　　）

　　　 A． 2，1 　　　　　　　 B．1 ，2 　 　　　　 C．－1 ，2　　　　　 D．－2 ，1

10．直线到直线的角为　　　　　　　　　　　　 （ 　 ）

　　　 A．　　　　　　　　 B．　　　　　　　　 C．　　　　　　　　D．

11．过点P（－1，1）作直线l与圆相交于A、B两点，则｜PA｜·｜PB｜等于　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．18　　　　　　　　　　　B．19　　　　　　　　　　　 C．20　　　　　　　　　　　D．21

12．直线 L₁：ax+(1－a)y=3, L₂：(a－1)x+(2a+3)y=2 互相垂直，则a的值为 　　　　 （　　）

　　　 A．－3 　　　　　　　　　 B．1 　　　　　　　　　 C． 0 或－　　　　D．1或－3

二、填空题（本大题共4小题，第小题4分，共16分）

13．已知圆的方程为x²+y²+ax+2y+a²=0，一定点A（1，2），要使过定点A（1，2）作圆的切线有两条，则a的范围是　　　　　　　 

14．过A（1,2）、B（3,0）两点且圆心在直线y=3上的圆的方程是　　　　　　　　　　．

15．已知x ,y满足约束条件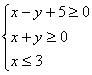则 Z=2x+4y 的最小值是 ____　　　　 ___.

16．一次化学实验中需要用天平称出20g氧化铜粉末, 某同学发现自己所用的天平是不准的(其两臂不等长)，因此, 他采用了下列操作方法：选10g的法码放入左盘, 置氧化铜粉末于右盘使之平衡，取出氧化铜粉末, 然后又将10g法码放于右盘, 置氧化铜粉末于左盘, 平衡后再取出.  他这样称两次得到的氧化铜粉末之和应该　　　　　 20g. (选用“大于”，“小于”，“等于”，“不小于”，或“不大于”填空 )

三、解答题（本大题共6题，共74分）

17．（12分）某商品计划两次提价，有甲、乙、丙三种方案，其中p＞q＞0

次　 　  方案	第一次提价	第二次提价
甲	p%	q%
乙	q%	p%
丙	%	%

经两次提价后，哪种方案的提价幅度大？

18．（本题满分12分）已知过点P（1，4）的直线L在两坐标轴上的截距均为正值，当两截

距之和最小时，求直线L的方程。

19．（本题满分12分）点M（x ，y ）到两定点M₁，M₂距离的比是一个正数M，求点M

的轨迹方程，并说明轨迹是什么图形。

20．（本题满分12分） 已知函数对任意有，

当时，，，求不等式的解集。

　

21．（本题满分12分）解关于的不等式

22．（本题满分14分）已知a , b都是正数，△ABC是平面直角坐标系xOy内, 以两点A ( a , 0 )和B ( 0 , b )为顶点的正三角形，且它的第三个顶点C在第一象限内.

　 （1）若△ABC能含于正方形D = { ( x , y ) 0 £ x £ 1, 0£ y £ 1}内， 试求 变量 a , b 的约束条件，并在直角坐标系aOb内（见答题卷）内画出这个约束等条件表示的平面区域；

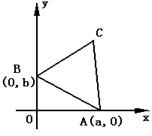　 （2）当( a, b )在（1）所得的约束条件内移动时，求△ABC面积S的最大值，并求此时（a , b ）的值.

期中参考答案

一．选择题 (本大题共12小题, 每小题5分, 共60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	D	A	B	C	B	B	B	A	D	D	D

二．填空题（本大题有4小题, 每小题4分, 共16分）

13．()　 14． 　 15．25 　 16． 　大于　

三、解答题（本大题共6题，共74分）

17．（12分）解：设该商品原价为a，提价后三种方案的价格分别为s，t，u则有：

s=a(1+p%)(1+q%)　t=a(1+q%)(1+p%)　u=a(1+)（1+）　　　　 

显然：s=t=a(1+p%+q%+)，

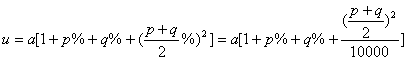
∵()²＞pq，∴u＞s=t　　　　　　　　　　　　　　　　　　　　　　　

故经两次提价后，丙种方案提价幅度最大.

18．（本题满分12分）解：设 L: y－4=k(x－1) , (k<0) L在两轴上的截距分别为a,b.

则a=1－,　b=4－k ,　因为 k<0, －k>0, >0　 

a+b=5+(－k)+ 5+2=5+4=9　。　　　　

当且仅当　－k= 即 k= －2 时 a+b　取得最小值9。

所以，所求的直线方程为y－4=－2(x－1) ,　即 2x+y－6=0　

19．（本题满分12分）

解：设 =2a (a>0) , 以 m₁m₂　所在直线为 x 轴，m₁m₂ 的中垂线为y轴，建立平面坐标系，

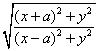依题意　 =m，　　即　 =m,

化为　 (1-m²)x²+2a(1+m²)x+(1-m²)y²+a²(1-m²)=0，

当m=1 时,x=0 ，此时点m 的轨迹为y轴所在直线,

当m1时，(x+a)²+y²=　,此时点m 的轨迹为以 (, 0 ) 为圆

心 ， 为半径的圆 .　　　　

20．（本题满分12分） 解：设且

　　则

　　，

　　即，

　　

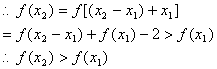
　　故为增函数，

　　又

　　

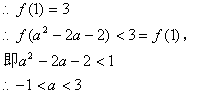
　　因此不等式的解集为。

21．原不等式可化为，于是　　　　　　　　　　　　　　　　．．．2分

当时，原不等式的解集为（1，＋∞）；　　　　　　　　　　　　．．．3分

当时，原不等式可化为

　　∴当时，原不等式的解集为　　　　　　　　　　　　　　　．．．5分

　　　当时，原不等式的解集为　　　　　　　　　　　　　．．．7分

　　　当时，原不等式的解集为　　　　　　　　　　　　　　．．．9分

当时，原不等式可化为，

　　　∴原不等式的解集为　　　　　　　　　　　　．．．12分

22．解: （本题满分14分）（1）顶点C是以A、B为圆心AB为半径的两圆在第一象限的交

点，由圆A: ( x – a)² + y² = a² + b² ,

圆B: x² + ( y – b )² = a² + b² .

解得 x = , y = ，

∴C（， ）　　　　　　　　　　　　 

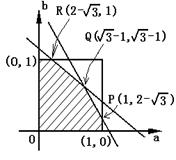△ABC含于正方形D内，即三顶点A，B，C含于区域D内时，

∴ 

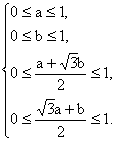
这就是 ( a , b )的约束条件. 其图形为右图的六边形，

∵a > 0 , b > 0 , ∴图中坐标轴上的点除外. 　　　　　　　　　　　　　 

（2）∵△ABC是边长为的正三角形,∴ S = ( a² + b² )

在(1)的条件下, 当S取最大值等价于六边形图形中的点( a, b )到原点的距离最大,

由六边形中P、Q、R相应的OP、OQ、OR的计算.

OP² = OR² = 1² + ( 2 – )² = 8 – 4;

OQ² = 2( – 1)² = 8 – 4.　知:

当 ( a , b ) = ( 1, 2 –), 或(– 1, – 1), 或( 2 –, 1 )时, S_max =2– 3.