2004－2005学年度下学期

高中学生学科素质训练

高二数学期中同步测试题

YCY

本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.

第Ⅰ卷（选择题，共50分）

一、选择题（本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项

　　　 是符合题目要求的）

1．经过空间任意三点作平面　　　　　　　　　　　　　　　　　  　　　　　　　　　 （　　）

　　　 A．只有一个　　　　　　　　　　　　　　　　　　　　　 B．可作二个 　　　　　

　　　 C．可作无数多个　　　　　　　　　　　　　　　　　　D．只有一个或有无数多个

2．若＝（2，1，1）， =（﹣１，x，1）且⊥　，则x的值为　　 　　　　　　（　　）

　　　 A．1　　　　　　　　　　B．－1　　　　　　　　　C．2　　　 　　　　　　D．0

3. 两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm，把它们重叠在一起组成一

　 个新长方体，在这些新长方体中，最长的对角线的长度是　　　　  　　　　　　　　（　　）

　　　 A．　　　　　　　B．　　　　　　　C．　　　　　　　D．

4．已知α，β是平面，m，n是直线.下列命题中不正确的是　　　　　　　 　　 （　　）

　　　A．若m∥n，m⊥α，则n⊥α　　　　　　　 B．若m∥α，α∩β=n，则m∥n

　　　 C．若m⊥α，m⊥β，则α∥β　　　　　　 D．若m⊥α，，则α⊥β

5．在正三棱柱 （　　）

　　　 A．60°　　　　　　　　　 B．90°　　　　　　　　　 C．105°　　　　　　　　 D．75°

6．一个简单多面体的面数为12，顶点数为20，则这个多面体的棱数是　　　　　 （ 　 ）

　　　 A．25　　　 　　　　　B．28　 　　　　　　　　 C．30　 　　　　　　　　 D．32

7．正三棱锥的侧面与底面所成的二面角的余弦值为，则其相邻两侧面所成的二面角的余

　 弦值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　 　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　　 D．0

8．棱柱成为直棱柱的一个必要但不充分条件是　　　　  　　　　　　　　　　 （　  ）

　　　 A．有一条侧棱与底面垂直　　　　　　　　　B．有一条侧棱与底面的两边垂直　

　　　 C．有一个侧面与底面的一条边垂直　　　 D．有两个相邻的侧面是矩形

9．正方形ABCD的边长为6 cm，点E在AD上，且AE＝AD，点F在BC上，且BF ＝BC，

　把正方形沿对角线BD折成直二面角A－BD－C后，则EF ＝　　　　　　　　　　　　　（　  ）

　　　 A．2cm 　　　　　　B．2cm　　　　　 C． 2cm　　　　　　D．6 cm

10．在下列的四个命题中：

①是异面直线，则过分别存在平面，使；

②是异面直线，则过分别存在平面，使；

③是异面直线，若直线与都相交，则也是异面直线；

④是异面直线，则存在平面过且与垂直．真命题的个数为　　　　　　　（　　）

　　　 A．1个　　　　　　　　　　B．2个　　　　　　　　　 C．3个　　　　　　　　 D．4个

第Ⅱ卷（非选择题，共100分）

二、填空题（本大题共4小题，每小题6分，共24分）

11．若AC、BD分别是夹在两个平行平面a 、b 间的两条线段，且AC ＝13，BD＝15，AC、BD在平面b 上的射影长的和是14，则a 、b 间的距离为 　　　　　　  ．

12．二面角内一点到平面和棱的距离之比为，则这个二面角的平

面角是度．

13．在北纬圈上有甲乙两地，它们在纬度圈上的弧长为（为地球的半径），则甲乙两地的球面距离为　　　　　　　　．

14．将边长为2，锐角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，点E、F分别为AC、BD的中点，则下列命题中正确的是　　　　　　 。（将正确的命题序号全填上）

　　①EF∥AB　　　　　　　　　　　　　　　 ②EF是异面直线AC与BD的公垂线

③当四面体ABCD的体积最大时，AC=　④AC垂直于截面BDE

三、解答题（本大题共6题，共76分）

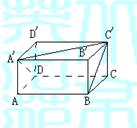
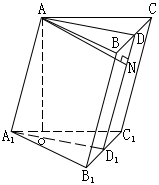
15．（本题满分12分）如图，已知长方体的长宽都是4cm，高为2cm．

　　（1）求BC与，与，与所成角的余弦值；

　　（2）求与BC，与CD，与所成角的大小．

16．（本题满分12分）若平面α内的直角△ABC的斜边AB=20,平面α外一点O到A、B、C三点距离都是25,求：点O到平面的距离．

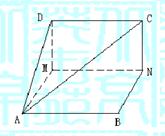
17．（本题满分12分）是边长为1的正方形，分别为上的点，且，沿将正方形折成直二面角

　 （1）求证：平面平面；

　 （2）设，点与平面间的距离为，试用表示．

18．（本题满分12分）已知三棱柱的底面是边长为1的正三角形，，顶点 到底面和侧面的距离相等，求此三棱柱的侧棱长及侧面积．

19．（本题满分14分）正四棱柱ABCD-A₁B₁C₁D₁的底面边长是，侧棱长是3，点E，F分别在BB₁，DD₁上，且AE⊥A₁B，AF⊥A₁D．

①求证：A₁C⊥面AEF；

②求二面角A-EF-B的大小；

③点B₁到面AEF的距离；

④平面AEF延伸将正四棱柱分割成上下两部分，求V_上∶V_下

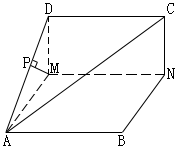
20．（本题满分14分）在直角梯形P₁DCB中，P₁D//CB，CD⊥P₁D，且P₁D=6，BC=3，DC=，A是P₁D的中点，沿AB把平面P₁AB折起到平面PAB的位置，使二面角P—CD—B成45°角.设E、F分别是线段AB、PD的中点.

　 （1）求证：AF//平面PEC；

　 （2）求PC与底面所成角的正弦值.

高二数学期中同步测试题参考答案

一、选择题（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	A	C	B	B	C	D	C	D	A

二、填空题（本大题共4小题，每小题6分，共24分）

11．12　　　　12．90　　　　13．　　  14．②③④

三、解答题（本大题共6题，共76分）

15．(12分) 解：（1）；；　　 （2）90°；90°；0°

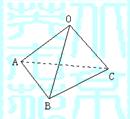
16．(12分) 解：由斜线相等，射影相等知，O在底面的射影为△ABC的外心Q，

又△ABC为Rt△外心在斜边中点，故OQ===

17．(12分) 解：（1）MN⊥AM，MN//CD　∴CD⊥AM

又CD⊥DM ∴CD⊥平面ADM ∴平面ADC⊥平面ADM

(2)∵MN//CD　 MN平面ADC　　 CD平面ADC

∴MN//平面ADC　∴M、N到平面ADC的距离相等

过M作MP⊥AD ∵平面ADM⊥平面ADC ∴MP⊥平面ADC

∵MN⊥DM　 MN⊥AM　∴∠AMN=90⁰

在Rt△ADM中,∴

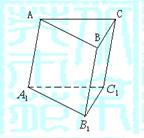
18．(12分) 解：作AO⊥平面A₁B₁C₁，O为垂足

∵∠AA₁B₁=∠AA₁C₁=45⁰ ∴O在∠C₁A₁B₁的平分线上

连结A₁O并延长交B₁C₁于D₁点　∵A₁C₁=A₁B₁　∴A₁D₁⊥B₁C₁

∴A₁A⊥B₁C₁∴BB₁⊥B₁C₁ ∴四边形BB₁C₁C为矩形

取BC中点D，连结AD　DD₁ ∵DD₁//BB₁

∴B₁C₁⊥DD₁又B₁C₁⊥A₁D₁ ∴B₁C₁⊥平面A₁D₁DA

∴平面A₁ADD₁⊥平面B₁C₁CB, 过A作AN⊥DD₁，则AN⊥平面BB₁C₁C

∴AN=AO　　∵四边形AA₁D₁D为□

∴A₁D₁=DD₁　　　　　　　 ∴

19．（14分）解：①∵BC⊥面AA₁B₁B　∴A₁B那么A₁C在平面AA₁B₁B上的射影

又AE⊥A₁B　　AE面AA₁B₁B　 ∴AE⊥A₁C(三垂线定理)

同理：AF⊥A₁D　　又AE，AF面AEF且AE∩AF=A　∴A₁C⊥面AEF

②连AC，BD交于点O，取EF的中点M连OM，AM已知AE=AF=2

BE=DF=1　 ∠OMA即为二面角A—EF—B的平面角

在tan∠AMO=　∴∠AMO=arc tan

③　∴d=

④V_上∶V_下=2∶1

20．(14分) 解法一：设PC中点为G，连FG.∵FG//CD//AE，

且GF=∴AEGF是平行四边形

∴AF//EG，EG平面PEC，∴AF//平面PEC.

（2）连接AC. ∵BA⊥AD，BA⊥AP₁，∴BA⊥AD，BA⊥AP

∴BA⊥平面PAD…①　又CD//BA，∴CD⊥PD，CD⊥AD，

∴∠PDA是二面角P—CD—B的平面角，∴∠PDA=45°.

又PA=AD=3，∴△PAD是等腰直角三角形，∴PA⊥AD……②

由①、②　∴PA⊥平面ABCD，∴AC是PC在底面上的射影.

∵PA=3，，∴，

则，∴PC与底面所成角的正弦值为

解法二：（1）设线段PC的中点为G，连结EG

∵=

∴AF//EG，又EG平面PEC，AF平面PEC，∴AF//平面PEC.

（2）∵BA⊥P₁D，∴BA⊥平面PAD……①又CD//BA，∴CD⊥PD，CD⊥AD，

∴∠PDA是二面角P—CD—B的平面角，∠PDA=45°.又PA=AD=3，∴△PAD是等腰直角三角形，

∴PA⊥AD…②　由①、②　∴PA⊥平面ABCD， 设PA与PC所成的角为

则PC与平面ABCD所成的角为

∵、、两两互相垂直，且

 

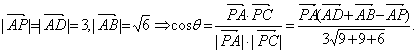
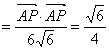
　　　　 故知PC与底面所成角的正弦值为.