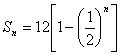新课标人教版高二数学选修1-2练习题
1.下列说法正确的是( )
A、若a>b,c>d,则ac>bd B、若![]() ,则a<b
,则a<b
C、若b>c,则a·b≥a·c D、若a>b,c>d,则a-c>b-d
2.对于任意实数a、b、c、d,命题①![]() ;②
;②![]()
③![]() ;④
;④![]() ;⑤
;⑤![]() .
.
其中真命题的个数是 ( )
(A)1 (B)2 (C)3 (D)4
3.若a,b,c成等比数列,m是a,b的等差中项,n是b,c的等差中项,则![]() ( )
( )
(A)4 (B)3 (C)2 (D)1
4.已知等比数列{an}中,a1+a2=9,a1a2a3=27,则{an}的前n项和 Sn= ________________.
5. 数列1,![]() ,
,![]() ,。。。前100项的和等于( )
,。。。前100项的和等于( )
A
. ![]() B.
B. ![]()
![]()
![]()
6.已知数列{ a n
}满足条件a1 =
–2 , a n + 1 =2 + ![]() , 则a 5 = .
, 则a 5 = .
7.已知数列![]() ,
,![]() ,
,![]() ,则
,则![]()
8.设正数数列![]() 前n项和为
前n项和为![]() ,且存在正数t,使得对所有正整数n有
,且存在正数t,使得对所有正整数n有![]() ,则通过归纳猜测可得到
,则通过归纳猜测可得到![]() =
=
9.数列3,5,9,17,33,…的通项公式![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.当![]() 成等差数列时,有
成等差数列时,有![]() 成等差数列时,有
成等差数列时,有
![]() 成等差数列时,有
成等差数列时,有![]() ,
,
由此归纳:当![]() 成等差数列时有
成等差数列时有![]()
如果![]() 成等比数列,类比上述方法归纳出的等式为
.
成等比数列,类比上述方法归纳出的等式为
.
11.已知f(n+1)=f(n)-![]() (n∈N*)且f(2)=2,则f(101)=______.
(n∈N*)且f(2)=2,则f(101)=______.
12.如果直线l、m与平面α、β、γ满足:![]() ,
,![]() ,
,![]() ,那么必有( )
,那么必有( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
13.复数z对应的点在第二象限,它的模为3,实部是![]() ,则
,则![]() 是( )
是( )
(A)![]() +2i
(B)
+2i
(B)![]() -2i (C)
-2i (C)![]() +2i (D)
+2i (D)![]() -2i
-2i
14.x、y∈R,![]() ,则xy=
,则xy=
15.一同学在电脑中打出如下图若干个圆(○表示空心圆,●表示实心圆)
○●○○●○○○●○○○○●○○○○○●○……
问:到2006个圆中有 个实心圆。
16.如图,它满足①第n行首尾两数均为n,②表中的递推关系类似杨辉三角,则第n行![]() 第2个数是_________.
第2个数是_________.
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5
6 16 25 25 16 6
17. 设有一个直线回归方程为 ![]() ,则变量x 增加一个单位时 ( )
,则变量x 增加一个单位时 ( )
A. y 平均增加 1.5 个单位 B. y 平均增加 2 个单位
C. y 平均减少 1.5 个单位 D. y 平均减少 2 个单位
18.某考察团对全国10大城市进行职工人均平均工资![]() 与居民人均消费
与居民人均消费![]() 进行统计调查,
进行统计调查, ![]() 与
与![]() 具有相关关系,回归方程
具有相关关系,回归方程![]() (单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
(单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( )
(A) 66% (B) 72.3% (C) 67.3% (D) 83%
19.有下列关系:
(1) 名师出高徒; (2) 球的体积与该球的半径之间的关系;(3) 苹果的产量与气候之间的关系;
(4) 森林中的同一种树,其断面直径与高度之间的关系;(5) 学生与他(她)的学号之间的关系;
(6) 乌鸦叫,没好兆; 其中,具有相关关系的是______________
 20.右图给出的是计算
20.右图给出的是计算![]() 的值的一个流程图,其中判断
的值的一个流程图,其中判断
框内应填入的条件是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
21.画一个程序框图,输入一个整数a,判断a是奇数还是偶数.
22.已知f(z)=1+![]() -
-![]() ,且f(-
,且f(-![]() )=10+3i,求复数
)=10+3i,求复数![]() .
.
23.设z1=1+2ai,z2=a-i(a![]() R),已知A={zz-z1≤1},B={zz-z2≤2},A∩B=φ,求a的取值范围
R),已知A={zz-z1≤1},B={zz-z2≤2},A∩B=φ,求a的取值范围
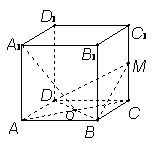 24.如图,在正方体
24.如图,在正方体![]() 中,
中,![]() 为
为![]() 中点,
中点,
![]() ∩
∩![]() 于
于![]() 。求证:
。求证:![]() ⊥平面
⊥平面![]() 。
。
 25.如图
25.如图![]() 是
是![]() 所在平面外一点,
所在平面外一点,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上的点,
上的点,![]() 。求证:
。求证:![]() 。
。
高二数学练习题参考答案:
| 题 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答 | C | A | C |
| A |
|
|
|
| 题 | 9 | 10 | 11 | 12 | 13 | 14 | ||
| 答 | B |
|
| A | B | 5 | ||
| 题 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| 答 | 61 |
| C | D | (1)(3)(4) | A | ||
 21、程序框图如右。
21、程序框图如右。
22、解:f(![]() )=1+z-
)=1+z-![]() f(-z)=1-z+
f(-z)=1-z+![]()
设z=a+bi (a、b∈R) 由f(-z)=10+3i得
1-(a+bi)+a-bi=10+3i
即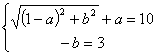 ,解方程组得
,解方程组得![]() ,
,
所以复数z=5-3i
23、解:∵A表示以z1为圆心,1为半径的圆的内部(含边界)
B表示以z2为圆心,2为半径的圆的内部(含边界)
∵A![]() B=φ ∴z1z2>3,∴z1z22>9 ,即(1-a)2+(2a+1)2>9,即 a>1 或 a<-
B=φ ∴z1z2>3,∴z1z22>9 ,即(1-a)2+(2a+1)2>9,即 a>1 或 a<-![]() 。
。
24、证明:连结AB,A1D,在正方形中,A1B=A1D,O是BD中点,∴A1O⊥BD;
连结OM,A1M,A1C1,设AB=a,则AA1=a,MC=![]() a=MC1,OA=OC=
a=MC1,OA=OC=![]() a,AC=
a,AC=![]() a,
a,
∴A1O2=A1A2+AO2=a2+![]() a2=
a2=![]() a2,OM2=OC2+MC2=
a2,OM2=OC2+MC2=![]() a2,A1M2=A1C12+MC12=2a2+
a2,A1M2=A1C12+MC12=2a2+![]() a2=
a2=![]() a2,
a2,
∴A1M2=A1O2+OM2,∴A1O⊥OM,∴AO1⊥平面MBD。
25、证明:取PB的中点![]() ,连结
,连结![]() ,∵
,∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴MQ⊥AB,取
,∴MQ⊥AB,取![]() 的中点
的中点![]() ,连结QD,则QD∥PA,∵
,连结QD,则QD∥PA,∵![]() ∴QD=QB,又
∴QD=QB,又![]() ,∴
,∴![]() ,∴
,∴![]() ,∴AB⊥平面QMN,∴
,∴AB⊥平面QMN,∴![]() 。
。