高二数学期末复习二（直线和圆的方程2）

一、选择题(本大题共10小题，每小题3分，共30分)

1.若命题“曲线C上的点的坐标满足方程f(x,y)=0”是正确的，则下列命题中正确的是

A.方程f(x,y)=0表示的曲线一定是曲线C

B.坐标满足方程f(x,y)=0的点一定在曲线C上

C.方程f(x,y)=0表示的曲线不一定是曲线C

D.曲线C是坐标满足方程f(x,y)=0的点的轨迹

2.直线l将圆x²+y²－2x－4y=0平分，且与直线x+2y=0垂直，则直线l的方程为

A.y=2x　　　　　 B.y=2x－2　 C.y=－x+　　　　　　　 D.y=x+

3.到两个坐标轴距离之差的绝对值等于2的点的轨迹是

A.2条直线　　　　　　B.4条直线　 C.4条射线　　　　　　D.8条射线

4.方程x－1=表示的曲线是

A.一个圆　　　　　　　　　　 B.两个半圆　 C.一个半圆　　　　　D.两个圆

5.方程x²+y²+ax+2ay+2a²+a－1=0表示圆，则a的取值范围是

A.(－∞,－2)　 　　B.(－,2)　  C.(－2,0)　　　D.(－2,)

6.若直线ax+by=1与圆x²+y²=1相交,则点P(a,b)的位置是

A.在圆上　　　　　　　B.在圆外　　C.在圆内　　　　D.都有可能

7.两条曲线y=ax和y=x+a(a>0)有两个不同的公共点，则a的取值范围是

A.a>1　　　　　　B.0<a<1　　 C.　　　　　　　D.0<a<1或a>1

8.圆x²+y²－4x+2y+c=0与直线x=0交于A、B两点,圆心为P,若△PAB是正三角形,则　　 C的值为

A.　　　　　　　　　　 B.－　　 C.　　　　　　D.－

9.与圆x²+y²－4x+2y+4=0关于直线x－y+3=0对称的圆的方程是

A.x²+y²－8x+10y+40=0　　　　　　　　　　　　　　　　　　B.x²+y²－8x+10y+20=0

C.x²+y²+8x－10y+40=0　　　　　　　　　　　　　　　　　　D.x²+y²+8x－10y+20=0

10.曲线y=1+(－2≤x≤2)与直线y=k(x－2)+4有两个交点时，实数k的取值范　围是

A.［，+∞］　　B.(，)　C.(0，)　　　　　 D.(，］

二、填空题(本大题共4小题，每小题4分，共16分)

11.圆心在直线2x－y－7=0上的圆C与y轴交于两点A(0,－4)、B(0,－2),则圆C的方　　程为__________.

12.已知曲线y=kx+1与x²+y²+kx－y－9=0的两个交点关于y轴对称，则k=__________,交点坐标为__________.

13.动圆x²+y²－bmx－2(m－1)y+10m²－2m－24=0的圆心轨迹方程是__________.

14.已知两点M(1，－)、N(－4，),给出下列曲线方程:①2x+y－1=0；②2x－4y+3=0；③x²+y²=3；④(x+3)²+y²=1.

在曲线上存在P点满足PM=PN的所有曲线方程是__________.

参考答案

一、选择题

1 C　2.  A  3.  D　4.  B　5.　D  6.  B　7.  A  8.　A　 9. C　10. B

二、填空题

11.(x－2)²+(y+3)²=5　　　　12.　 0　(±3,1)

13. x－3y－3=0　　　　　  14.　 ②③

三、解答题

15(1)解:要使圆的面积最小，则AB为圆的直径，所以所求圆的方程为　　　　　　　　  (x－2)(x+2)+(y+3)(y+5)=0,即x²+(y+4)²=5.

(2)解法一: 因为k_AB=12,AB中点为(0，－4)，所以AB中垂线方程为y+4=－2x，即2x+y+4=0，解方程组得

所以圆心为(－1，－2).根据两点间的距离公式，得半径r=,因此，所求的圆的方程为(x+1)²+(y+2)²=10.

解法二:所求圆的方程为(x－a)²+(y－b)²=r²，根据已知条件得

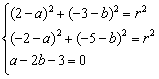
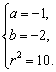
所以所求圆的方程为(x+1)²+(y+2)²=10.

16解:设l与y轴的交点(即反射点)为Q,点P关于y轴的对称点为P′(－1，－1).由光学知识可知直线P′Q为反射线所在的直线，且为圆C的切线.

设P′Q的方程为y+1=k(x+1)，即kx－y+k－1=0,

由于圆心C(4，4)到P′Q的距离等于半径长，

∴=1.解得k=或k=.

由l与P′Q关于y轴对称可得l的斜率为－或－，

∴光线l所在的直线方程为y+1=－(x－1)或y+1=－(x－1),

即4x+3y－1=0或3x+4y+1=0.

17解:∵圆与l₁、l₂相切，故圆心的轨迹在l₁与l₂的夹角平分线上.

∵k₁=－,k₂=2,k₁·k₂=－1,

∴l₁⊥l₂.

设l₁与l₂的夹角平分线为l,其斜率为k,故l与l₂夹角为45°.

∴=1.

∴k=－3或k= (舍去).

l:3x+y－7=0,设圆心(a,b)，则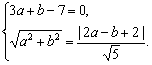

解得或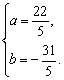

故圆方程为(x－2)²+(y－1)²=5或(x－)²+(y+)²=.

18解:设动点P(x,y)及圆上点B(x₀,y₀).

∵λ==2,

∴

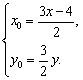
代入圆的方程x²+y²=4

得()²+=4,

即(x－)²+y²=.

∴所求轨迹方程为(x－)²+y²=.

19分析:如下图所示,选择互相垂直的两条对角线所在的直线为坐标轴.本题关键是求出圆心O′的坐标.过O′作AC的垂线,垂足为M,M是AC的中点,垂足M的横坐标与O′的横坐标一致.同理可求出O′的纵坐标.

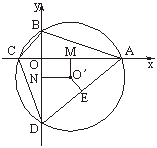
证明:如上图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).

过四边形ABCD外接圆的圆心O′分别作AC、BD、AD的垂线,垂足分别为M、N、E,则M、N、E分别是线段AC、BD、AD的中点,由线段的中点坐标公式,得

x=x_M=,y=y_N=,x_E=,y_E=.

所以O′E==.

又BC=,

所以O′E=BC.