高二数学期末复习一（不等式3）

一、选择题

1.设全集I=R，集合P={x2x²－x＜0}，集合Q={x≤2}，则(　　)

A.P∩ _RQ=φ　 　　　 B.P=_RQ　　 C.P∪Q=R　　　　　　　　　D.P∪Q={xx＞0}

2.x≤2是x+1≤1成立的(　　)

A充分不必要条件　　　　B.必要不充分条件 C.充要条件　 D.既不充分又不必要条件

3.不等式≥2的解集为(　　)

A.［－1,0］　 B.［－1,+∞］  C.(－∞,－1］　　　　　D.(－∞,－1］∪(0,+∞)

4.若关于x的不等式(a²－1)x²－(a－1)x－1＜0对于x∈R成立，则实数a的取值范围是(　　)

A.(－，1]　　　　　　　　 B.［－，1］　 C.(－，1)　　　　　　　　 D.(－∞,－)∪［1,+∞)

5.设A={xx²－2x－3＞0},B={xx²+ax+b≤0}，若A∪B=R，A∩B=(3，4)，则a+b等于(　　)

A.7　　　　 B.－1　　　C.1　　　　　　　　　D.－7

6.设A={xx－1<2},B={x>0},则A∩B等于(　　)

A.{x－1<x<3}　　　 B.{xx<0或x>2}　　C.{x－1<x<0}　　　　　D.{x－1<x<0或2<x<3}

7.若关于x的不等式x+2+x－1＜a的解集是,则a的取值范围是(　　)

A.(3，+∞)　　　　　　B.［3，+∞］　  C.(－∞，3］　　　　　　　 D.(－∞，3)

8.不等式≤0的解集是(　　)

A.{x1≤x＜2} B.{x1＜x＜2或x=－3}　C.{x1≤x＜2或x=－3} D.{x1≤x≤2或x=－3}

9.实数x满足log₃x=1+sinθ,则x－1+x－9的值为(　　)

A.8　　　　 B.－8　　　C.8或－8　　　　　　　　D.与θ有关

10.函数f(x)、g(x)的定义域为R,且f(x)≥0的解集为{x1≤x＜2},g(x)≥0的解集为,则不等式f(x)·g(x)>0的解集为(　　)

A.{x1≤x＜2 }　　　B.R　　 C.　　　　　　　　　　D.{xx<1或x≥2}

二、填空题

11.方程=的解集是__________.

12.建造一个容积为18 m³，深为2 m的长方体无盖水池，如果池底和池壁每平方米的造价分别为200元和150元，那么池的最低造价为__________.

13.设a,a+1,a+2为钝角三角形的三边，则a的取值范围是__________.

14.已知关于x的不等式ax+2<8的解集为(－3,5),则a=__________.

三、解答题

15解不等式(x²+x+1)(x+1)³(x－2)²(3－x)＞0.

16已知函数f(x)=,g(x)=x²－3ax+2a²(a＜0)，若不存在实数x使得f(x)＞1和 g(x)＜0同时成立，试求a的范围.

17已知实数p满足不等式<0,试判断方程u²－2u+5－p²=0有无实根,并给出证明.

18行驶中的汽车，在刹车时由于惯性作用，要继续往前滑行一段距离才能停下，这段距离叫做刹车距离.在某种路面上，某种型号汽车的刹车距离y(m)与汽车的车速x(km/h)满足下列关系:

y=+(n为常数，且n∈N).

我们做过两次刹车试验，有关数据如下图所示，其中

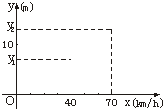
(1)求出n的值；

(2)要使刹车距离不超过18.4 m，则行驶的最大速度应为多少？

19已知不等式(m²+4m－5)x²－4(m－1)x+3>0对一切实数x恒成立,求实数m的取值范围.

20 若不等式组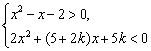的整数解只有－2,k应取何值?

不等式(二)(A卷)

一、选择题

1:A　2:B　3  A　4.　 A  5　 D　　　6　D  7.　 C  8.  C　9　 A　10.   D

二、填空题

11.  {x－1≤x＜2＝ 12　5400元 13　1＜a＜3　 14　－2

三、解答题

15解:∵x²+x+1＞0恒成立，

∴不等式等价于

－1＜x＜2或2＜x＜3.

∴不等式的解集为{x－1＜x＜2或2＜x＜3}.

16解:由f(x)＞1，得＞1,

化简整理得＜0.

解得－2＜x＜－1或2＜x＜3.

即f(x)＞1的解集为A={x－2＜x＜－1或2＜x＜3}.

由g(x)＜0得x²－3ax+2a²＜0,

即(x－a)(x－2a)＜0(a＜0).

则g(x)＜0的解集为B={x2a＜x＜a,a＜0}.

根据题意，有A∩B=.

因此，a≤－2或－1≤2a＜0.

故a的范围是{aa≤－2或－≤a＜0}.

17解:由<0,解得－2<x<－.

∴－2<p<－.

方程u²－2u+5－p²=0的判别式Δ=4(p²－4).

∵－2<p<－,∴<p²<4.∴Δ<0.

由此得出方程u²－2u+5－p²=0无实根.

18解:(1)由图象知，y₁=+=4+n,

y₂=+=n+.

由于5＜y₁＜7,13＜y₂＜15,

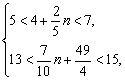∴即

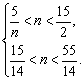
∴＜n＜.

又∵n∈N,∴n=3.

(2)根据题意，得y=+≤18.4.

∴x²+12x－7360≤0,即(x+92)(x－80)≤0.

由于x＞0,∴0＜x≤80,

即行驶的最大速度为80 km/h.

19解:(1)当m²+4m－5=0,即m=1或m=－5时,显然m=1符合题意,m=－5不合题意.

(2)当m²+4m－5≠0时,要使二次不等式对一切x∈R恒成立,

必须

即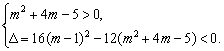

解得1<m<19.

综合(1)(2)得m的取值范围为［1,19).

20 解:由x²－x－2>0,解得x<－1或x>2.

由2x²+(5+2k)x+5k<0化为(2x+5)(x+k)<0.

∵－2是其解,∴k<2.

∴－<x<－k.

∴原不等式组可以化为①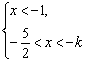或②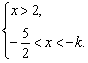

∵k<2,∴－k>－2.

∴①的整数解为－2,而要使②无整数解,只有－k≤3,

即k≥－3.∴－3≤k<2.