钱库第二高级中学数学期末考试试卷2
（时量120分钟 满分100分）
第 I 卷
一. 选择题 (本大题共12小题，每小题3分，共36分. 在每小题给出的四个选项中，只有一项是符合题目要求的.)
1. 若直线x = 1的倾斜角为α ，则α
A. 等于0
B. 等于
C. 等于
D.
不存在
2．双曲线3x2 －y2 ＝3的渐近线方程是
A. y = ±3x
B. y = ±
x
C. y =±
x
D. y = ±
x
3．圆x2 + y2－2 x = 0和 x2 + y2 ＋4y = 0的位置关系是
A. 相离 B. 外切
C. 内切 D. 相交
4. 下列命题中不正确的是
A. 若
B. 若
∥
，
∥，则∥
C. 若
，
，∥，则∥
D. 若一直线上有两点在已知平面外，则直线上所有点在平面外
5. 已知圆C：x2 + y2－2 x－4y－20 = 0，则过原点的直线中，被圆C所截得的最长弦与最短弦的长度之和为
A. 10＋4
B. 10＋2
C. 5＋4
D. 5＋2
6．长轴在x轴上，短半轴长为1，两准线之间的距离最近的椭圆的标准方程是
A. 
B.
C. 
D.
7．已知F1、F2是双曲线16x2 －9y2 ＝144的焦点，P为双曲线上一点，若 PF1PF2 =32,
则∠F1PF2 =
A. 
B.
C. D.
8．已知椭圆的焦点是F1、F2，P是椭圆上的一个动点，如果延长F1P到Q，使得 PQ =
PF2 ，那么动点Q的轨迹是
A. 圆 B. 椭圆
C. 双曲线的一支 D. 抛物线
9. 设椭圆
，双曲线
，抛物线y2 = 2 (m+n) x
(m>n>0 )的离心率分别为e1、e2、e3，则
A. e1e2 > e3 B. e1e2 < e3
C. e1e2 = e3 D. e1e2与e3的大小关系不确定
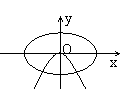10．在同一坐标系中，方程a2
x2 + b2 y2 = 1与a x + b y2 = 0 (a > b
> 0 )的曲线大致是
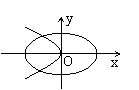
A. B.
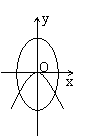
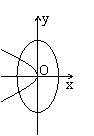
C. D.
11．已知两点A ( –2, 0 ) , B ( 0 , 2 ), 点P是椭圆
=1上任意一点，则点P到直线AB距离的最大值是
A. 
B. 3
.
C. 
D
. 7
12. 对于抛物线 y2 ＝4x上任意一点Q，点P ( a, 0 )都满足 PQ ≥ a ，则a的取值范围是
A. （－∞，0） B. （－∞，2 ]
C. [ 0，2 ] D. （0，2）
钱库第二高级中学数学期末考试答卷
班 学号 姓名
第 I 卷
一. 选择题 （将正确答案的代号填入下表内）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第 II
卷
二. 填空题 (本大题共4小题，每小题4分，共16分. 把答案填
在题中横线上.)
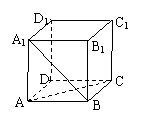
13. 在正方体ABCD-A1B1C1D1中，异面直线A1B和AC所成的
角的大小是 .
14. 已知圆 x2 + y2－6x－7 = 0与抛物线y2 = 2px ( p> 0 ) 的准线
相切，则 p = .
15. 不等式组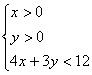
表示的平面区域内的整点（横坐标和纵坐标都是整数的点）
共有 个.
16. 对于椭圆
和双曲线
有下列命题：
①椭圆的焦点恰好是双曲线的顶点;
②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点;
④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是 .
三. 解答题 (本大题共6小题，共48分. 解答应写出文字说明，证明过程或演算步骤.)
17．（本小题满分8分）
已知过点P的直线l绕点P按逆时针方向 旋
转
角﹝0＜＜﹞，得直线为
x－y－2 = 0，若继续按逆时针方向旋转
－角，得直线2x＋y－1 = 0，求直线l的方程.
18.（本小题满分10分）
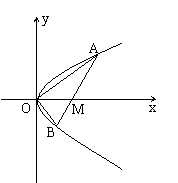如图，已知直线l与抛物线y2 = x相交于A（x1，y1），B（x2，y2）两点，与x轴相交于点M，若y1y2
= －1，
（1）求证：M点的坐标为（1，0）；
（2）求证：OA⊥OB；
（3）求△AOB的面积的最小值.
19．（本小题满分8分）
设F1、F2为椭圆 
的两个焦点，P为椭圆上的一点，已知P、F1、F2是一个直角三角形的三个顶点，且 PF1
> PF2 ，求
的值.
20．（本小题满分8分）
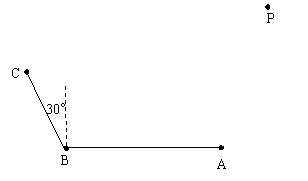
有三个信号监测中心A、B、C，A位于B的正东方向, 相距6千米, C在B的北偏西
，相距4千米. 在A测得一信号，4秒后, B、C才同时测得同一信号，试建立适当的坐标系，确定信号源P的位置. (即求出P的坐标. 设该信号的传播速度为1千米/秒)
21．（本小题满分8分）
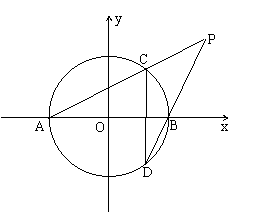
已知A、B是圆x2 + y2 = 1与x轴的两个交点，CD是垂直于AB的动弦，直线AC和DB相交于点P，问是否存在两个定点E、F, 使 PE － PF 为定值？若存在，求出E、F的坐标；若不存在，请说明理由.
22．（本小题满分6分）
已知以坐标原点为中心的椭圆，满足条件
（1）焦点F1的坐标为 ( 3, 0 )；
（2）长半轴长为5.
则可求得此椭圆方程为 
（※）
问可用其他什么条件代替条件（2），使所求得的椭圆方程仍为（※）？
（注：每列出一种正确替代条件，得2分，列出三种正确替代条件，得满分6分. 列出多于三种正确替代条件的，每多一种，另加2分，但本题最高不超过10分，全卷不超过100分.）
湖南师大附中高二年级数学期末考试
参 考 答 案
一、选择题
CBDDA ACABD CB
二、填空题
13. 60° 14. 2 15. 3 16. ① ②
三、解答题
17. 由
得 P ( 1,－1)
据题意，直线l与直线
垂直，故l斜率
∴ 直线l方程为 
即 
.
18. (1 ) 设M点的坐标为（x0, 0）, 直线l方程为 x = my + x0 , 代入y2 = x得
y2－my－x0 = 0 ① y1、y2是此方程的两根,
∴ x0 ＝－y1y2 ＝1，即M点的坐标为（1, 0）.
(2 ) ∵ y1y2 ＝－1
∴ x1x2 + y1y2 = y12y22 +y1y2 ＝y1y2 (y1y2 +1) = 0
∴ OA⊥OB.
（3）由方程①，y1＋y2 = m , y1y2 ＝－1 , 且 OM = x0 =1,
于是S△AOB =
OM y1－y2 =
=
≥1，
∴ 当m = 0时，△AOB的面积取最小值1.
19. 由已知 得 PF1 + PF2 = 6 , F1F2 = 2,
∵△PF1F2为直角三角形，且 PF1 > PF2
∴∠PF2F1为直角或∠F1PF2为直角
(1) 若∠PF2F1为直角， 则 PF1 2 ＝ PF2 2 + F1F2 2,
∴ PF1
2 = (6－ PF1 )2 + 20 
PF1 = 
, PF2 = 
故 
（2）若∠F1PF2为直角， 则 F1F2 2 = PF1 2 + PF2 2
∴20 = PF1 2 + (6－ PF1 )2 PF1 = 4, PF2 = 2,
故 
.
20. 取A、B所在直线为x轴，线段AB的中点O为原点，建立直角坐标系. 则A、B、C的坐标为A ( 3, 0 )、B (－3, 0 )、C (－5, 2
), (长度单位为千米).
由已知 PB － PA = 4, 所以点P在以A、B为焦点，实轴长为4的双曲线的右支上，
其方程为
（x≥2）
①
又B、C同时测得同一信号，即有 PB = PC
∴ 点P又在线段BC的中垂线上，
其方程为
即 
②
由①、②
可得点P的坐标为 ( 8, 5).
21. 由已知得 A (－1, 0 )、B ( 1, 0 ),
设 P ( x, y ), C ( x0, y0 ) , 则 D (x0, －y0 ),
由A、C、P三点共线得 
①
由D、B、P三点共线得 
②
①×② 得 
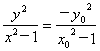③
又 x02 + y02 = 1, ∴ y02 = 1－x02 代入③得 x2－y2 = 1，
即点P在双曲线x2－y2 = 1上， 故由双曲线定义知，存在两个定点E (－
, 0 )、
F (, 0 )（即此双曲线的焦点），使 PE － PF = 2 (即此双曲线的实轴长) 为定值.
22. 用下列任一条件代替（2），都可使所求得的椭圆方程仍为（※）
① 短半轴长为4；
② 离心率 e = 
；
③ 右准线方程为 x = 
；
④ 点P ( 3, 
) 在椭圆上；
⑤ 椭圆上两点间的最大距离为10；
……
（答案是开放的，还可写出多种替换条件.）