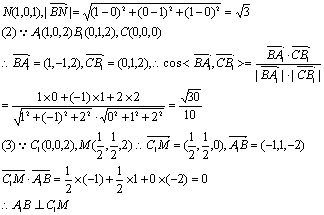高二数学测试题—空间向量
一、选择题:(本大题共10小题,每小题5分,共50分)
1.已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点A、B、C一定共面的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.直三棱柱ABC—A1B1C1中,若![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若向量![]() 、
、![]() ( )
( )
A.![]() B.
B. ![]()
C.![]() D.以上三种情况都可能
D.以上三种情况都可能
4.设向量![]() 是空间一个基底,则一定可以与向量
是空间一个基底,则一定可以与向量![]() 构成空间的另一个基底的向量是 ( )
构成空间的另一个基底的向量是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.对空间任意两个向量![]() 的重要条件是 ( )
的重要条件是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知向量![]() 的夹角为 ( )
的夹角为 ( )
A.0° B.45°
C.90° D.180°
7.设A、B、C、D是空间不共面的四点,且满足![]()
则△BCD是 ( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.不确定
8.已知![]() ( )
( )
A.![]() B.5,2
B.5,2
C.![]() D.-5,-2
D.-5,-2
9.已知![]() ( )
( )
A.-15 B.-5
C.-3 D.-1
10.在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题6分,共24分)
11.若A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线,则m+n= .
12.已知A(0,2,3),B(-2,1,6),C(1,-1,5),若![]() 的坐标为 .
的坐标为 .
13.已知![]() 是空间二向量,若
是空间二向量,若![]() 的夹角为 .
的夹角为 .
14.已知点G是△ABC的重心,O是空间任一点,若![]() 为
为
.
三、解答题(本大题共6题,共76分)
|
|
求证:MN⊥平面PCD.(12分)
17.直三棱柱ABC—A1B1C1中,BC1⊥AB1,BC1⊥A1C
|
|
19.正四棱锥S—ABCD中,所有棱长都是2,P为SA的中点,如图
(1)求二面角B—SC—D的大小;
|
请说明理由(14分)
|
(1)求![]()
(2)求![]()
(3)![]() (14分)
(14分)
高二数学参考答案
空间向量
一、选择题
1.D 2.D 3.B 4.C 5.D 6.C 7.C 8.A 9.A 10.B
二、填空题
11.0 12.(1,1,1)或(-1,-1,-1)
13.![]()
14.3
三、解答题
15.解:


16.证明:

17.证明:

18.解:
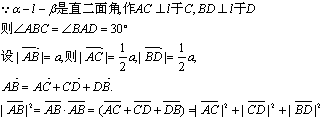
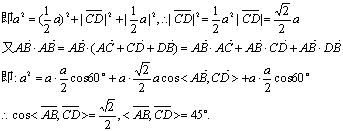
|

20.解:(1)以射线![]() 建立坐标系,则B(0,1,0)
建立坐标系,则B(0,1,0)