2005第二学期温溪高中（高二）期中考试
班级＿＿＿ 学号＿＿＿＿ 姓名＿＿＿＿
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
１．两条异面直线所成角的范围是 （ ）
A．
B.
C.
D.
２．经过空间任意三点作平面（ ）
A．只有一个 B．可作二个
C．可作无数多个 D．只有一个或有无数多个
3 .已知两条不同的直线a、b及平面α，给出四个列命题：
① 若a∥b,b∥α,则a∥α
② 若a⊥α,b⊥α,则a∥b
③ 若a、b与α所成的角相等，则a∥b
④ 若a∥α,b∥α,则a∥b.
其中正确的命题有 （ ）
A、0个 B、1个 C、2个 D、3个
4 .平面M的斜线段AB的长为
A、60º B、30º C、45º D、120º
５ . 在⊿ABC中，AB=AC=5，BC=6，PA⊥平面ABC，PA=8，则P到BC的距离是（ ）
６．在正三棱柱
所
成的角是（ ）
A．60° B．75° C．90° D．105°
７． 正四面体棱长为1，其内切球的表面积为（ ）
A 
π B 
π
C 
π D 
π
８.在边长为
的正三角形ABC中，AD
于D，沿AD折成二面角B-AD-C后，BC=
，这时二面角B-AD-C的大小为 （ ）
A．
B. 
C. 
D. 
９.在棱长为的正方体ABCD-
中，点
到面
的距离为（ ）
A.
B. 
C.
D. 
１０．某单位有7个连在一起的停车位，现有3辆不同型号的车需要停放，如果要求剩余的4个空车位连在一起，则不同的停放方法有 （ ）
A 12种 B 24种 C 60种 D 144种
１１．由0，1，2，3组成比300大的无重复数字的自然数一共有 （ ）
（A）6 （B）18 （C）24 （D）28
１２．在100件产品中，有3件是次品，现从中任意抽取5件，其中至少有2件次品的取法种数为 （ ）
（A）
（B）
（C）
（D）
二、填空题：本大题共４小题，每小题４分，共１６分。
13．二面角
内一点
到平面
和棱
的距离之比为
，则这个二面角的平面角是
度；
14.A、B、C、D四名学生中选出三人参加数理化竞赛，其中A不参加理化竞赛，则不同的参赛方案总数为 ；
15．正三棱锥P－ABC的四个顶点同在一个半径为2的球面上，若正三棱锥的侧棱长为2，则正三棱锥的底面边长是____________.
１６．在正方体的8个顶点中，任取4个点，能连成一个空间四边形的不同取法有 种。
三、解答题（12+12+12+12+13+13=74）
1７（本小题满分12分）6名同学站成一排：
①甲不站排头也不站排尾的不同排法有多少种？
②甲不站排头，且乙不站排尾的不同排法有多少种？
③甲、乙、丙不相邻的不同排法有多少种？
④甲、乙不相邻而且丙、丁也不相邻的排法有多少种?
１８、（12分）有5个男生和3个女生，从中选出5人担任5门不同学科的科代表，求分别符合下列条件的选法数：（1）有女生但人数必须少于男生；(2)某女生一定要担任语文科代表；(3)某男生必须包括在内，但不担任数学科代表；(4)某女生一定要担任语文科代表，某男生必须担任科代表，但不担任数学科代表。
1９、（12分）已知四边形ABCD是矩形，
平面ABCD，N是PB中点，M是AD中点。求证： ⑴MN∥平面PCD；
⑵MN⊥BC；
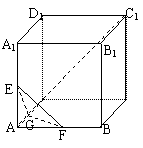
20.（本题12分）如图，正方形ABCD-A1B
分别是AB，AD，AA1的中点,
(1) 求证AC1⊥平面EFG，
(2) 求异面直线EF与CC1所成的角。
 |
D C
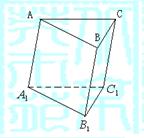
21．（本题满分12分）已知三棱柱
的底面是边长为1的正三角形，
，顶点
到底面
和侧面
的距离相等，求此三棱柱的侧棱长及侧面积．
|
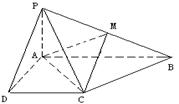
22（1３分）已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，
底面ABCD，且PA=AD=DC=
AB=1，
M是PB的中点。
（1）证明：面PAD⊥面PCD；
（2）求AC与PB所成的角；
（3）求二面角A－MC－B的大小。
