2004－2005学年度下学期

高中学生学科素质训练

高二数学同步测试（4）— 简单几何体

YCY

本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.

第Ⅰ卷（选择题，共50分）

一、选择题：本大题共10个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．一个棱柱为正四棱柱的条件是　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．底面是正方形，有两个侧面垂直于底面　　　

　　　 B．底面是正方形，有两个侧面是矩形

　　　 C．底面是菱形，且有一个顶点处的三条棱两两垂直　　

　　　 D．每个底面是全等的矩形

2．下列命题中正确的一个是　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．四棱柱是平行六面体　　　　　 　　　 B．直平行六面体是长方体

　　　 C．底面是矩形的四棱柱是长方体　 　　　 D．六个面都是矩形的六面体是长方体

3．在底面边长与侧棱长均为a的正三棱柱ABC－A₁B₁C₁中，已知M为A₁B₁的中点，则M

　 到BC的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ 　 ）

　　A．a　　 　　　　B．a　　 　　　　C．a　　　　　　　 D．a

4．若四棱锥的四个侧面与底面所成的角都相等，则其底面四边形必是　　　　　　　　（　　）

A．矩形　　　　　　　B．菱形　　　　　　　 C．圆外切四边形　　 D．圆内接四边形

5．三棱柱的底是边长为4的正三角形, 侧棱长为8，一条侧棱和底面的两边成45°

角，则这三棱柱的侧面面积为　　　　　　　　　　　　　　　　　　　　　　　　（　　）A．32 　　　 B．4（+1） 　　　　　　　　　　　　　　　　C．16（+1） 　　D．32（+1）

6．如图代表未折叠正方体的展开图，将其折叠起来，变成正方体后，图形是　　　　 （ 　 ）

A　　　　　 B　　　　C　　　　  D

7．正三棱锥S－ABC的高SO＝h，斜高SM＝l, 点P在SO上且

分SO所成的比是1 ：2，则过P点且平行于底面的截面面积是　　　　　 　（ 　 ）

　　　 A．(l²－h²) 　　　 B．(l²－h²) 　　 C．(l²－h²)　　　　 D．(l²－h²)

8．将一个边长为a的正方体，切成27个全等的小正方体，则表面积增加了　　　　　 （　　）

　　　 A．　　 　　　　　B．12a²　　　　　　　　　　C．18a²　　　　　　　　　 D．24a²

9．两个平行于圆锥底面的平面将圆锥的高分成相等的三段，那么圆锥被分成的三部

　 分的体积的比是　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 （　　）

A．1∶2∶3　　　　　 B．1∶7∶19　　　　 C．3∶4∶5　　 　　 D．1∶9∶27

10．设正多面体的每个面都是正n边形，以每个顶点为端点的棱有m条，棱数是E，面数是

　　F，则它们之间的关系不正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．nF=2E　　　　　　　 B．mV=2E　 　　　　　C．V+F=E+2　　　　　　D．mF=2E

第Ⅱ卷（非选择题，共100分）

二、填空题：本大题满分24分，每小题6分，各题只要求直接写出结果．

11．长方体高为ｈ，底面积为Ｑ，垂直于底面的对角面面积为Ｍ，则长方体的全面积为　　．

12．直三棱柱ABC－A₁B₁C₁的体积为V，P、Q分别是侧棱AA₁与CC₁上的点，且AP=C₁Q，则四棱锥B－APQC的体积=　　　　　  　　　 ．

13．已知正四棱锥S－ABCD的侧面与底面所成的角为60°，过边BC的截面垂直于平面ASD，交平面ASD于EF，则二面角S－BC－E的平面角为　　　　　　 ．

14．矩形ABCD的边长分别为a，b(a<2b)，

E是DC的中点，把矩形沿AE、BE折成

一个三棱锥的三个侧面(C、D重合)，则

最大的侧面与底面所成的二面角的正弦

值是　　　　　 ．

三、解答题：本大题满分76分．

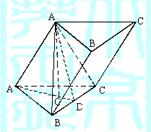
15．（12分）在棱锥P—ABC中，PA、PB、PC两两成60°角，PA=a，PB=b，PC=c，求三

　　　棱锥P—ABC的体积.

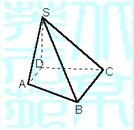
16．（12分）如图，在四棱锥P－ABCD中，底面ABCD是边长为1的菱形，ÐABC＝60°，

PC⊥平面ABCD，PC＝1，E为PA的中点．

　 （1）求证：平面EDB⊥平面ABCD；

　 （2）求二面角A－EB－D的正切值；

　 （3）求点E到平面PBC的距离．

17．（12分）正三棱柱ABC—A₁B₁C₁中，AA₁=2AB，D、E分别是侧棱BB₁、CC₁上的点，

　　且EC=BC=2BD，过A、D、E作一截面，求：

　 （1）截面与底面所成的角；

　 （2）截面将三棱柱分成两部分的体积之比.

18．（12分）C₇₀ 分子是与C₆₀分子类似的球状多面体结构，它有70个顶点，以每个顶点为一端都有3条棱，各面都是五边形或六边形。求C₇₀分子中五边形和六边形的个数．

19．（14分）斜三棱柱ABC-A₁B₁C₁的底面是边长为2的正三角形，顶点A₁在底面的射影O

是△ABC的中心，异面直线AB与CC₁所成的角为45°.

　 （1）求证：AA₁⊥平面A₁BC；

　 （2）求二面角A₁－BC—A的平面角的正弦值；

　 （3）求这个斜三棱柱的体积.

20．（14分）如图，四棱锥的底面是直角梯形，已知垂直底面，

　　且，．

　 （1）求证：平面平面；

　 （2）若为侧棱上的一点，当为何值时，

平面，证明你的结论；

　 （3）若，求二面角的大小．

　　

参考答案（四）

一、选择题（本大题共10小题，每小题5分，共50分）

题　号	1	2	3	4	5	6	7	8	9	10
答　案	C	D	A	C	D	B	A	B	B	D

二、填空题（本大题共4小题，每小题6分，共24分）

11．　　  12．　　　　 13．30°　　　　 14．

三、解答题（本大题共6题，共76分）

15．(12分) 解：如图，设顶点A在平面PBC上的射影

　　为O，连结PO，由题知PA、PB、PC两两成60°角，

　　∴PO是∠BPC的平分线，在平面PBC上，过O作OE⊥PB，

　　连结AE，则AE⊥PB

16．(12分) (1) 证明：连结AC交BD于O，连EO　　 ∵ O是AC中点，E是PA中点

　　　　 ∴ EO∥PC　　　　　　　　　　　∵ PC⊥平面ABCD，∴ PC⊥AO，PC⊥BO 　　 ∴ EO⊥AO，EO⊥BO　

∴ 　EO⊥平面ABCD　　 ∵ EO Ì 平面EDB　　　　∴ 平面EDB⊥平面ABCD．

(2)　　 解：∵ 平面EDB⊥平面ABCD，交线为BD，又AO⊥BD　　　　　　　　　　　　　∴ AO⊥平面EDB

　　　　 过O作OM⊥BE于M，连AM，则AM⊥BE∴ ÐAMO为二面角A－BE－D的平面角

　　 在Rt△EOB中，OB＝，EO＝PC＝　　　　

∴ EB＝1　　　　　　　　　　　 ∵ BE×OM＝OE×OB 　　　　　　　　　　　　　　　　　　

∴ OM＝＝ 　∵ 在Rt△AOM中，OA＝　　　　　　　　　　

∴ tan ÐAMO＝ ＝ ．

(3)　　 解：∵ EO∥PC，PC Ì平面PBC，∴ EO∥平面PBC　　　　　　　　　　　　　　　　 ∴ E到平面PBC的距离就是O到平面PBC的距离
　　　　

∵ 平面PBC⊥平面ABCD交线为BC，过O作OF⊥BC于F　　　　　　　　　　

∴ OF⊥平面PBC，OF即为所求　　　　　　　　　　　　　

　　　　 ∵ 菱形ABCD中，ÐABC＝60°　　　　　　　　　　　　　　　

　　　　 ∴ OF＝OB·sin ÐOBF＝×＝

　　　　 即点E到平面PBC的距离为 ．

17．(12分) 解（1）延长ED交CB延长线于F，

为截面与底面所成二面角的平面角.　在Rt△AEC中，EC=AC，故得∠EAC=45°.

（2）设AB=a，则，

.

18．(12分) 解：设有x个五边形和有y个六边形，则F=x+y,V=70,E=

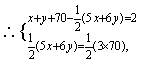
　  答：略。

19．（14分）由已知可得A₁-ABC为正三棱锥，∠A₁AB=45°

　　　　 ∴∠AA₁B=∠AA₁C=90°即AA₁⊥A₁B,AA₁⊥A₁C

　　　　 ∴AA₁⊥平面A₁BC

（1）连AO并延长交BC于D,则AD⊥BC，连A₁D,

则∠ADA₁为所求的角.由已知可得 AD＝Absin60°＝,

AA₁=Absin45°=,∴sin∠ADA₁=

（2）在Rt△AA₁D中，A₁D=∴A₁O=

　　　　 ∴V_柱＝S_△ABC·A₁O=·4·sin60°·.

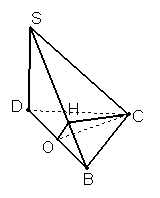
20．(14分) 证明：（１）平面ABCD，.又，

　　　　 故平面SCD，平面SBC，故平面SBC平面SCD.

（2）时，AE//平面SCD.

法一：取SB的中点E，BC的中点F，连结AF，则AF//CD，EF//SC.

　　　　 故EF//平面SCD，AF//平面SCD；平面AEF//平面SCD.

　　　　 而AE平面AEF，AE//平面SCD

法二：取SB、SC的中点分别为E、G，连结EG、DG.则GE//BC，GE=BC，

　　　　 又AD//BC，AD=BC，故AD//GE且AD=GE.

　　　　 于是四边形AEGD为平行四边形。故AE//DG，又DG平面SCD，

　　　　 故AE//平面SCD.

（3）作COBD于O，又SD平面BCD，故SDCO，

　　　　 从而CO平面SBD　，作CHSB于H，

　　　　 连结OH，则OH为CH在平面SBD上的射影，

　　　　 故OHSB，CHO为二面角C－ＳＢ－Ｄ的平面角.

设AD=a，则BC=CD=2a　　于是SA=AB=a ，

　　　　 故SD==2a　 则 CO=a

　　　　 则CH=

　　　　 而sinCHO

故CHO　　　　　二面角C－SB－D为

另解：……三角形SBO是三角形SBC在平面SBD上的射影.

　　　　 设二面角C－SB－D的平面角为

　　　　 则cos=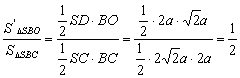,故=