钱库第二高级中学数学期末考试试卷7
班次 ____ 姓名 _____ 计分
一.选择题:(本大题共14小题;每小题3分,共42分)
1、若a,b,c∈R,且a>b,则下列不等式中一定成立的是( )
A.ac>bc B. ac2>bc2 C. a2>b2 D. c-b>c-a
2、过两点P(m,2m+2),Q(1,4)的直线与直线2x-y-3=0平行,则m的值是( )
A. m=1 B. m= -1 C. m≠1 D. m≠ -1
3、直线![]() 与
与![]() 的斜率是方程6x2+x-1=0的两个实数根,则直线
的斜率是方程6x2+x-1=0的两个实数根,则直线![]() 与
与![]() 的夹角是( )
的夹角是( )
A. 45° B. 60° C. 30° D. 90°
4、若直线方程是y = xsin+ 3 , 则直线的倾斜角是( )
A、 300 ; B、450 ; C、600 ; D、 900。
5、圆心在抛物线![]() 上,且与
上,且与![]() 轴和该抛物线的准线都相切的圆的方程是( )
轴和该抛物线的准线都相切的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6、![]() 是方程
是方程 ![]() 表示椭圆或双曲线的
( )
表示椭圆或双曲线的
( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分不必要条件
7、圆C切![]() 轴于点M且过抛物线
轴于点M且过抛物线![]() 与
与![]() 轴的两个交点,O为原点,则OM的长是 ( )
轴的两个交点,O为原点,则OM的长是 ( )
A.4 B.![]() C.
C.![]() D.2
D.2
8、与曲线![]() 共焦点,而与曲线
共焦点,而与曲线![]() 共渐近线的双曲线方程为( )
共渐近线的双曲线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、若抛物线![]() 与圆
与圆![]() 有且只有三个公共点,则
有且只有三个公共点,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、抛物线![]() 上有一点P,P到椭圆
上有一点P,P到椭圆![]() 的左顶点的距离的最小值为( )
的左顶点的距离的最小值为( )
A.![]() B.2+
B.2+![]() C.
C.![]() D.
D.![]()
11、方程![]() 与
与![]() 的曲线在同一坐标系中的示意图应是
( )
的曲线在同一坐标系中的示意图应是
( )

12、若椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点F1、F2,P是两曲线的一个交点,则
有相同的焦点F1、F2,P是两曲线的一个交点,则![]() 的面积是 ( )
的面积是 ( )
A.4 B.2 C.1 D.![]()
13、一个圆的圆心为椭圆的右焦点,且该圆过椭圆的中心交椭圆于P,直线PF![]() (F
(F![]() 为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14、若动点A(x1, y1),B(x2, y2)分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB中点M到原点距离的最小值为( )
A.3![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
二、填空题:(每小题4分,共16分)
15、不等式 –x2 +ax +6a2 > 0 (a < 0) 的解集是____________________
16、过点B(2,3)且在两坐标轴上有相等截距的直线方程是________________
17、已知双曲线的两条渐近线方程是2x![]() 3y=0,实轴长为12,则双曲线的方程为________
3y=0,实轴长为12,则双曲线的方程为________
18、椭圆![]() 关于抛物线y2 = -4x的准线l对称的椭圆方程是________
关于抛物线y2 = -4x的准线l对称的椭圆方程是________
三、解答题:(本大题共6小题,共42分,要求写出必要的解答过程,否则不能得分)
19、(本题满分7分)已知直线l在y轴上的截距为-3,且它与两坐标轴围成的三角形的面积为6,求直线l的方程.
20、(本题满分7分)已知圆心在直线x-y-4=0上,且与直线
![]() 圆的方程.
圆的方程.
21、(本题满分7分)已知椭圆中心在原点,焦点在x轴上,离心率![]() ,它与直线x+y+1=0的交点为P、Q,且以PQ为直径的圆过原点,求椭圆方程。
,它与直线x+y+1=0的交点为P、Q,且以PQ为直径的圆过原点,求椭圆方程。
22、(本小题满分7分)双曲线![]() 的右支上存在与右焦点和左准线等距离的点,求离心率
的右支上存在与右焦点和左准线等距离的点,求离心率![]() 的取值范围.
的取值范围.
23、(本小题满分7分)已知圆![]() 和抛物线
和抛物线![]() 上三个不同的点A、B、C,如果直线AB和AC都与圆O相切,求证:直线BC也与圆O相切。
上三个不同的点A、B、C,如果直线AB和AC都与圆O相切,求证:直线BC也与圆O相切。
24、(本小题满分7分)已知椭圆的一个顶点为A(0,-1),焦点在x轴上,若右焦点到直线![]() 的距离为3。(1)求椭圆的方程; (2)设椭圆与直线
的距离为3。(1)求椭圆的方程; (2)设椭圆与直线![]() 相交于不同的两点M、N,.当
相交于不同的两点M、N,.当![]() 时,求m的取值范围。
时,求m的取值范围。
答案:DCABD BDADA ACDA
15、3a<x<-2a;
16、x + y = 5, y = x;
17、--= 1或 --= 1;
18、+ = 1;
19、3x –4y –12=0 或3x+4y+12=0;
20、因为交点坐标到圆点距离为1,所以圆心在直线 y= -x上,故可求出圆心坐标(2,-2),易求圆的方程为 (x-2)2 + (y+2)2 = 9
21、设椭圆方程为 + = 1,以直线方程x+y+1=0代入得(a2+b2)x2 +2a2x+a2—a2b2=0,
设P(x1,y1),Q(x2,y2),∴x1+x2= , x1x2=, ∵OP ⊥ OQ, ∴= --1, y1y2=-x1x2, ∴ 2a2b2=a2+b2, ∵= , ∴a2 = ,b2 = 。
22、设M![]() 是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离
是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离![]() ,即
,即![]() ,由双曲线定义可知
,由双曲线定义可知  ……4分
……4分
由焦点半径公式得 ![]()
![]() …………………………6分
…………………………6分
而![]() 即
即 ![]() 解得
解得![]() 但
但 ![]() ……………………………………9分
……………………………………9分
23. 设![]() ,
,![]() 则
则
AB的方程为 ![]()
BC的方程为 ![]()
AC的方程为 ![]() ……………………………………3分
……………………………………3分
![]() 为圆的切线,有
为圆的切线,有 即
即![]()
同理![]() 、
、![]() 为方程
为方程![]() 的两根,则
的两根,则 ![]() ……………………8分
……………………8分
于是圆心到直线BC的距离 故BC与圆O
故BC与圆O
相切。…………………………………………10分
24、(1)依题意可设椭圆方程为 ![]() ,则右焦点F(
,则右焦点F(![]() )由题设
)由题设
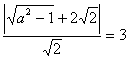 解得
解得![]() 故所求椭圆的方程为
故所求椭圆的方程为![]() .
.
![]() ………………………………………………3分.
………………………………………………3分.
(2)设P为弦MN的中点,由 得
得 ![]()
由于直线与椭圆有两个交点,![]() 即
即 ![]() ①………………5分
①………………5分
![]() 从而
从而![]()
![]() 又
又![]() ,则
,则
![]() 即
即 ![]() ②…………………………7分
②…………………………7分
把②代入①得 ![]() 解得
解得 ![]() 由②得
由②得 ![]() 解得
解得![]() .故所求m的取范围是 (
.故所求m的取范围是 (![]() )……………………………………9分
)……………………………………9分