高 二 数 学（复习二）
（第Ⅰ卷 选择题部分）
一、选择题：（本大题每小题5分，共60分．在每小题给出的四个选项中,只有一项是符合要求的）
1.已知点A（1，2）、B（3，1），则线段AB的垂直平分线的方程是( )
(A)
(B)
(C)
(D)
2.过两点
和
的直线在
轴上的截距是( )
(A)
(B) 
(C) 
(D) 2
3.直线x – 2y +2 = 0与直线3x – y + 7 = 0的夹角等于 ( )
(A) 
(B)
(C) 
(D) arctan7.
4．若直线l1：ax+(1－a)y=3，与l2：（a－1）x+(2a+3)y=2互相垂直，则a的值为（ ）
(A) －3
(B) 1
(C) 0或－
( D) 1或－3
5.不等式
的解集是( )
（A）
（B）
（C）
（D）
6.过点A(-2，m)和B(m，4)的直线与直线2x+y-1=0平行，则m的值为（ ）
（A）0 （B）-8 （C）2 （D）10
7.点P（2，5）关于直线x+y=1的对称点的坐标是( )
(A)（－4，－1） (B)（－5，－2） (C)（－6，－3） (D)（－4，－2）
8.下列结论正确的是( )
(A)当
(B)
(C)
的最小值为2 (D)当
无最大值
9.设
分别表示同一直线的横截距,纵截距,斜率和原点到直线的距离,则有( )
(A) 
(B) 
(C)
(D) 
10.在直角坐标系中，满足不等式 x２－y2≥0 的点（x，y）的集合（用阴影部分来表示）的是( )
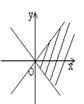
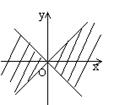
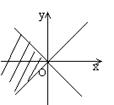
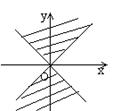
(A) (B) (C) (D)
11.已知点P（x，y）在不等式组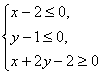
表示的平面区域上运动，则z＝x－y的取值范围是 （ ）
(A) [－2，－1] (B) [－2，1] (C) [－1，2] (D) [1，2]
12.若动点A（x1,y1），B（x2,y2）分别在直线l1：x+y－7=0和l2：x+y－5=0上移动，则AB中点M到原点距离的最小值为（ ）
(A) 3
(B) 2
(C) 3
(D) 4
（第Ⅱ卷 非选择部分）
二、填空题：（本大题每小题4分，共24分．把答案填在题中横线上）
13、经过点M（－2，－3）在x轴，y轴上截距相等的直线方程是____________.
14.直线
与两坐标轴围成三角形的面积是，则t的值是________.
15．函数
(x＞－1)的最小值是
.
16.方程
=
的解集是 _____________.
17.直线
过点
,
过点
,若
,且
之间的距离最大,此时方程是____________
18.下列命题正确的序号为___________
①.和x轴平行的直线，它的倾斜角为0°.
②两条直线垂直的充分条件是它们斜率之积为-1
③直线的斜率为
,则直线的倾斜角为
④不经过原点的直线都可以用方程
表示
⑤当
且
时,直线
和直线
平行.
三、解答题：(本大题共5小题，共66分，解答应写出文字说明、证明过程或演算步骤．)
19. (本小题满分12分)
已知
, B = x + 1, 当x ≠ 1时，试比较A与B的大小, 并说明理由.
20.(本小题满分12分)如图,已知
,直线
和直线
交于点
,交
轴于点
.
(1)求
角平分线所在直线方程;
(2)求
的面积.
21. (本小题满分14分)正方形中心为G（-1，0），一边所在直线的斜率为3，且此正方形的面积为
，求此正方形各边所在的直线方程。
22.(本小题满分14分)电视台为某个广告公司特约播放甲乙两套专题片.其中专题片甲播放时间为20分钟,广告时间为1分钟,收视观众为60万.专题片乙播放时间为10分钟,广告时间为1分钟,收视观众为20万.广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供86分钟的节目时间.问:电视台每周应播映甲乙两套专题片多少次,才能获得最高的收视率?
23.(本小题满分14分)已知过点
且斜率为
的直线
和
轴分别交于
,过作直线
的垂线,垂足分别为
.问
多大时四边形
的面积最小?并求出其最小值.
 |
参考答案
一.选择题 BABDB BABAB CA
二.填空题 (13). 
(14).
(15). 9
(16). （－1，0）∪[3，+∞] (17). 5x-y-18=0 (18).①②
三.解答题
19.解 
A – B = 
=
，(3分)
由
> 0得x
< – 1或1 < x < 2
(3分)
∴ 当x < – 1或1 < x < 2时, A > B； 当 – 1< x < 1或x > 2时, A < B；
当x = – 1或x = 2时, A = B． (6分)
20.(1)由
得
又
(2分)
∴
(2分)
设的平分线交
于
,直线
的斜率为
∴
∴
(3分)
即所求的方程是
(2分)
(2)设C到直线AB的距离为
∴
又
∴
(3分)
21解：∵正方形的面积为14.4 ∴正方形的边长为
(1分)
∵正方形的一边所在直线的斜率为3
∴可设该边所在直线的方程为y=3x+m (2分)
依题意得：
∴m=9或m= -3 (3分)
∴正方形的两边所在直线的方程为：y=3x+9和y=3x-3 (2分)
又知正方形的另两边所在直线的斜率为
可设为y=x+n 即x+3y-3n=0 (3分)
∴
∴n=
或n=
∴正方形的另两边所在直线的方程为：x+3y-5=0和x+3y+7=0 (3分)
22.设每周甲播映次.乙播映次.则有 (1分)
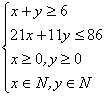(4分)
要使收视率最高,只要
最大 (2分) (图形3分)
由图可知:当
时 
(3分)
答: 每周甲播映4次.乙播映2次才能获得最高的收视率. (1分)
23.解:设的方程为
.则
(2分)
PR的方程为:
(1分)
QS的方程为:
(1分)
因为PR//QS
所以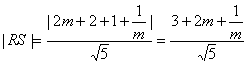
(2分)
又
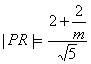
(2分)
四边形PRSQ为梯形
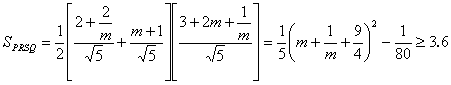(4分)
当且仅当
时取等号,此时S的最小值是3.6. (2分)