高二期中考理科数学试题　

一、选择题（每小题5分，本题满分60分）

1. 直线 l₁⊥l₂ 是 k₁·k₂=－1 的

（A）充分而不必要条件　　　（B）必要而不充分条件

（C）充要条件 　　　　　　 （D）既不充分也不必要条件

2. 设F₁、F₂为定点，F₁F₂=6，动点M满足MF₁+MF₂=6，则动点M的轨迹是

（A）一个椭圆　　（B）两个圆　　（C）一条直线　　（D）一条线段

3. 双曲线的离心率为

（A）　　　 （B）2　　　　 （C）　　　 （D）

4. 已知点到直线的距离等于，且，则

值等于

(A)　　 (B)　　  (C)　　 (D)　　　　　　　　　　　　　　  　

5.圆：和：的位置关系是

(A)外切　　　　(B)内切　　  (C)相交　　　 (D)相离

6. 椭圆的焦点坐标是

　　（A）(,0)　　（B）(0, )　　 （C）(,0)　 （D）(0, )

7.双曲线=1右支上一点P到右焦点距离为2，则P到左准线的距离为

(A)12　　　　(B)10　　　　　  (C) 8　　　　　 (D)6翰林汇

8. 设k＞1，则关于x、y的方程（1-k）x²+y²=k²-1所表示的曲线是

（A）长轴在x轴上的椭圆　　　　　　 （B）长轴在y轴上的椭圆

（C）实轴在x轴上的双曲线　　　（D）实轴在y轴上的双曲线

9．已知椭圆，F₁,F₂是它的焦点，AB是过F₁的弦，则ABF₂的周长为

　　　(A)　　　　　　　　 (B)　　　　　　　　　　(C)　　　　　　　　　　　 (D)

10. 若点到点的距离之和最小，则的值为　　

　 （A）－2　　　　（B）－1　　　　（C）2　　　　（D）1

11．若椭圆(m>n>0)与双曲线(s>0, t>0)有相同的焦点F₁和F₂(m≠s)，P是两曲线的一个公共点，则PF₁·PF₂的值是　　　

　（A）　　 （B）m－s　　　 （C） 　　 （D）

12. 不等式组 表示的平面区域是 

　 （A）　　　　　　 （B）　　　　　　  （C）　　　　　　 （D）

 

二、填空题（每小题4分，本题满分16分）

13．若实数x, y满足(x－2)²+y²=1，则的取值范围是　　　　　　　　  ．

14. 曲线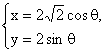（θ为参数）的普通方程是　　　　　　　　　　　 . ；

15.　点P是双曲线x²－y²=2上的动点，F是它的右焦点，则线段PF的中点M的轨迹方程______________。

16. 2003年10月，我国首次载人航天飞行获得圆满成功。“神舟”升空，巨龙腾飞，一个伟大的东方民族的发展进程，从此跃上了一个新的起点。“神舟五号”飞船变轨前的运行轨道是以地心为一个焦点的椭圆，飞船近地点、远地点离地面的距离分别200公里、350公里，设地球半径为R公里，则飞船轨道的离心率为为___________________.

17. 求以椭圆＋=1的右焦点为圆心，且与双曲线－=1的渐近线相切的圆的方程.

18. 光线由点P（1，2）射到直线l:x+y+1=0上，反射后经过点Q（1，－1），求入射光线所在的直线方程.

19.已知圆的方程x²＋y²＝25，点A为该圆上的动点，AB与x轴垂直，B为垂足，点P分有向线段BA的比λ=．

（1） 求点P的轨迹方程并化为标准方程形式；

（2） 写出轨迹的焦点坐标和准线方程．

20. 如图，AB为半圆的直径，P为半圆上一点，AB=10，∠PAB=α，且sinα=，建立适当的坐标系，求A、B为焦点且过P点的椭圆的方程.

21. 若点A、B分别是椭圆的右顶点和上顶点，在椭圆的第一象限内的图象上求一点P，使ΔABP的面积最大，并求ΔABP面积的最大值.

22. 已知双曲线C的顶点与焦点分别是椭圆=1的焦点与顶点，若F₁、F₂是双曲线C的左、右焦点，点P在双曲线C上，且PF₁·PF₂=32.，求∠F₁PF₂的大小.

高二上理科A期中考数学参考答案

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	D	A	A	B	C	C	D	D	A	B	C

13. [－, ] .　  14.　 15. 2(x－1)²－y²=1 .　 16.  .

17. 解： ∵a ²= 169，b²=144,　∴c ² = 25　 ∴c = 5

∴右焦点为F（5，0）即圆心为（5，0）

　　　　又双曲线的渐近线为± ＝0　　∴圆的切线方程为4x+3y=0　

　　　　设圆的半径为r，则r == 4　　∴圆的方程为（x －5）²＋ y ² ＝16　

18.解：设点Q关于l的对称点为Q’(x,y),则

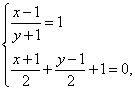　 　　求得x=0,y=-2;即Q’（0，-2）.

∴直线PQ’的方程为y=4x-2,即4x-y-2=0.

根据光反射的性质，入射线所在的直线方程为4x-y-2=0.

19.解：（1）设点P(x, y)是轨迹上任意一点，点A的坐标是(x₁, y₁), 点B的坐标是(x₁, 0),

　∵点P分有向线段BA的比λ＝,

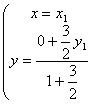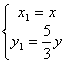　∴ , ∴ ,　又点A在圆x²＋y²＝25上，

　∴ x²＋y²＝25, 即 (y≠0)，

 （2） 椭圆的焦点坐标是(－4, 0), (4, 0), 准线方程是x＝±

20.解：以AB所在直线为x轴，以AB的中垂线为y轴，建立平面直角坐标系。

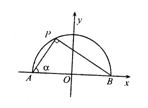由AB=10，得A（-5，0），B（5，0），连结PB.

∵P在半圆上，∴PA⊥PB.

Rt△PAB中，sinα=，∴PB=ABsinα=8，PA==6.

设以A、B为焦点，且过点P的椭圆方程为=1（a＞b＞0）

则2a=PA+PB=14，2c=10， ∴a=7，c=5，b²=24.

∴所求椭圆方程为=1.

21.解：依题意，直线AB的方程是即2x+3y-6=0.设则P点到直线AB的距离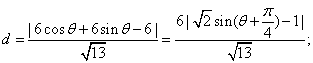

；

点P的坐标为

22. 解：由题意知：双曲线C的方程为=1

设PF₁=m，PF₂=n，∠F₁PF₂=θ，则F₁（-5，0），F₂（5，0）.

∴PF₁-PF₂=m-n=6，m·n=32，F₁F₂=10，

ΔPF₁F₂中，由余弦定理得：

10²=m²+n²-2mncosθ

又m²+n²=（m-n）²+2mn

∴（m-n）²+2mn（1-cosθ）=100

∴cosθ=0　　　∵0＜θ＜π

∴θ=，即∠F₁PF₂=.

高二上理科A期中考数学参考答案

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	D	A	A	B	C	C	D	D	A	B	C

13. [－, ] .　  14.　 15. 2(x－1)²－y²=1 .　 16.  .

17. 解： ∵a ²= 169，b²=144,　∴c ² = 25　 ∴c = 5

∴右焦点为F（5，0）即圆心为（5，0）

　　　　又双曲线的渐近线为± ＝0　　∴圆的切线方程为4x+3y=0　

　　　　设圆的半径为r，则r == 4　　∴圆的方程为（x －5）²＋ y ² ＝16　

18.解：设点Q关于l的对称点为Q’(x,y),则

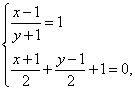　　　 求得x=0,y=-2;即Q’（0，-2）.

∴直线PQ’的方程为y=4x-2,即4x-y-2=0.

根据光反射的性质，入射线所在的直线方程为4x-y-2=0.

19.解：（1）设点P(x, y)是轨迹上任意一点，点A的坐标是(x₁, y₁), 点B的坐标是(x₁, 0),

　∵点P分有向线段BA的比λ＝,

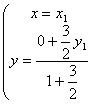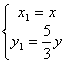　∴ , ∴ ,　又点A在圆x²＋y²＝25上，

　∴ x²＋y²＝25, 即 (y≠0)，

 （2） 椭圆的焦点坐标是(－4, 0), (4, 0), 准线方程是x＝±

20.解：以AB所在直线为x轴，以AB的中垂线为y轴，建立平面直角坐标系。

由AB=10，得A（-5，0），B（5，0），连结PB.

∵P在半圆上，∴PA⊥PB.

Rt△PAB中，sinα=，∴PB=ABsinα=8，PA==6.

设以A、B为焦点，且过点P的椭圆方程为=1（a＞b＞0）

则2a=PA+PB=14，2c=10， ∴a=7，c=5，b²=24.

∴所求椭圆方程为=1.

21.解：依题意，直线AB的方程是即2x+3y-6=0.设则P点到直线AB的距离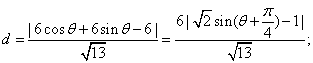

；

点P的坐标为

22. 解：由题意知：双曲线C的方程为=1

设PF₁=m，PF₂=n，∠F₁PF₂=θ，则F₁（-5，0），F₂（5，0）.

∴PF₁-PF₂=m-n=6，m·n=32，F₁F₂=10，

ΔPF₁F₂中，由余弦定理得：

10²=m²+n²-2mncosθ

又m²+n²=（m-n）²+2mn

∴（m-n）²+2mn（1-cosθ）=100

∴cosθ=0　　　∵0＜θ＜π

∴θ=，即∠F₁PF₂=.