高中学生学科素质训练

高二数学测试题—平面与平面的位置关系（3）

一、选择题：（本大题共10小题，每小题5分，共50分）

1．过正方形ABCD的顶点A作线段AP⊥平面ABCD，且AP=AB，则平面ABP与平面CDP所成的二面角的度数是　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．30°　　　　　　　　　 B．45°　　　　　　　　　 C．60°　　　　　　　　　 D．90°

2．已知E、F分别是正方体ABCD—A₁B₁C₁D₁的棱BC，CC₁的中点，则截面AEFD₁与底面ABCD所成二面角的正弦值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　

　　　 C．　　　　　　　　　 D．

3．在四面体ABCD中、已知棱AC的长为，其余各棱长都为1，则二面角A—CD—B的余弦值为　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　　　　　B．　　　　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　　　 D．

4．在空间，下列命题中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．若两直线a,b与直线l所成的角相等，那么a∥b

　　　 B．若两直线a,b与平面所成的角相等，那么a∥b

　　　 C．如果直线l与两平面，所成的角都是直角，那么

　　　 D．若平面与两平面 所成的二面角都是直二面角，那么

5．在下列条件中，可判定平面与平面平行的是　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．、都垂直于平面

　　　 B．内不共线的三个点到的距离相等

　　　 C．l、m是内两条直线，且l∥，m∥

　　　 D．l、m是两异面直线且l∥，m∥，且l∥，m∥

6．若直线a,b是不互相垂直的异面直线，平面则这样的平面、（　　）

　　　 A．只有一对　　　　　　B．有两对　　　　　　　　C．有无数对　　　　　　D．不存在

7．已知二面角到平面的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　　　 B．1　　　　　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　　 D．

8．在直二面角棱AB上取一点P，过P分别在平面内作与棱成45°角的斜线PC、PD，则∠CPD的大小是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．45°　　　　　　　　　　　　　　　　　　　　　　　　　B．60°　　　　　　　　　

　　　 C．120°　　　　　　　　　　　　　　　　　　　　　　　　 D．60°或120°

9．线段AB的两端在直二面角的两个面内，并与这两个面都成30°角，则异面直线AB与CD所成的角是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．30°　　　　　　　　　　　　　　　　　　　　　　　　　B．45°　　　　　　　　　

　　　 C．60°　　　　　　　　　　　　　　　　　　　　　　　　　D．75°

10．平面　　　 （　　）

　　　 A．充要条件　　　　　　　　　　　　　　　　　　　　　 B．充分不必要条件

　　　 C．必要不充分条件　　　　　　　　　　　　　　　　 D．既不充分又不必要条件

二、填空题（本大题共4小题，每小题6分，共24分）

11．Rt△ABC的斜边在平面α内，直角顶点C是α外一点，AC、BC与α所成角分别为30°和45°，

则平面ABC与α所成角为　　　　　　　  .

12．成30°角，则a、b间的距离为　　　　　　　　   .

13．△ABC的三边长分别是3,4,5，P为△ABC所在平面外一点，它到三边的距离都等于2,则P到平面的距离为 　　　　　　　　 .

14．已知、是两个平面，直线若以①　②　③中的两个为条件，另一个为结论，则能构成正确命题的是　　　　　　　   .

三、解答题（本大题共6题，共76分）

15．

　　求证：（12分）

16．设△ABC内接于⊙O，其中AB为⊙O的直径，PA⊥平面ABC。

如图求直线PB和平面PAC所成角的大小.(12分)

17．如图，在正方体ABCD—A₁B₁C₁D₁中，已知P，Q，R，S分别为棱A₁D₁，A₁B₁，AB，BB₁的中点，求证：平面PQS⊥平面B₁RC.(12分)

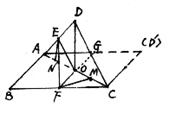
18．把正方形ABCD沿对角线AC折成直二面角B—AC—D，E、F分别为AD、BC的中点，O为正方形的中心，求折起后∠EOF的大小。（12分）

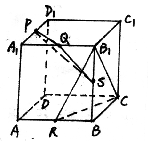
19．如图，正方体AC₁中，已知O为AC与BD的交点，M为DD₁的中点。

（1）求异面直线B₁O与AM所成角的大小。

（2）求二面角B₁—MA—C的正切值。（14分）

20．在正方体AC₁中，E为BC中点（1）求证：BD₁∥平面C₁DE；

（2）在棱CC₁上求一点P，使平面A₁B₁P⊥平面C₁DE；

（3）求二面角B—C₁D—E的余弦值。（14分）

高二数学参考答案

（三）平面与平面的位置关系

一、选择题

1．B　2．C　3．C　4．C　5．D　6．C　7．D　8．D　9．B　10．A

二、填空题

11．60°　　 12．6cm　　　13．　　14．①②③或①③②

三、解答题

15．证明：过b点作平面与α相交于b′

16．解：

17．证明：连结BC₁交B₁C于O，则O为BC₁的中点

连结RO，AC₁，∵R是AB的中点　∴RO∥AC₁

∵P,Q分别为A₁D₁，A₁B₁的中点，易知A₁C₁⊥PQ

∴AC₁⊥PQ（三垂线定理）

18．证明：过F作FM⊥AC于M，过E作EN⊥AC于N，则M，N分别为OC、AO的中点

19．（1）

方法二：取AD中点N，连结A₁N，则A₁N是B₁O在侧面ADD₁A₁上的射影.

易证AM⊥A₁N

∴AM⊥B₁O（三垂线定理）

（2）连结MB₁，AB₁，MC，过O作OH⊥AM于H点，连结B₁H，

∵B₁O平面MAC，∴∠B₁HO就是所求二面角B₁—MA—C的平面角.

20．证