福州侨中05～06学年第二学期期中高二数学复习练习
班级： __________姓名： _______________座号：__________
一、选择题：
1、 下面四个条件中，能确定一个平面的是（ ）
A、 空间中任意四点 B、 空间中两条直线 C、一条直线和一个点 D、两条平行直线
2、已知A、B、C三点不共线，对平面ABC外的任意一点O，下列条件中能确定的M与点A、B、C一定共面的是（ ）
A、
B、 
C、
D、
3、两条异面直线在同一平面内的射影是（ ）
A、两条相交直线 B、两条平行直线 C、两条平行和相交直线 D、不能确定
4、设
，
，且
等于（ ）
A、9 B、
C、
D、
5、已知
，则与
垂直的单位向量是（ ）
A、
B、
C、（1，0 ，0） D、（1，1，1）
6、如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
，那么这条斜线与平面所成的角是（ ）
A、
B、
C、
D、
7、设M是
的重心，记
，则
（ ）
A、
B、
C、
D、
8、已知不重合的两条直线
，给出下面四个命题：
① 
② 
③ 
④ 
其中真命题的是（ ）
A、①② B、①③ C、②③ D、①②④
9、下列命题中，假命题的是（ ）
A、 如果平面
内有两条相交线与平面
内的两条相交线对应平行，则//；
B、 空间一点P位于平面MAB内的充要条件是存在有序实数对
，对空间任一定点
有
；
C、 如果平面内有无数条直线都与平面平行，则//；
D、 若点P是线段AB的中点，则P，A，B满足向量表示式
；
10、正方体
中，E为
的中点，则直线CE垂直于（ ）
A、AC B、BD C、
D、
11、
是所在平面外一点，到三边的距离相等，
于
， 
在内，则是的（ ）
A、外心 B、内心 C、重心 D、垂心
12、空间四边形ABCD中，AC
BD，且AC=BD，E，F，G，H分别是AB，BC，CD，DA的中点，则四边形EFGH是（ ）
A、菱形 B、矩形 C、梯形 D、正方形
二、填空题
13、如果PO、PA分别是平面的垂线、斜线，OA是PA在内的射影，
OA，则由三垂线定理得_____________.
14、已知
的坐标与线段MN中点的坐标分别是______________.
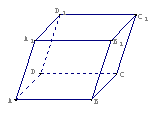15、如图所示，四棱柱
为正方形，侧棱与底面边长均为
，则侧棱
的距离是
16、有一山坡，其倾斜角为，如在斜坡上沿一条与坡底线成的道上山，每向上升高
三、解答题
17、已知直三棱柱
中，
，
的中点，求证：
18、已知
。
19、如图，已知三棱柱在空间坐标系中，
，其中
。（1）证明：是正三棱柱；（2）若
，求直线
与平面
所成角的大小
20、已知矩形
，
外一点，且
分别为
上的点，且
，
成定比1，求满足
的实数
。
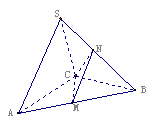21、在三棱锥
的正三角形，平面
M、N分别为
的中点（1）证明：
；（2）求二面角
的大小；（3）求点B到平面CMN的距离。
22、如图，已知四棱锥
的底面为直角梯形，
∥
，且
的中点。（1）证明：
；（2）求
所成的角；（3）求面
所成的角。
04—05学年第二学期期中考高二数学复习练习答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | D | A | B | B | D | A | C | B | B | D |
二、填空题
13、
； 14、
; 15、a;
16、
;
三、解答题（每小题8分，共48分）
17、解：连结
，在
中，
所以
。
，
∽
于是 
在平面
上的射影
（三垂线定理）
18、已知。
解：
=
19、
（1）证明：
，
是正三棱柱
（2）解：
，
直线与平面所成角为
。
20.解：
21.（1）证明：
，则
，
（三垂线定理）
（2）取
∥
。
过
，则
（三垂线定理）
的平面角。
在直角三角形
中，
，
。
，
。
（3）
的距离，且
22(1)
(2)建立空间直角坐标系A-xyz
则A(0,0,0) C(1,1,0) P(0,0,1) B(0,2,0)
(3)
