潮阳棉城中学2005年度第一学期期末考试试卷
高二数学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共150分.
第Ⅰ卷(选择题共60分)
一、选择题(每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目
要求的.)
1.命题“若![]() ,则
,则![]() ”的逆否命题为( )
”的逆否命题为( )
A.若![]() ,则
,则![]() . B.若
. B.若![]() ,则
,则![]() .
.
C.若![]() ,则
,则![]() .
D.若
.
D.若![]() ,则
,则![]() .
.
2.抛物线![]() 的焦点坐标是( )
的焦点坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.命题![]() :存在实数
:存在实数![]() ,使方程
,使方程![]() 有实数根,则“非
有实数根,则“非![]() ”形式的命题是( )
”形式的命题是( )
A.存在实数![]() ,使得方程
,使得方程![]() 无实根.
无实根.
B.不存在实数![]() ,使得方程
,使得方程![]() 有实根.
有实根.
C.对任意的实数![]() ,使得方程
,使得方程![]() 有实根.
有实根.
D.至多有一个实数![]() ,使得方程
,使得方程![]() 有实根.
有实根.
4. 顶点在原点,坐标轴为对称轴的抛物线过点![]() ,则它的方程是( )
,则它的方程是( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]()
5.函数![]() 的导数是( )
的导数是( )
A.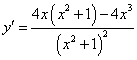 B.
B.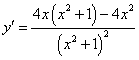
C.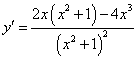 D.
D.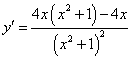
6.若椭圆![]() 上一点P到焦点F1的距离等于6,则点P到另一个焦点F2的距离是( )
上一点P到焦点F1的距离等于6,则点P到另一个焦点F2的距离是( )
A.4 B.
7.![]() 是三个集合,那么“
是三个集合,那么“![]() ”是“
”是“![]() ”成立的( )
”成立的( )
A.充分非必要条件. B.必要非充分条件.
C.充要条件. D.既非充分也非必要条件.
8.已知:点![]() 与抛物线
与抛物线![]() 的焦点的距离是5,则
的焦点的距离是5,则![]() 的值是( )
的值是( )
A.2 B.
9.函数![]() 的单调递减区间是( )
的单调递减区间是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]()
10.抛物线![]() 上的点
上的点![]() 到抛物线焦点的距离为3,则y0=( )
到抛物线焦点的距离为3,则y0=( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
11.以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
 12.已知函数
12.已知函数![]() 的导函数的图象如图甲所示,
的导函数的图象如图甲所示,
则![]() 的图象可能是( )
的图象可能是( )
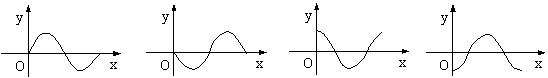 |
A B C D
第Ⅱ卷(非选择题共90分)
二、填空题(每小题6分,共30分.)
13.用符号“![]() ”与“
”与“![]() ”表示含有量词的命题:
”表示含有量词的命题:
(1)实数的平方大于等于0. ______________________.
(2)存在一对实数,使2x+3y+3>0成立.______________________.
14.离心率![]() ,一条准线为
,一条准线为![]() 的椭圆的标准方程是______________________.
的椭圆的标准方程是______________________.
15.曲线![]() 在点(1,1)处的切线方程为___ _______.
在点(1,1)处的切线方程为___ _______.
16.若直线![]() 过抛物线
过抛物线![]() 的焦点,并且与
的焦点,并且与![]() 轴垂直,若
轴垂直,若![]() 被抛物线截得的线段长为4,则
被抛物线截得的线段长为4,则![]() ___ _______.
___ _______.
17. 过双曲线![]() 的右焦点
的右焦点![]() 有一条弦
有一条弦![]() ,
,![]() ,
,![]() 是左焦点,那么
是左焦点,那么![]() 的周长为___ _______.
的周长为___ _______.
三、解答题(共60分)
18.已知命题![]() :“若
:“若![]() 则二次方程
则二次方程![]() 没有实根”.
没有实根”.
(1)写出命题![]() 的否命题;(4分)
的否命题;(4分)
(2)判断命题![]() 的否命题的真假, 并证明你的结论.(6分)
的否命题的真假, 并证明你的结论.(6分)
19.已知双曲线的一条渐近线方程是![]() ,若双曲线经过点
,若双曲线经过点![]() ,求双曲线的标准方程.(12分)
,求双曲线的标准方程.(12分)
20.已知直线![]() 与曲线
与曲线![]() 切于点(1,3),求
切于点(1,3),求![]() 和
和![]() 的值.(14分)
的值.(14分)
21.求![]() 的单调区间和极值.(10分)
的单调区间和极值.(10分)
22.一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成,如图所示.一辆卡车
运载一个长方形的集装箱,此箱平放在车上与车同宽,车与箱的高度共计4.2米,箱宽3
 米,若要求通过隧道时,车体不得超过中线.
米,若要求通过隧道时,车体不得超过中线.
试问这辆卡车是否能通过此隧道,请说明理由.
(14分)
2005年度第一学期高二文科数学期末考参考答案
一、选择题(每小题5分,共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | D | B | B | A | D | A | B | D | B | D | D |
二、填空题(每小题6分,共30分)
13.(1)![]() (2)
(2)![]() 14.
14.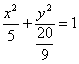
15. ![]() 16. 4 17.
16. 4 17.![]()
三、解答题(共60分.)
18.已知命题![]() :“若
:“若![]() 则二次方程
则二次方程![]() 没有实根”.
没有实根”.
(1)写出命题![]() 的否命题;(4分)
的否命题;(4分)
(2)判断命题![]() 的否命题的真假, 并证明你的结论.(6分)
的否命题的真假, 并证明你的结论.(6分)
18.解:(1)命题![]() 的否命题为:“若
的否命题为:“若![]() 则二次方程
则二次方程![]() 有实根”.
有实根”.
(2)命题![]() 的否命题是真命题.
的否命题是真命题.
证明:![]()
![]() 二次方程
二次方程![]() 有实根.
有实根.
∴该命题是真命题.
19.已知双曲线的一条渐近线方程是![]() ,若双曲线经过点
,若双曲线经过点![]() ,求双曲线的标准方程.(12分)
,求双曲线的标准方程.(12分)
解:由已知可知双曲线的两条渐近线为![]()
因此可设所求双曲线为![]() (6分)
(6分)
将![]() 代入
代入![]() ,解得
,解得![]() (4分)
(4分)
∴双曲线方程为![]()
∴标准方程为:![]() (2分)
(2分)
20.已知直线![]() 与曲线
与曲线![]() 切于点(1,3),求
切于点(1,3),求![]() 和
和![]() 的值.(14分)
的值.(14分)
解:∵直线![]() 与曲线
与曲线![]() 切于点(1,3)
切于点(1,3)
∴点(1,3)在直线![]() 与曲线
与曲线![]() 上 (2分)
上 (2分)
∴![]()
![]() (4分)
(4分)
又由![]() (4分)
(4分)
由导数的几何意义可知:![]() (2分)
(2分)
将![]() 代入
代入![]() ,解得
,解得![]() (2分)
(2分)
21.求![]() 的单调区间和极值.(10分)
的单调区间和极值.(10分)
解:![]() (2分)
(2分)
令![]() ,即
,即![]() ,解得
,解得![]() (2分)
(2分)
当![]() 时,即
时,即![]() ,解得
,解得![]() ,
,
函数![]() 单调递增;
(2分)
单调递增;
(2分)
当![]() 时,即
时,即![]() ,解得
,解得![]() ,
,
函数![]() 单调递减;
(2分)
单调递减;
(2分)
综上所述,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;当
;当![]() 时取得极大值
时取得极大值![]() ,当
,当![]() 时取得极小值
时取得极小值![]() 。
。
(2分)
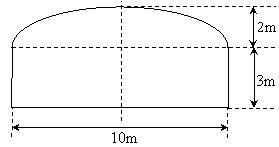
22.一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成,如图所示.一辆卡
车运载一个长方形的集装箱,此箱平放在车上与车同宽,车与箱的高度共计4.2米,
箱宽3米,若要求通过隧道时,车体不得超过中线.
试问这辆卡车是否能通过此隧道,请说明理由.(14分)
 |
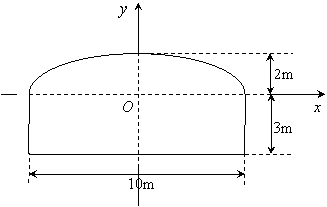
解:建立如图所示的坐标系, (4分)
则此隧道横截面的椭圆上半部分方程为:![]() .
(4分)
.
(4分)
令![]() ,则代入椭圆方程,解得
,则代入椭圆方程,解得![]() ,因为
,因为![]() ,
(5分)
,
(5分)
所以,卡车能够通过此隧道. (1分)
 |