高二数学同步测试—空间向量(6)
一.选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
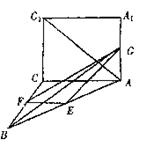
1.平行六面体 ![]() 中,E,F,G,H,P,Q是
中,E,F,G,H,P,Q是![]() 的中点,则有关系 ( )
的中点,则有关系 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知空间三点O(0,0, 0), A(-1, 1, 0), B(0, 1, 1), 在直线OA上有一点H满足BH⊥OA,则点H的坐标为 ( )
A.(-2, 2, 0) B.(2, -2, 0) C.![]() D.
D.![]()
3.若![]() 则
则 是
是![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.在棱长为1的正四面体ABCD中,E, F分别是 BC, AD的中点,则![]() ( )
( )
A. 0
B. ![]() C.
C. ![]() D.
D. ![]()
5.O是平面上一 定点,A、B、C是平面上不共线的三个点,动点P满足
![]() 则P的轨迹一定通过△ABC的 ( )
则P的轨迹一定通过△ABC的 ( )
A.外心 B.内心 C.重心 D.垂心
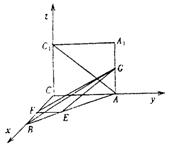
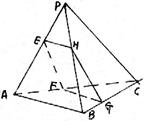
6.如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①![]() ;
;
②![]() ;
;
③三棱锥D—ABC是正三棱锥;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确的是 ( )
A.①② B.②③ C.③④ D.①④
7. 若![]() ,
, ![]()
![]() , 则
, 则![]() = ( )
= ( )
A. 4 B. 15 C. 7 D. 3
 8. 三棱柱
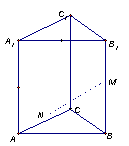
8. 三棱柱![]() 中,M、N分别是
中,M、N分别是![]() 、
、![]() 的中点,设
的中点,设![]() ,
,![]() ,
,![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.设![]() ={1,2,0},
={1,2,0}, ![]() ={1,0,1},则:“
={1,0,1},则:“![]() ={
={![]() ,-
,-![]() ,-
,-![]() }”是“
}”是“![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() 为单位向量”的 ( )
为单位向量”的 ( )
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既非充分条件也非必要条件
10.给出下列四个结论:
①若平面α内两条直线与平面![]() 内两条直线分别平行,则α∥
内两条直线分别平行,则α∥![]() ;
;
②过直线外一点能作一条直线与已知直线平行;
③如果一个角的两边分别平行于另一个角的两边,那么,这两个角相等;
④若![]() ,则A,B,C三点共线.
,则A,B,C三点共线.
其中恒成立的是 ( )
A.①② B.②③ C.③④ D.②④
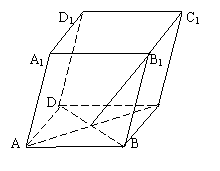 11.如图,在平行六面体ABCD–A1B1C1D1中,M为AC
11.如图,在平行六面体ABCD–A1B1C1D1中,M为AC
与BD的交点.若![]() ,
,![]() ,
,![]() ,则下列
,则下列
向量中与![]() 相等的向量是
( )
相等的向量是
( )
| |
C.![]() D.
D.![]()
12.如图,正三棱锥P-ABC的底面边长为1,
E,F,G,H,分别是PA,AC,BC,PD的中点,四边形EFGH
的面积为S(x),则S(x)值域为 ( )
A. {![]() } B.(0, +∞) C . (
} B.(0, +∞) C . (![]() , +∞) D.(
, +∞) D.(![]() , +∞)
, +∞)
二、填空题(本大题共4小题,每小题6分,共24分)
13. 已知![]() =(—4,2,x),
=(—4,2,x),![]() =(2,1,3),且
=(2,1,3),且![]() ⊥
⊥![]() ,则x= .
,则x= .
14. 向量![]() ,
,![]() ,则
,则![]() 和
和![]() 所夹角是 .
所夹角是 .
15. 已知A(1, 0, 0), B(0, 1, 0 ), C(0, 0, 1), 点D满足条件:DB⊥AC, DC⊥AB,
AD=BC, 则D的坐标为 .
16. 设![]() 是直线,
是直线,![]() 是平面,
是平面,![]() ,向量
,向量![]() 在
在![]() 上,向量
上,向量![]() 在
在![]() 上,
上,![]() ,则
,则![]() 所成二面角中较小的一个的大小为
.
所成二面角中较小的一个的大小为
.
三、解答题(本大题满分74分)
17.(10分)已知向量![]() 满足
满足![]() ,
, ![]() .
.
求![]() .
.
18.(12分) 给定⊿ABC,对空间中的一点P,建立如下变换f:AP的中点为Q, BQ的中点为R, CR的中点为P′, f(P)=P′,则对于变换f,是否存在不动点(即P与P′重合的点)?
19.(12分)正方形ABCD,ABEF的边长都是1,且平面ABCD,ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a (0<a<![]() ), 求当MN的长最小时,面MNA与面MNB所成的二面角
), 求当MN的长最小时,面MNA与面MNB所成的二面角![]() 的大小.
的大小.
 20.(12分)
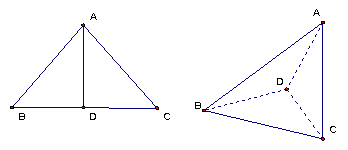
如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成的角的
20.(12分)
如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成的角的
大小为![]() ,求四面体ABCD的体积.
,求四面体ABCD的体积.
|
直,∠ACB=90°,E、F分别是AB、BC的中点,
G是AA1上的点.
![]()
![]() (1)若AC1⊥EG,试确定点G的位置;
(1)若AC1⊥EG,试确定点G的位置;
(2)在满足条件(1)的情况下,
![]()
![]() 试求cos<AC,GF>的值.
试求cos<AC,GF>的值.
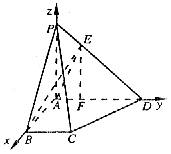 22.(14分) 在四棱锥P—ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角,AE⊥PD,垂足为E。建立空间直角坐标系A-xyz,如图。
22.(14分) 在四棱锥P—ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角,AE⊥PD,垂足为E。建立空间直角坐标系A-xyz,如图。
(1)证明BE⊥PD;
(2)求异面直线AE与CD所成的角;
(3)设n=(1,p,q),满足n⊥平面PCD,求n的坐标.
高二数学(六)参考答案
一、选择题
1.A 2.C 3.A 4.D 5.B 6.B 7.D 8.D 9.B 10.D 11.A 12.C
2.解:设![]() 以
以![]() 为基底,则
为基底,则
![]()
所以![]() .选A.
.选A.
3.解:设![]() , 易知
, 易知![]() . 即条件具有充分性.
. 即条件具有充分性.
又若![]() 时,
时,![]() ,虽有
,虽有![]() ,但条件
,但条件![]() 显然不成立,所以条件不具有必然性.
显然不成立,所以条件不具有必然性.
4.解:![]()
![]() =
=
=![]()
=![]() =
=![]() .选D.
.选D.
12.解:当顶点P与底面正⊿ABC重心很接近时,矩形EFGH的面积较小;重合时矩形的面积为![]() 选C.
选C.
二、填空题
13. 2 14.60° 15.(1,1,1)或![]() 16.
16.![]()
14.解:由![]() ,
, ![]() ,
,
有![]()
![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
, 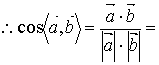
![]() .
.
15解:设D(x, y, z), 则![]() ,
,![]()
![]() (x-1, y, z),
(x-1, y, z),
![]() (-1, 0, 1),
(-1, 0, 1), ![]() (-1,1, 0),
(-1,1, 0), ![]() (0, -1, 1). 又DB⊥AC
(0, -1, 1). 又DB⊥AC![]() -x+z=0,
-x+z=0,
DC⊥AB![]() -x+y=0,
AD=BC
-x+y=0,
AD=BC![]()
![]()
联立解得x=y=z=1或x=y=z=![]() 所以D点为(1,1,1)或
所以D点为(1,1,1)或![]() .
.
三、解答题
17.解:![]()
得![]() =
=![]()
18.解:由已知,有![]() 且
且![]()
![]() .要使P′,P重合,应有
.要使P′,P重合,应有
![]()
![]() ,
,![]() .
.
∴符合条件的不动点存在.
19.解:如图 建立空间直角坐标系,则B(0,0,0), A(1,0,0), M![]()
N![]()
![]()
![]() (0<a<
(0<a<![]() ),
),
∴当a=![]() ,即M,N分别是AC,BF的中点时,MN最小,此时,M
,即M,N分别是AC,BF的中点时,MN最小,此时,M![]()
 MN的中点G
MN的中点G![]()
![]()
![]() 则
则![]()
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
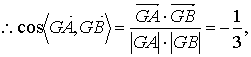 故所求二面角
故所求二面角![]() =arccos
=arccos![]() .
.
20.解法一:如图建立空间直角坐标系,
 由题意,有
由题意,有![]() ,
,![]() ,
,![]() .
.
设D点的坐标为![]()
![]() ,
,
则![]() ,
,![]()
则![]() ,
,
| |
∴![]() , 得
, 得![]() ,故BD的长度是4,
,故BD的长度是4,
又![]() , 因此四面体ABCD的体积是
, 因此四面体ABCD的体积是![]() ,
,
解法二:过A引BE的平行线,交CB的延长线于F,∠DAF是异面直线BE与AD所成的角.
 ∴∠DAF=
∴∠DAF=![]() ,
,
∵E是AC的中点,∴B是CF的中点, AF=2BE=![]() .
.
又BF,BA分别是DF,DA的射影,且BF=BC=BA, ∴DF=DA
三角形ADF是等腰三角形,
AD=![]() , 故
, 故 ![]() ,
,
|
21.解:(1)由正方形ACC1A1与等腰直角△ACB互相
垂直,∠ACB=90°,∴BC⊥AC,∴BC⊥CC1.以C
为坐标原点,建立空间直角坐标系C—xyz,如图.
设AC=CB=a,AG=x,则A(0,a,0).
C1(0,0,a),G(0,a,x),E(-![]() ,
,![]() ,0).
,0).
![]()
![]() AC1=(0,-a,a),EG=(-
AC1=(0,-a,a),EG=(-![]() ,
,![]() ,x).
,x).
![]()
![]() ∵AC1·EG=0,∴-
∵AC1·EG=0,∴-![]() +xa=0. ∴x=
+xa=0. ∴x=![]() ,∴G为AA1的中点.
,∴G为AA1的中点.
(2)∵G(0,a,![]() ),F(
),F(![]() ,0,0),
,0,0),
![]()
![]() ∴GF=(
∴GF=(![]() ,-a,-
,-a,-![]() ),AC1=(0,-a,a).(9分)
),AC1=(0,-a,a).(9分)
![]()
![]()
![]()
![]() ∴ GF =
∴ GF =![]() a, AC1 =
a, AC1 =![]() a,∴GF·AC1=a2-
a,∴GF·AC1=a2-![]() =
=![]() .
.
![]()
![]() ∴cos<AC1,GF>=
∴cos<AC1,GF>=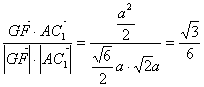 .
.
22.解:由已知,得A(0, 0, 0), B(a, 0, 0), C(a, a, 0), D(0, 2a, 0).
∵PA⊥面ABCD,PD与面ABCD成30°,
∴∠PDA=30°,
∴P(0, 0, ![]() a).
a).
过E作EF⊥AD,垂足为F,则AE=a,∠EAF=60°,AF=![]() a,EF=
a,EF=![]() a.
a.
 ∴E(0,
∴E(0, ![]() a,
a, ![]() a) .
a) .
![]() (1)BE=(﹣a,
(1)BE=(﹣a,![]() a,
a, ![]() a),
a),
![]() PD=(0, 2a,,﹣
PD=(0, 2a,,﹣![]() a),
a),
![]()
![]() ∴BE·PD=
∴BE·PD=![]() a·2a+
a·2a+![]() a·(﹣
a·(﹣![]() a) =0,
a) =0,
∴BE⊥PD.
![]()
![]() (2)AE=(0,
(2)AE=(0,![]() a,
a, ![]() a),CD=(﹣a,a,0),
a),CD=(﹣a,a,0),
![]()
![]() ∴cos<AE, CD> =
∴cos<AE, CD> =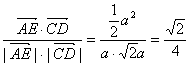 .
.
∴异面直线AE与CD所成的角为arccos![]() .
.
![]()
![]() (3)∵n⊥平面PCD,∴n⊥PD,n⊥CD,
(3)∵n⊥平面PCD,∴n⊥PD,n⊥CD,
![]()
![]() 又n=(1,p,q), PD=(2, 2a, ﹣
又n=(1,p,q), PD=(2, 2a, ﹣![]() a), CD=(﹣a, a, 0),
a), CD=(﹣a, a, 0),
![]() ∴n·PD=0·1+2a·p-
∴n·PD=0·1+2a·p-![]()
![]() a·q=0,
a·q=0,
![]() n·CD=1·(﹣a)+a·p+q·0=0,
n·CD=1·(﹣a)+a·p+q·0=0,
![]()
![]() 即 p-
即 p-![]() q=0 ∴ p=1
q=0 ∴ p=1
p-1=0
q=![]() ,
,
即n的坐标为(1, 1, ![]() ).
).