仪 征 电 大 附 中
高二年级十二月月考数学试卷
2005.12
一、选择题(每小题5分,共60分)
1、若直线过点![]() ,且倾斜角为
,且倾斜角为![]() ,则直线的方程为( )
,则直线的方程为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.两定点A(-2,-1),B(2,-1),动点P在抛物线![]() 上移动,则△PAB重
上移动,则△PAB重
心G的轨迹方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、直线x – 2y +2 = 0与直线3x – y + 7 = 0的夹角等于 ( )
A![]() .
B
.
B![]() . C
. C ![]() . D arctan7.
. D arctan7.
4.参数方程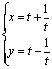
![]() 表示曲线的离心率为( ) A.
表示曲线的离心率为( ) A.![]() B.
B.![]() C.
C.![]() D.2
D.2
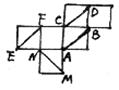 5.右图是一个正方体的展开图,在原正方体中,有下列命题:
5.右图是一个正方体的展开图,在原正方体中,有下列命题:
①AB与CD所在直线垂直; ②CD与EF所在直线平行
③AB与MN所在直线成60°角; ④MN与EF所在直线异面
其中正确命题的序号是( )
A.①③ B.①④ C.②③ D.③④
6.已知A(1,2)和B(3,—4)在直线![]() 的同侧,则k的取值范围是( )
的同侧,则k的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知椭圆的中心在原点,离心率![]() ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线![]() 的
的
焦点重合,则此椭圆方程为 ( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.如果方程x 2+ky 2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A.(0, +∞) B.(0, 2) C.(1, +∞) D.(0, 1)
9.直线y = x +1被椭圆x 2+2y 2=4所截得的弦的中点坐标是 ( )
A.(![]() , -
, -![]() ) B..(-
) B..(-![]() ,
, ![]() ) C.(
) C.(![]() , -
, -![]() ) D.(-
) D.(-![]() ,
,![]() )
)
10.一动圆与两圆:x2+y 2=1和x2+y 2-8x+12=0都外切,则动圆心的轨迹为 ( )
A.抛物线 B.圆 C.双曲线的一支 D.椭圆
11.过点(2,—2)且与![]() 有相同渐近线的双曲线方程是( )
有相同渐近线的双曲线方程是( )
A.![]() B.
B.
![]() C.
C.![]() D.
D.
![]()
12.直线![]() 与抛物线
与抛物线![]() 交于A、B两点,O为原点,则△AOB是( )
交于A、B两点,O为原点,则△AOB是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.其形状不能确定
二、填空题(每空4分,共16分)
13.以点(-2,3)为圆心且与y轴相切的圆的方程是 .
14.若![]() >0, b >0,则
>0, b >0,则![]() 的最小值是
.
的最小值是
.
15、椭圆![]() 的一个焦点为(0,2),那么k=____________。
的一个焦点为(0,2),那么k=____________。
16.设![]() 满足约束条件:
满足约束条件: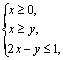 则
则![]() 的最大值是
.
的最大值是
.
三、解答题
17.已知圆C:![]() ,直线L:(2m+1)x+(m+1)y-7m-4=0(m∈R)。(Ⅰ)求证不论m取什么实数,直线恒与圆相交于两点。(Ⅱ)求直线L被圆C截得的弦长最小时的直线方程。(12分)
,直线L:(2m+1)x+(m+1)y-7m-4=0(m∈R)。(Ⅰ)求证不论m取什么实数,直线恒与圆相交于两点。(Ⅱ)求直线L被圆C截得的弦长最小时的直线方程。(12分)
18. 已知抛物线![]() ,焦点为F,顶点为O,点P在抛物线上移动,
,焦点为F,顶点为O,点P在抛物线上移动,
Q是OP的中点,M是FQ的中点,求点M的轨迹方程。(12分)
19、某厂生产甲、乙两种产品,甲种产品每件需![]() 种原料8克,
种原料8克,![]() 种原料24克,每件利润60元;乙种产品每件需
种原料24克,每件利润60元;乙种产品每件需![]() 种原料和
种原料和![]() 种原料各16克,每件利润80元.现有
种原料各16克,每件利润80元.现有![]() 种原料2400克,
种原料2400克,![]() 种原料2880克,问甲、乙两产品各生产多少件,工厂可获得最大利润(原料不再外购,产品可完全售出)。(12分)
种原料2880克,问甲、乙两产品各生产多少件,工厂可获得最大利润(原料不再外购,产品可完全售出)。(12分)
20.是否存在同时满足下列两个条件的椭圆:
(1)中心在作坐原点O,焦点F1、F2在![]() 轴上且长轴为4;
轴上且长轴为4;
(2)PF1、PO、PF2成等比数列,其中P是椭圆上一点且PO=![]() 。
。
如果存在,求出该椭圆方程;如果不存在,说明理由。(12分)
21.在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,EF=![]() ,求AD与BC所成角的大小。(12分)
,求AD与BC所成角的大小。(12分)
|
(1)求证:MN是AB和PC的公垂线
(2)求异面二直线AB和PC之间的距离(14分)
仪 征 电 大 附 中
高二年级十二月月考数学答卷纸
得分___________
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | B | B | C | D | B | C | D | B | C | B | B |
13、![]() , 14、4
, 14、4
15、1 16、5
17、(1)因L恒过点![]() ,而点
,而点![]() 在圆C内部;
在圆C内部;
(2) y=2x-5
18、![]()
19、甲30件,乙135件,最大利润12600元
20、存在,方程为![]()
21、![]()
22、(1)略
(2)![]()
